Communication complexity assignment 2
- The communication protocol can be formally defined as
fA: (∏<i,X) -> {0,1}, i mod 2==0
fB: (∏<i,Y) -> {0,1}, i mod 2==1
where ∏<i is the history of all messages communicated so far. This can be represent as a binary tree where the first depth represents Alice’s communication, the second Bob’s, the third Alice’s, the fourth Bob’s and so on. For the communication complexity of identity, both A and B must send n bits.
Proof
Let the protocol used have k bits for transmitting n bits where
1<k<n
And X and Y are strings {0,1}n, where k+1 is the parity bit 1 for YES and 0 for NO.
When k=2, n=4, X=1011 and Y=1010, then we end up with the transcript {1,1,0,0,1}. This can be shown using the transcript below:
Sender Bit number A Bit number B Bit Sent Transcript
A 1 1 {1}
B 1 1 {1,1}
A 2 0 {1,1,0}
B 2 0 {1,1,0,0}
K+1 K+1 1 {1,1,0,0,1}
When k=2, n=4, X=1000 and Y=1001, then we end up with then we end up with the transcript {1,1,0,0,1}. This can be shown using the transcript below:
Sender Bit number A Bit number B Bit Sent Transcript
A 1 1 {1}
B 1 1 {1,1}
A 2 0 {1,1,0}
B 2 0 {1,1,0,0}
K+1 K+1 1 {1,1,0,0,1}
Thus for two different string pairs (X,Y), it can be shown that the transcript is the same even though the strings pairs are different.
Proof
Let the protocol used have k bits for transmitting n bits where
1<k<n
And X and Y are strings {0,1}n, where k+1 is the parity bit 1 for YES and 0 for NO.
When k=2, n=4, X=1011 and Y=1010, then we end up with the transcript {1,1,0,0,1}. This can be shown using the transcript below:
Sender Bit number A Bit number B Bit Sent Transcript
A 1 1 {1}
B 1 1 {1,1}
A 2 0 {1,1,0}
B 2 0 {1,1,0,0}
K+1 K+1 1 {1,1,0,0,1}
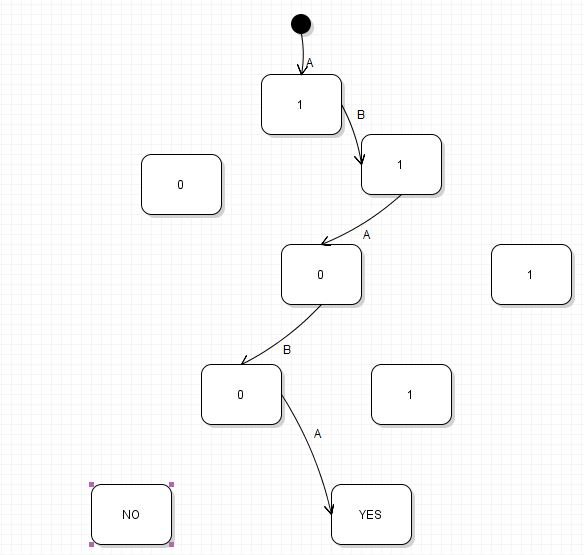
This can be shown using a binary tree as below:
From the transcript and the binary tree, we can see the protocol ends up with the parity bit set to YES meaning the strings A and B match, which is false.
Therefore by contradiction, we can determine we need at least n+1 bits when taking into account the parity bit.
@OriginalWorks
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!