Let's explore a little bit the type system of Ada.

Ada's type system is very important, because Ada is a strongly typed programming language and types define the exact domain of your program: they help you to write better software.

For instance, in the previous article I did the example of the age of a person. If your program works with numbers which are ages of human beings and at a certain point, for whatever reason, the value of an age can become huge or negative (if the age is held into a signed integer variable), usually you must do your explicit checks.

E.g., in C likely you would use assert().

typedef int age;
/* ... */
age x = some_computation();
assert(x >= 0 && x <= 140);

typedef unsigned int age;
/* ... */
age x = some_computation();
assert(x <= 140);

A long contrived example can be found here. We need to call for the assertion each time we read an age from somewhere (external input) and each time we compute the age, for example as a difference between the current age and the year passed since the first kiss.

In Ada we are not limited to say that a type is a signed or unsigned integer, or whatever. We can say a lot more, as we've already seen. In Ada we would write something like this:

subtype Age_Type is Natural range 0 .. 140;
-- ...
X : Age_Type;
-- ...
X := Some_Computation;

And if something goes wrong with the age, so that it acquires a value which can't be an age, we don't need to add explicitly an assertion, since the subtype already defines exactly the values the variable can hold.

When run the C example will output the following (if compiled without having NDEBUG defined, since this definition disables assertions):

a.out: age_madness.c:70: uage_of_kiss: Assertion `(current_age - dist_of_first_kiss) <= max_uage' failed.
Aborted

When compiled with -DNDEBUG, the assertions are disabled and you'll see the problem, thanks to lines printed as debug informations on the standard output.

DEBUG uage of kiss 4294967259
so, you waiting for so long...
DEBUG age of kiss -37
you weren't adult!

When you run the Ada example, the output is:

raised CONSTRAINT_ERROR : test_age_madness.adb:15 range check failed

Even if you nowhere had to write an explicit check on the values.

Writing good software forces you to define the domain of your problem, and Ada has the tools carved into the language to express such a domain. Of course, you should use them, or they would be worthless. For example, you could have

type Age_Type is new Integer;

That is, Age_Type is just an integer… In this case we lose the checks Ada can do for us. So, the best thing to do is to extensively use Ada's type system. In the example I've done we can be more precise: when talking about the “distance”, in years, from an event occurred in my past, or from an event I expect it will occur in my future, this distance can't be any integer number, because my age has a lower limit (when I was born a was 0) and a upper limit (human beings won't long more than 140 years in our take).

Then a number representing the “distance” between ages of a human being, shouldn't be just a signed integer (signed because the sign can tell if we are talking about the past or the future). We could have something like:

subtype Age_Distance is Integer range -Age_Type'Last .. Age_Type'Last;

instead of

subtype Age_Distance is Integer;

Then we can test another feature of Ada's compiler: if it knows a value at runtime, it can check if the statically checkable constraints are in fact satisfied.

With

   -- ...
   subtype Age_Distance is Integer range -Age_Type'Last .. Age_Type'Last;
   -- ...
   function Get_Dist_From_First_Kiss return Age_Distance is (150);
   -- ...

The compiler warns you (and gives compilation error if you use the -gnatwe option):

test_age_madness.adb:10:62: warning: value not in range of type "Age_Distance" defined at line 6
test_age_madness.adb:10:62: warning: "Constraint_Error" will be raised at run time

But the compiler can tell just because in our contrived example we used a constant for Get_Dist_From_First_Kiss.

Now is time to see something more about types. We've seen already something, but there's much more.

Type or subtype, that's the question

The type keyword is used to define a new type. It will be treated exactly as a new type, meaning that you won't be able to mingle it with other types that easily, even if the type you won't to mess with is the “base” from which you defined the new type. This is because for a strongly typed language, those are really two different types, it would be like mixing, say, Integer with String. It can't be done.

C/C++ programmers out there should keep in mind that, unfortunately for these languages, typedef does not define a new type, despite the name. It defines just a synonym.

type Cows_Counter_Type is new Integer;

This line defines a new type, which is really a new type and not a synonym for Integer. That means that Ada don't know how to handle it altogether with a true Integer. The new type inherits operations from the base type Integer, but still they are considered operations on Cows_Counter_Type, not on Integer. So, again, you can't mix them.

   -- ...
   Cows_In_The_Park : Cows_Counter_Type := 0;
   Newborn_Cows     : Integer := 1;
   -- ...
   Cows_In_The_Park := Cows_In_The_Park + Newborn_Cows;
end Test_Types;

This won't compile and will give an error like this:

test_types.adb:8:41: left operand has type "Cows_Counter_Type" defined at line 2
test_types.adb:8:41: right operand has type "Standard.Integer"

We could convert the Newborn_Cows into Cows_In_The_Park:

   Cows_In_The_Park := Cows_In_The_Park + Cows_Counter_Type (Newborn_Cows);

This is feasable, but it could be a sign that you haven't defined your types correctly, i.e., you're “design” of the domain of the problem is poor. The solution in this case is very simple: the number Newborn_Cows is in fact a counter of newborn cows, so its type should be Cows_Counter_Type. (Also, Cows_Counter_Type really should be new Natural, because hardly counting cows gives negative numbers).

Types defined with type are called derived type and it doesn't matter how they are defined (new Another_Type or in other ways we'll see soon): they must be considered types of their own.

On the other hand, subtypes are compatibile with their base type. Age_Type we've seen before is compatible with Natural (which in turn is a subtype of Integer), and so we can do operations like An_Age + 1.

So, subtyping can be used to “restrict” the acceptable values of the “parent” type, as we did for Age_Type.

When you really need a new type, then likely you will also define your operations on it.

Predefined types and subtypes

There are predefined types and subtypes. Reading the standard it seems that implementations have some liberty on the details, but must assure some features. For example, the range of Integer must include the range –2¹⁵+1 .. +2¹⁵–1.

The integer category is child of the elementary, scalar, discrete category, and there exist two other subcategories: signed integer and modular integer. The signed integer should be obvious; the modular integer are those with wrap-around arithmetic.

The two keywords related to these “categories” are range and mod. These are the tools through which integer types can be defined.

In fact the type Integer is something like this:

type Integer is range -2**15+1 .. +2**15-1;

But indeed it is implementation defined (the standard just requires it is at least as large as to contain the range shown above). You can find the definition into the Standard package (implicitly always “included” in your program).

However this shows another greatness of the Ada's type system: you specify exactly what you expect from a type, even one of the “primitive” one! Then the compiler on a specific machine will accomodate the type into whatever the machine has, if it is possible — if it isn't, well, you are out of luck.

Now that we have our “primitive” Integer (which indeed isn't so primitive, and likely it is concretely someway based on an anonymous type), it is easy to define also Natural and Positive as subtypes — in fact we want it easy to mix operations among these types.

subtype Natural  is Integer range 0 .. Integer'Last;
subtype Positive is Integer range 1 .. Integer'Last;

The attribute last gives tha last value a type can have (but likely you already deduced that). Integer operations' arguments are declared as Integer'Base, i.e., they are defined for whichever is the actual type Integer is based on. (This clearly must be machine dependent). The Integer type inherits them, and they also work for subtypes — I've explained above why.

For floating point we have the keyword digits; the Float type is implementation defined, too, and the standard requires a decimal precision of at least 6. Something like this:

type Float is digits 6 range -16#0.FFFF_FF#E+32 .. 16#0.FFFF_FF#E+32;

We specify six digits precision and the range expressed in base 16 — it is easier this way because digital computers are “binary”, and so the mantissa is stored always as nothing but a binary number.

Another predefined type is Character, which is an “enumeration” of characters, according to the single byte standard ISO 8859-1 (aka Latin 1), except that literals for control codes aren't defined.

type Character is (..., ' ', '!', '"', ...);

This looks more like a sort of placeholder to describe partially what Character is, but likely the underlying storage is just a eight-bit byte. A single character can be written using single quotes, but control codes must be written in another way. The attribute Val of Character is what we need:

Escape_Character : constant Character := Character'Val (27);

We have also Wide_Character, which is the type we need when we want to represent the characters defined in ISO 10646 Basic Multilingual Plane; this is another enumerative definition, that is it goes on like:

type Character is (..., list of Unicode characters, ...);

The Wide_Wide_Character isn't restricted to the BMP (Basic Multilingual Plane), but comprehends all the characters defined by ISO 10646. In the Standard package described by Ada Standard (v. 2012) we can see another interesting thing:

for Wide_Wide_Character'Size use 32;

This tells to use a 32 bit “storage” to store the value of the Wide_Wide_Character.

An array of Characters makes a string: another predefined type is in fact String, which is something like:

type String is array (Positive range <>) of Character;

That is, a String is an array of Character, indexed by a positive integer; the “diamond” stands for any range. We must specify what <> actually is when we use the type:

My_String : String (100);

But we have already seen that the compiler can deduce it if we initialize the string. So, the following is ok:

My_String : String := "hello world";

but the following gives error:

My_String : String;

The compiler says:

unconstrained subtype not allowed (need initialization)
provide initial value or explicit array bounds

Strings are made of Characters, so Wide_Strings must be made of Wide_Characters, and Wide_Wide_Strings must be made of Wide_Wide_Characters.

Another standard type is Duration, and this allows us to see another marvel of Ada. In fact Duration is defined like this:

  type Duration is delta 0.000000001
     range -((2 ** 63 - 1) * 0.000000001) ..
           +((2 ** 63 - 1) * 0.000000001);
   for Duration'Small use 0.000000001;

This is the way we can specify a fixed point type. The delta gives the smallest increment possible, and the range part specifies the range; what about the for ... use ... part?

It happens that the smallest value used is approximated by a value which is the inverse of a power of 2 value, and which isn't greater than delta. This is done for performance reason, but you lose precision. In case you don't want to lose precision, you can specify the exact smallest value that must be used. And for Xxx'Small use yyy has this purpose.

Integer numeric types and strings are quite common and you expect those. What about a type for duration? I think this is why: Ada is used in hard realtime systems, and in those systems measuring time is important. Furthermore, Ada has a delay statement which can be used to, well, delay… Usually you use it in tasks, i.e., when you use the concurrecy features of Ada; but if you want to try it, you can uselessly waste some time between a statement and another!

Another standard predefined type is Boolean. Conditions and true/false expressions give a Boolean as a result. This is an enumeration type, like Character, but it has only two possible value, True and False.

type Boolean is (False, True);

In the Standard package there's more; in fact, it is imposed a size of 1 (bit), and exact values are assigned to the enumeration (so that it is true that False < True, as required by the standard):

for Boolean'Size use 1;
for Boolean use (False => 0, True => 1);

Other standard packages may define other types which, being described by the standard, also should be considered as “predefined”. But they are, as said, part of other packages, and you must with these packages in order to use their type. For this reason I won't consider them here.

Now, a raw list of the type predefined in the Standard package, and therefore ready to be used. This list lists types I've described above, plus others I haven't. Not all of these types are mandatory according to the standard, in fact, for example, for the “extra” integer types:

An implementation may provide additional predefined signed integer types, declared in the visible part of Standard, whose first subtypes have names of the form Short_Integer, Long_Integer, Short_Short_Integer, Long_Long_Integer, etc. Different predefined integer types are allowed to have the same base range. However, the range of Integer should be no wider than that of Long_Integer. Similarly, the range of Short_Integer (if provided) should be no wider than Integer.

Nonetheless,

An implementation should support Long_Integer in addition to Integer if the target machine supports 32-bit (or longer) arithmetic.

Without further ado, here the list according to GNAT implementation of Standard suitable for my system:

Boolean
Integer (signed 32 bit on my system)
- Natural
- Positive
Short_Short_Integer (signed 8 bit on my system)
Short_Integer (signed 16 bit on my system)
Long_Integer (as Integer)
Long_Long_Integer (signed 64 bit on my system)
Short_Float (32 bit floating point on my system)
Float (as Short_Float in my system)
Long_Float (64 bit floating point, likely IEEE 754 binary64 on many typical consumer desktop computers)
Long_Long_Float (with a size of 96 bit, which is odd. IEEE 754 has binary128, which isn't anyway supported by any system I am aware of… This number of bits, 96, matches the number of bits used internally, for intermediate results, by some FPUs; it should be the so called extended precision, but it is just 80 bit on x86 family — it was 96 bit on famous Motorola's CPUs, which are very old now)
Character
Wide_Character
Wide_Wide_Character

By the way, these definitions in Standard can be seen by adding the -gnatS option when compiling a source. The Standard package will be written to the standard output.

Seen “building blocks”

The Ada standard manual defines a hierarchy of categories to classify (or should I say categorize?) types Ada can define and for which a hierarchical picture makes sense. We have already seen these “leaves”:

signed integer (range -X .. +Y)
modular integer (mod N), which indeed we have seen in another article; Standard doesn't have any modular integer defined
enumeration (type Enum is (A, B, C, …))
floating point (digits N range A .. Z)
ordinary fixed point (delta N range A .. Z)
array (array (Index_Type range ...), see e.g. String)

There's another one I want to add:

decimal fixed point (delta N digits R, followed by an optional range, and N must be a power of 10)

If you have ever worked in a financial institution with values which represented money, you know very well that you don't use floating point numbers to represent money and do computation “on money”. It is a big no no. Well, Ada has a builtin way of dealing with what should be used in these cases, that is, a decimal fixed point type — with a desidered number of decimal digits and an overall number of digits (and a range, if you need to impose limits different from the one implicit in the type definition).

All these types can be categorized as elementary scalars. In a previous article we've already seen records, which are composite types (we have seen untagged records so far). They are basically what is called struct in C (and in C++ when they aren't classes with default public visibility).

type Person is
   record
      -- ...
   end record;

And there's still a lot more to know about types…!

Source

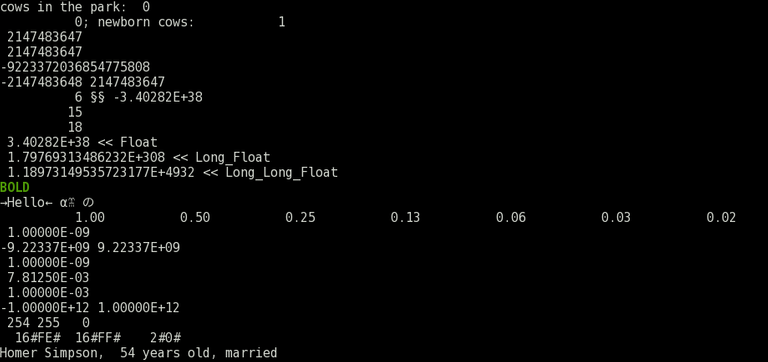
The source test_types.adb plays with several types/subtypes and struggle to output them someway. It contains UTF-8 character in the strings in the source, so you need to edit it as UTF-8 text — modern IDE shouldn't mess it up. You also need to compile it with -gnatW8, if you are using GNAT. If you are not, I don't know if your Ada compiler will handle it correctly. Study your compiler's manual, and let me know in comments.

The output looks like this on my terminal:

Type categories

Judging from the corrections, once they called them classes, but the current Ada Reference Manual (for Ada 2012) uses the word categories. Anyway, here the categories which can be arranged hierarchically.

all types
- elementary
  - scalar
    - discrete
  - enumeration
    - character
    - boolean
    - other enumeration
  - integer
    - signed integer
    - modular integer
    - real
  - floating point
  - fixed point
    - ordinary fixed point
    - decimal fixed point
  - access
    - access to object
    - access to subprogram
- composite
  - untagged
    - array
  - string
  - other array
    - record
    - task
    - protecte
  - tagged (including interfaces)
    - nonlimited tagged record
    - limited tagged record
    - synchronized tagged
  - tagged task
  - tagged protected

Learning Ada 3: exploring types

Type or subtype, that's the question

Predefined types and subtypes

Seen “building blocks”

Source

Type categories