머클트리
등장 배경:
- 현재 비트코인 블록체인의 전체 크기는 약 160GB를 차지하고 있다. 비트코인의 사용량이 증가할수록 블록체인의 크기는 더욱 더 커질 것이다. 이는 블록체인이 거래내역을 저장하는 장부이기 때문이다. 효율적인 자료 저장을 위한 특별한 자료구조가 필요하다.
- 위변조를 확인하는 기능을 효율적으로 만들 필요가 있다. 160GB를 차지하는 자료들을 일일이 비교하며 특정 트랜잭션(거래)이 위변조되었는지 확인하는 건 너무 비효율적이다. 특정 트랜잭션의 위변조 여부를 빠르고 효율적으로 조회할 수 있어야 한다.
사용되는 기술:
- SHA256(SecureHashAlgorithm): 어떠한 입력값이 들어와도 항상 고정된 크기(256bit)의 데이터를 반환하는 해시함수
- Binary Tree(이진 트리): 트랜잭션의 해시(거래내역)를 두 개씩 묶어 또다른 해시를 만들어내는 알고리즘이 사용된다.
작동 방식에 대한 간략한 설명:
- 아래 그림을 기준으로 설명을 진행한다.
가정: 비트코인 블록체인의 특정 블록(100번 블록)안에는 트랜잭션들(A ~ P)이 존재하고 있다.
실제 구현: 각 트랜잭션들은 CTransaction 클래스의 1차원 vector로 CBlock 내에 저장되어 있다.
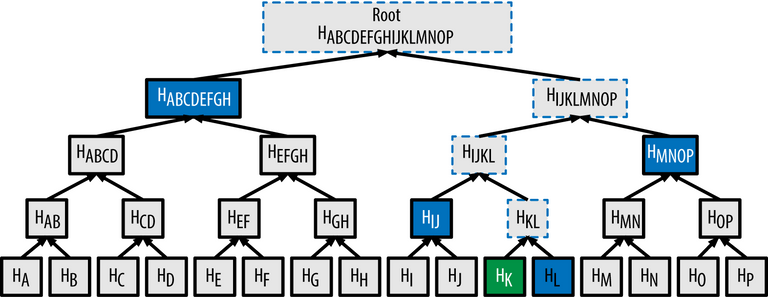
가지고 있는 트랜잭션 중 트랜잭션 K(위 그림에서 녹색으로 표시)의 위변조가 의심되어 위변조 여부를 조사하려 한다. 이때 필요한 정보는 파란색으로 칠해진 4개의 해시값(H_L, H_IJ, H_ABCDEFGH), 그리고 머클 루트다.
실제 구현: 각 트랜잭션들의 해시(uint 256: SHA256의 결과값은 unsigned 256bit)를 저장하기 위해 vector<uint256> vMerkleTree가 존재한다.트랜잭션 K의 위변조 여부를 조사하기 위해, K에 대한 해시값(녹색으로 표시)과 파란색으로 칠해진 4개의 해시값을 이용하면 머클 루트값(전체 거래내역 A~P에 대한 고유한 해시값)을 재구성할 수 있다. 두 개씩 차례로 이어붙인 후 그 값을 다시 해시하는 방식으로 루트값이 나올 때까지 반복한다. 전체 거래내역을 조회하는 것이 아닌, 단지 4개의 해시값만을 이용하여 위변조 여부를 검증할 수 있다는 건 매우 효율적이다.
실제 구현: 먼저 BuildMerkleTree( )메서드로 머클트리를 먼저 구성하고, 그 후 BuildMerkleBranch(매개변수: 위변조 검증을 원하는 트랜잭션의 해시) 메서드로 검증에 필요한 해시값들(위 그림 상에서 파란색으로 칠해진 값들)로 구성된 1차원 vector를 따로 제작한다. 이 vector를 머클 브랜치라 칭한다. 그 후 CheckMerkleBranch( ) 메서드로 머클 브랜치에 있는 해시값들, 그리고 위변조 검증을 원하는 트랜잭션을 가지고 검사를 진행한다.
비트코인코어 소스코드 리뷰 및 설명
main.h에 정의되어 있는 CBlock 클래스
class CBlock in main.h
// header: 흔히 말하는 블록 헤더의 정체다. 풀노드가 아닌 경량 클라이언트(light client)들은 블록 헤더만 저장하게 된다.
int nVersion;
uint256 hashPrevBlock;
uint256 hashMerkleRoot; // BuildMerkleTree()로 생성되는 머클루트
unsigned int nTime;
unsigned int nBits;
unsigned int nNonce;
// network and disk
vector<CTransaction> vtx; // 트랜잭션들을 저장할 때는 CTransaction 클래스의 벡터로 저장
// A block contains multiple transactions, held in vector<CTransaction> vtx.
// memory only
mutable vector\<uint256> vMerkleTree;
머클 트리의 생성(1)
- 머클 트리는 결국 1차원 벡터에 트랜잭션들에 대한 해시값을 채우고 2개씩 짝지어서 해시한 값을 삽입하는 방법을 사용한다. 고로 벡터의 마지막 원소는 항상 머클루트가 된다. 결국 이진트리(BinaryTree)를 1차원 벡터를 사용하여 구현한 것이다.
CBlock::BuildMerkleTree( )
uint256 BuildMerkleTree() const
{
vMerkleTree.clear();
// 각 트랜잭션들의 해시값을 따로 저장하여 vMerkleTree 생성
foreach(const CTransaction& tx, vtx)
vMerkleTree.push_back(tx.GetHash());
int j = 0;
for (int nSize = vtx.size(); nSize > 1; nSize = (nSize + 1) / 2)
{
for (int i = 0; i < nSize; i += 2)
{
// 만약 트랜잭션이 짝수개가 아니라면, 마지막 트랜잭션의 해시는 자기 자신과 해시하게 된다.
int i2 = min(i+1, nSize-1);
// 트랜잭션의 해시를 2개씩 묶어서 다시 머클트리에 삽입한다.
vMerkleTree.push_back(Hash(BEGIN(vMerkleTree[j+i]), END(vMerkleTree[j+i]),
BEGIN(vMerkleTree[j+i2]), END(vMerkleTree[j+i2])));
}
j += nSize; // j는 각 트리레벨에 맞춰 삽입해야할 첫번째 위치를 가리킨다.
}
return (vMerkleTree.empty() ? 0 : vMerkleTree.back());
}
머클트리의 생성(2)
- 머클트리의 생성(1)에서 설명한 소스코드를 활용하여 7개의 트랜잭션으로 1차원 vector를 구현한다면 아래와 같은 그림이 된다.
- 표기법 설명: H(tx[0]): 0번 트랜잭션(1번째 트랜잭션)에 대한 해시값 | H(66): 6번 트랜잭션(7번째 트랜잭션)에 대한 해시와 6번 트랜잭션에 대한 해시를 이어붙인 값을 다시 해시한 값; 앞서 말했듯 2개씩 묶어서 새로운 해시를 생성해야 하는데 7개의 트랜잭션이므로 홀수개다. 따라서 6번 트랜잭션(7번째 트랜잭션)은 자기 자신과 해시하는 방식으로 구현한다.

- 이렇게 2개씩 해시하고 벡터에 삽입하는 과정을 반복하면 벡터의 마지막에는 머클 루트가 자리잡게 된다.
머클트리의 증명(1)
- 특정 트랜잭션의 위변조 여부를 검사하기 위해서 모든 트랜잭션들을 검증할 필요는 없다. 필요한 트랜잭션 해시들만 선별한다.
// nIndex로 위변조 여부를 검사할 특정 트랜잭션을 선택하고 머클 트리내의 트랜잭션 해시값과 연관된
// 트랜잭션의 해시들만 따로 추출하여 MerkleBranch를 생성한다.
vector\<uint256> GetMerkleBranch(int nIndex) const
{ // nIndex에 해당하는 트랜잭션 증명에 사용되는 노드들을 vMerkleBranch에 담는 작업을 진행
if (vMerkleTree.empty())
BuildMerkleTree();
vector\<uint256> vMerkleBranch;
int j = 0;
for (int nSize = vtx.size(); nSize > 1; nSize = (nSize + 1) / 2)
{
int i = min(nIndex^1, nSize-1); // nIndex^1의 값은 0 또는 1(반복)
vMerkleBranch.push_back(vMerkleTree[j+i]);
nIndex >>= 1;
j += nSize;
}
return vMerkleBranch;
}
머클트리의 증명(2)
- 해시할 때의 규칙은 짝수에 해당하는 인덱스를 가진 해시는 다음에 해시될 때 좌측에 위치해야 한다는 것이고 홀수에 해당하는 인덱스를 가진 해시는 우측에 위치해야 한다는 것이다.
즉 SHA256(짝수인덱스를 가진 트랜잭션 해시, 홀수인덱스를 가진 트랜잭션 해시) 이렇게 구성된다는 뜻이다. 해시될 때의 순서에 따라 결과값은 완전 달라지기 때문에 순서 규칙을 지켜주는 것은 중요하다.
static uint256 CheckMerkleBranch(uint256 hash, const vector\<uint256>& vMerkleBranch, int nIndex)
{
if (nIndex == -1)
return 0;
foreach(const uint256& otherside, vMerkleBranch)
{ // 해시되는 순서를 지켜주기 위해 아래의 두 경우를 구분하여 처리
if (nIndex & 1) // 트랜잭션의 인덱스가 홀수일 경우
hash = Hash(BEGIN(otherside), END(otherside), BEGIN(hash), END(hash));
else // 트랜잭션의 인덱스가 짝수일 경우
hash = Hash(BEGIN(hash), END(hash), BEGIN(otherside), END(otherside));
nIndex >>= 1; // 해시되는 순서를 맞춰준다.
}
return hash; // it should be merkleRoot
}
머클트리의 증명(3)
- 머클트리의 증명(1), (2)를 도식화하면 아래와 같다.
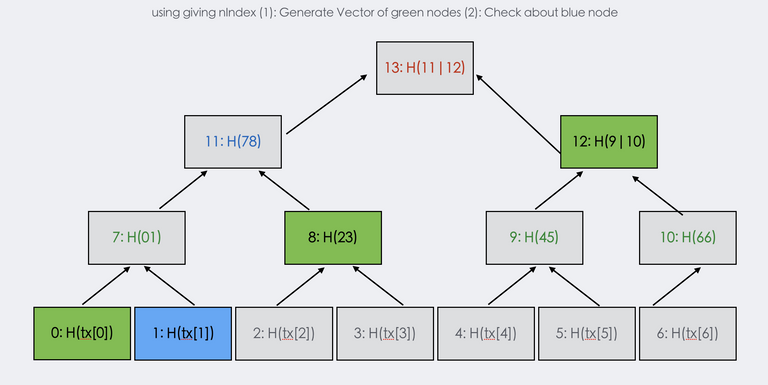
- 파란색에 해당하는 트랜잭션의 위변조 여부를 검사할 때 필요한 해시값은 초록색에 해당하는 해시값들이고, 그 해시값들을 이용하여 연산을 진행했을 때 머클루트값이 도출된다.
- 기존에 저장하고 있던 머클루트와 다른 값이 나왔다면, 트랜잭션에 위변조가 발생한 것이라고 판단할 수 있다.
마치며
- 간단한 개념이라도 이를 실수 없이 체계적으로 구현하는 건 어렵다는 걸 느꼈다. 직접 구현하기 위해 상당히 공을 들인 흔적이 비트코인 코어 소스에 그대로 담겨있는 걸 알 수 있다.
- 코드 중간중간 \가 붙은 파트가 있을 수 있는데, 이는 스티밋 블로그에 코드를 삽입할 때 꺽쇄 '<', '>'를 사용했을 때 업로드가 되지 않는 문제점때문에 취한 조치입니다. 그러니 읽을 때 헷갈려하지 않게 주의 바랍니다. 혹시 꺽쇄를 경고 없이 사용할 수 있는 방법을 아시는 분께서는 지식 나눠주시면 감사하겠습니다 :)
좋은 글 감사합니다.
도움이 되었다니 다행입니다 :)
Congratulations @dlgusdn616! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP