BITCOIN - what is inside

Everyone knows that Bitcoin is based on a complex cryptography algorithm. One such algorithm is SHA256.

Attempts to sort out this many led to failure. The block diagram of the algorithm SHA256 is distributed on the Internet.

This block scheme is correct, but it is not understandable to many, because the main drawback is that it is not indicated on it
where inputs are entered that need to be hashed. Everyone usually thinks that the data comes in
registers A, B, C, D, E, F, G, H. But this is not so. The input data comes byte-byte to the input W, and then only the first 16 of 64 cycles
a hash algorithm.

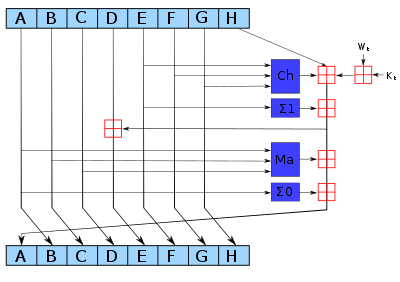
I bring to your attention my interpretation of the SHA256 hashing algorithm.

Before starting the hash calculation, the original message (M) must be supplemented with as many bits as possible so that the length of the message (L) is a multiple of 512.
To do this, 1 is added at the end of the message, then the number of zeros (n) is added to satisfy the equation: L + 1 + n = 448mod512.
The last 64 bits write the number of bits of the original message.
If the original message is more than 512 bits it is divided into (N) 512 bit blocks.
Each 512 bit is programmed into 16 blocks of 32 bits.

Original message (M) abc
a b c
01100001 01100010 01100011 ASCII

conversion message (m) abc

0110 0001 0110 0010 0110 0011 1000 0000 * W(0)=61626380

0000 0000 0000 0000 0000 0000 0000 0000 * W(1)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(2)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 *W(3)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(4)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(5)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(6)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(7)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(8)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(9)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(10)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 *W(11)=00000000

0000 0000 0000 0000 0000 0000 0000 0000 * W(12)=00000000

                              448bit #

0000 0000 0000 0000 0000 0000 0000 0000 * W(13)=00000000

#64bit
0000 0000 0000 0000 0000 0000 0000 0000 * W(14)=00000000

                     L massage(abc) 24 bit

0000 0000 0000 0000 0000 0000 0001 1000 * W(15)=00000018

In SHA256 there is an array of constants K (i).
Before starting the main hashing cycle, the array is assigned constants.

k[0..63] =
428A2F98, 71374491, B5C0FBCF, E9B5DBA5, 3956C25B, 59F111F1, 923F82A4, AB1C5ED5,
D807AA98, 12835B01, 243185BE, 550C7DC3, 72BE5D74, 80DEB1FE, 9BDC06A7, C19BF174,
E49B69C1, EFBE4786, 0FC19DC6, 240CA1CC, 2DE92C6F, 4A7484AA, 5CB0A9DC, 76F988DA,
983E5152, A831C66D, B00327C8, BF597FC7, C6E00BF3, D5A79147, 06CA6351, 14292967,
27B70A85, 2E1B2138, 4D2C6DFC, 53380D13, 650A7354, 766A0ABB, 81C2C92E, 92722C85,
A2BFE8A1, A81A664B, C24B8B70, C76C51A3, D192E819, D6990624, F40E3585, 106AA070,
19A4C116, 1E376C08, 2748774C, 34B0BCB5, 391C0CB3, 4ED8AA4A, 5B9CCA4F, 682E6FF3,
748F82EE, 78A5636F, 84C87814, 8CC70208, 90BEFFFA, A4506CEB, BEF9A3F7, C67178F2

Also, for calculations, the array h (i).
Before starting the main hashing cycle, the array is assigned constants.

h[0...7] =

h0 = 6A09E667
h1 = BB67AE85
h2 = 3C6EF372
h3 = A54FF53A
h4 = 510E527F
h5 = 9B05688C
h6 = 1F83D9AB
h7 = 5BE0CD19

Algorithm for computing the hash:

For i=1 to N / N is the number of 512 bit blocks in the converted message

      We prepare an array of additional messages W (i)

      The array W (0 ... 15) consists of 32 bit data taken from the transformed message (m)

      W(0)=61626380
      W(1)=00000000
      W(2)=00000000
      W(3)=00000000
      W(4)=00000000
      W(5)=00000000
      W(6)=00000000
      W(7)=00000000
      W(8)=00000000
      W(9)=00000000
      W(10)=00000000
      W(11)=00000000
      W(12)=00000000
      W(13)=00000000
      W(14)=00000000
      W(15)=00000018


      The array W (16 ... 63) must be generated according to the following algorithm

For i=16 to 63

    s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)
    s1 := (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10)
    w[i] := w[i-16] + s0 + w[i-7] + s1


   Initialization of auxiliary variables:

a = h0
b = h1
c = h2
d = h3
e = h4
f = h5
g = h6
h = h7

       Main Cycle:

For i=0 to 63

    E0 := (a rotr 2) xor (a rotr 13) xor (a rotr 22)
    Ma := (a and b) xor (a and c) xor (b and c)
    t2 := E0 + Ma
    E1 := (e rotr 6) xor (e rotr 11) xor (e rotr 25)
    Ch := (e and f) xor ((not e) and g)
    t1 := h + E1 + Ch + k[i] + w[i]

    h := g
    g := f
    f := e
    e := d + t1
    d := c
    c := b
    b := a
    a := t1 + t2

Add the obtained values to the previously computed result: 

h0 = h0 + a                                                       Example of the real end of the hash algorithm for the abc message:
h1 = h1 + b                                                       
h2 = h2 + c                                                       h0 = 6a09e667 + 506e3085 = ba7816bf
h3 = h3 + d                                                       h1 = bb67ae85 + d39a2165 = 8f01cfea
h4 = h4 + e                                                       h2 = 3c6ef372 + 04d24d6c = 414140de
h5 = h5 + f                                                       h3 = a54ff53a + b85e2ce9 = 5dae2223
h6 = h6 + g                                                       h4 = 510e527f + 5ef50f24 = b00361a3 
h7 = h7 + h                                                       h5 = 9b05688c + fb121210 = 96177a9c
                                                                  h6 = 1f83d9ab + 948d25b6 = b410ff61
                                                                  h7 = 5be0cd19 + 961f4894 = f20015ad
hash = h0  h1  h2  h3  h4  h5  h6  h7                             

                                                           hash(abc) = ba7816bf8f01cfea414140de5dae2223b00361a396177a9cb410ff61f20015ad

If the original message is greater than 512 bits (N> 0), the algorithm is repeated again, only the input data is taken from the following
block (512 bits) of the original message.

The article used the logical functions and, xor, shr (logical right shift), rotr (cyclic right shift).

    and   xor

0 0 -- 0 ----- 0
0 1 -- 0 ----- 1
1 0 -- 0 ----- 1
1 1 -- 1 ----- 1

I hope this article helped you understand the crypto algorithm SHA256