(image source: media.coindesk.com/uploads/2014/10/Bitcoin-security-630x334.jpg)

This post mainly follows the original Bitcoin whitepaper by Satoshi Nakamoto and explains the mathematics behind it in further detail.

Let's break the blockchain!

It's always a good idea in understanding the security of a system, to try to think about a way to destroy it! When you come to the conclusion that all such attempts are doomed to fail (which is what we are going to show), you can assume that the system is quite safe.

So let's pretend we are an attacker that wants to break a blockchain and fool the system, for example the Bitcoin network. What options do we have?

Every Bitcoin transaction contains a digital signature of the sender who signs it using his private key. It is very easy to validate that this signature comes in fact from the owner of the public key corresponding to private key and therefore from the owner of that Bitcoin address, yet it is extremely difficult to create such a signature without access to the private key. As an attacker, we would have no better option than just trying out random private keys until we find one that works. Since a private key is a 256-bit number, we would have to try on average 2^255 (I will not try to blow your mind with some weird comparisons on how big this number is, just know that it's big enough) keys until we find one that fits, which is a task, no entity, whether carbon- or silicon-based can ever complete in the lifetime of this universe.

So faking Bitcoin transactions won't work, how about faking Bitcoin blocks? As an attacker, we could set up our own Bitcoin node and feed the network with our own blocks. A block is only considered valid if the sha256-hash of the entire block begins with a certain amount of zeros. The object of the Bitcoin nodes is to find a "nonce", which is just a 32-bit number that sits in the header of every block, so that the hash of the entire block begins with a certain number of zeros. While it is unlikely for an individual to ever mine a block on it's own, even a small mining company with only 1% of the hashing power can expect to mine blocks on a regular basis.

So here's what we could do: We first broadcasts a transaction to a recipient in exchange for any kind of value (for example fiat currency). As soon as the transaction is included in a block, we try to feed the network with our own different version of the block, which does not include our own transaction. That way we hope to fool the recipient and get the money back. Let's say the transaction is included in block #n. The recipient waits for k confirmations before he accepts it, so now we are at block #(n+k).

The key feature about the blockchain is, that every block depends on the one that came before it (hence it's called a chain), so even if we managed to create an alternative version of block #n where our own transaction isn't included (or replaced by some other transaction), our version of the truth would not be accepted by the network because trust always lies within the longest chain of blocks. By altering even the slightest detail in a block, we completely change the resulting hash. Since every block always contains the hash of the previous block in its header, none of the following blocks would be valid any more and we would have to recompute all blocks #n until #(n+k) all on our own and outpace the main chain. Already this seems like a quite difficult task. Let's calculate the probability of such an attack being successful.

Let's say we, as an attacker, have a hashing rate of q, while the entire network has a combined hashing rate of p. So our proportion of the hashrate is given by

While the recipient is waiting for his k confirmations, we can already work on our altered version of block #n and the blocks after it in secret. Let X be the number of blocks that we managed to mine during that time. Since we are working with the proportion q/p of the hashing rate, X has the expected value of

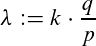
But what exactly is the probability for the different values of m, for example, what is P(X=0),P(X=1),... Luckily, there is a formula for that. This kind of statistical problem is described by the Poisson distribution and it comes with a formula:

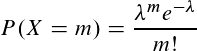
If we worked out less than k blocks, we are still (k-m) blocks behind the original chain. In that case, the probability of us ever outpacing the rest of the network is given by:

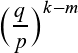
If we have already mined more than k blocks, we can just broadcast them to the network one by one and the probability of success is 1. For the final probability, we just multiply the probability of mining m blocks by the probability that we can still catch up from that point. If we now sum across all possible values of m, we get our end result

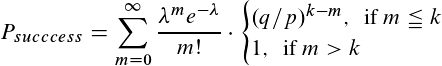
We can rearrange this formula to get a more easily computable result:

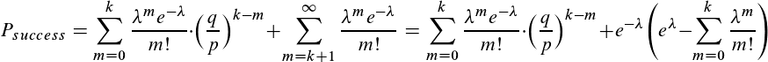
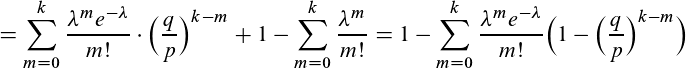
We can now plug in different values for k (the number of confirmations the recipients decides to wait for) and q/p (the proportion of the hashrate we control) and see what the probability for success is. Let's say for example, we control 10% of the hashrate, which for Bitcoin, would be quite a lot, and the recipient waits just for 1 extra confirmation. Even then, our chances of success are only 20,46%. Adding an extra confirmation lowers it to just 5.01%. If the recipient waits for 5 confirmation, our chances of success shrink to just 0,09%.

For any hashrate percentage lower than 10%, the chances of success become even lower. With more and more confirmations, the task becomes exponentially more difficult.

Even if some individual could acquire enough CPU power that such an attack would be possible, if the motives are of financial kind, he would be better of just playing by the rules and mine blocks for the reward.

The blockchain truly is secure as hell!

Sort:

Trending

[-]

mwhch (25) 7 years ago

Really good explanation of this topic.
For a visual description of the above mentioned method to ensure the blockchain can't be manipulated, this page can help: http://blockchain.mit.edu/blockchain/
Upon manipulating a block, the hash changes and thus all the blockchain entries after the manipulated block is different