Recursive program
Soon, we learned to write the equations and find out the value of recursive function in these two types of recursion trees. Now let's see how a computer program can be done by doing the same thing. Look at the C code below.
[code]
#include <stdio.h>
int F(int n) {
if (n == 0 ) return 0; /* this is equation (5) /
else if (n ==1 ) return 1; / this is equation (6) /
else return F(n-1) + F(n-2); / this is equation (7) */
}
int main(){
int input = 4; /* we want to compute 4th fibonacci number /
int output = F(input); / for input n, function F computes n’th fibonacci number /
printf (“the %dth Fibonacci number is %d\n”,input, output); /prints the output/
return 0; /terminate the program successfully*/
}
[/code]
If the input of function F is not 0 or 1 then the function is called for (n-1) and (n-2). When their value comes back, the output calculation is returned to their sum. The function reduces the value of its input when calling itself, so once the value of this input is 0 or 1, and the program returns to the line from number 5 or 6 without having to call it again.
If you want, you can test this program with the values of input in the main function.
However, if this recursive program is seen first, then the matter of calling itself to itself is not yet fully clear. Do not be afraid, we understand how this kind of program works very slowly now. And I will do it with some interesting examples. The first example is about the pylondrum.
Palindrom
There are interesting words or phrases in Bengal such as 'Ramakantakamara', 'Nayan', 'Fifth Dancer after Kirtan Manch', but they are the same from the opposite side. It is also in English, such as "Madam, I am Adam". They say the Palindrom. But during programming, we define the palladium, in such a way, if a string is reversed, it remains unchanged, that is, the palindrom. For example, "dcabacd", "nayan", "dad" is a pallidrum.
So we can think of some algorithms to check if there is no string palindrum. One is to create a copy of the string, reverse the copy. Then compare them with the original string and see if they are the same. Or if you do not want to copy, it is also checked with a loop. If the length of the string and the string is n.
[code language = "cpp"]
int pal (char * s) {
int b, e, n;
n = strlen (s);
b = 0;
e = n-1;
while (e> b) {
if (s [b]! = s [e]) return 0;
b ++;
e-;
}
return 1;
}
[/ code]
The functions b and e proceed according to the beginning and the end, and in the middle of any of the steps, the strings declare that the strings are not palindromes (returns 0). If there is no return from this loop, that means the string is palindrom. Then there is 1 return.
It is difficult to understand that the problem is not difficult. That is why we will write a recursive palm algorithm first to see how the recursive program works. That means, there are a few more interesting problems to wait for.
For that we can think of a function that gives two strings between the string and the string, returns the middle of the index, whether it is palindrome or not. Let us name the function rec_pal
If you type in C, you will see its signature.
[code language = "cpp"]
int rec_pal (char * s, int b, int e);
[/ code]
Where, s is the string's pointer. b is the starting index of the place you want to check. And e is the last index. If the function calls rec_pal (s, 0, n-1) where n is the length of the string, then the whole string is known to be palindrom.
Now we think that we want to check whether the palindrom is in the middle of the string s from e to the index. For him, we will first see s [b] and s [e] not equal. If not equal, then we can say that the string is not palindrom. And if it is equal, then the middle part is to check whether they are palindrome or not. In this work we can use the rec_pal function. That means,
[code language = "cpp"]
if (s [b]! = s [e]) return 0;
return rec_pal (s, b + 1, e-1);
[/ code]
This is being done in these two lines. First of all, starting and ending, ie, the position of b and e position is equal to two. If uneven we will return 0 directly. If they are equal, then from the right angle of b to the left of e to the left part of e, the string must be checked. For him the call will be rec_pal. Remember, we still do not know how rec_pal works. But if you want to do it, you can work just like the previous two steps. That means, the middle part will also look at the beginning and the end characters, and then again use rec_pal for the middle part. Thus, increasing b increases and decreases when one passes away, then it should be understood that the string is Palindrom. That means we can write the full function to the function as follows.
[code language = "cpp"]
int rec_pal (char * s, int b, int e) {
if (b> e) return 1;
if (s [b]! = s [e]) return 0;
return rec_pal (s, b + 1, e-1);
}
[/ code]
The function will be called from the main program for any input string.
[code language = "cpp"]
int main () {
int n, result;
char s [] = "nayan";
n = strlen (s);
result = rec_pal (s, 0, n-1);
printf ("% d \ n", result);
}
[/ code]
Now we will try to understand step by step how the rec_pal function for this input is s = "nayan"
Here the length of the string is n = 4 so call from main function rec_pal (s, 0, 3);
The program with this input will then be entered in the rec_pal function.
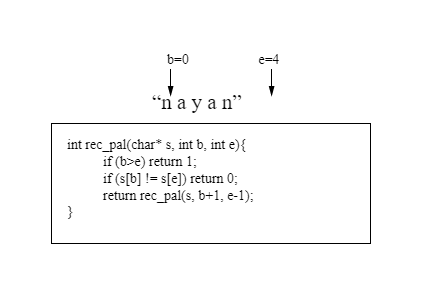
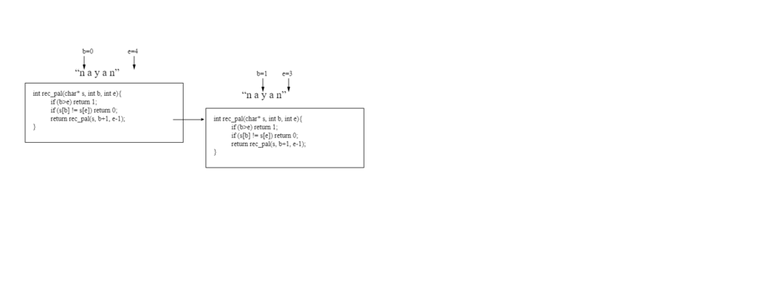
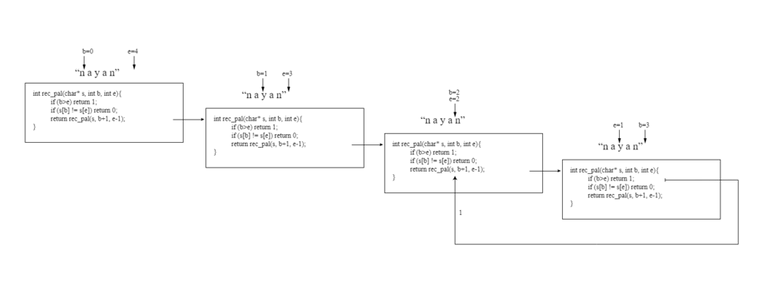
In Figure 2 (a), rec_pal in a box and its inputs are displayed. In this case, the input string is being indexed, both "nayan" and b and e starting and ending respectively. If the condition of the second line of the box is false then there will be nothing. Now we will see that from b to e index, the first and the last character of the string is the same. Seeing it in the third line If the condition of the third line is false, here s [b] and s [e] are equal. Now we have to see, whether the e-1 part from b + 1 is palindrom. For that, come to the fourth line, calling the rec_pal function again with s, b + 1 and e-1 input. Here the function is calling itself itself, so call it recursive call.
The computer uses such a call with its call stack. But for the sake of understanding, we will think, if a recursive call is made, then a copy of that function is created first. And with the changed inputs, the new copy starts running. This whole thing is meant to be in Fig. 2 (b). Where the right-hand box is the new copy of the function. A new box has been called from the line of the left box, from there an arrow arrives in the new box. And the new box inputs are shown above the box. Although the names of the new boxer variables are the same, since they are in new memory spaces, their values will be equal to the new inputs. That is why the value of b is in the left box 0 and the value of b is 1 in the right box b, but since they are different boxes variables, they may have their own values in their box. Now the third line of the box will be checked again, whether the new s [b] and s [e] are equal. They are equal in the right box. So again the middle part will be recursive call the same way. It is shown in Figure 2 (c).
Thus, this third box will call the function again for the fourth time (Fig. 2 (d)).
But now that the whole string is palindrome, it is checked. As a result, b will cross e and the first condition of this box will be true and 1 will return. Through an arrow we mean that. Please note that if the string is not palindrom, then if the condition is true in any previous step, it would return 0.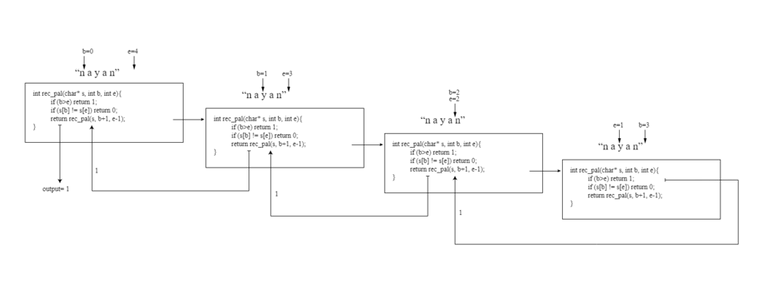
Verify yourself
Show how the rec_pal function works for "nabin" strings, as shown in Figure 2 (a) to 2 (e).
The sport with recursion
String print
Suppose we want to print every character of a string. There are thousands of ways to do this. For example, if the string is tahl only
[code language = "cpp"]
printf ("% s", s);
[/ code]
If you type the whole string will be printed.
If you want to print each character of the string in one of the loops one by one.
[code language = "cpp"]
int i;
char s [] = "abcde"
for (i = 0; s [i]! = '\ 0'; i ++) {
printf ("% c", s [i]);
}
[/ code]
But if Borong starts to loop, we can print the entire string with the help of our newly learned recursion. With the code below,
[code language = "cpp"]
void rec_print (char * s) {
if (s [0] == '\ 0') return; / * When the string ends, go back to nothing else * /
printf ("% c", s [0]); / * Print the string's first character * /
rec_print (s + 1); / * Then the rest of the print to print the Input
Call yourself recursive as * /
}
#include <stdio.h>
int main () {
int i;
char s [] = "abcde";
rec_print (s);
printf ("\ n");
return 0;
}
[/ code]
Here function rec_print (char * s) prints a string recursively. In the last line of the function, it is calling itself another copy of s + 1 input. We know that if s is the first character of a string's pointer. Then s + 1 is the second character of that string pointer. At the end of the string, there is always a last-pointing NULL character or '\ 0'. So in the first line of the function we see whether or not we reached the end of the string.
Verify yourself
By reciting the rec_print function, a function called rec_print2 can be written, where the last two lines have been drawn up. This means that the first character is printed after recursive call. Just like that
[code language = "cpp"]
void rec_print2 (char * s) {
if (s [0] == '\ 0') return;
rec_print2 (s + 1);
printf ("% c", s [0]);
}
[/ code]
In this previous program, use rec_print2 to see what the prints are. What is the change in output? Why?
Print an integer array element with n elements with recursive function.
Gassagu
We all know how to find two positive integers. One has to divide it and divide it into another. If there is no remaining, then you can get it. And if left, then the previous divisor will take a new divide and divide the previous one into the new divisor. This process continues until the end is 0. In this way, the sequence of time is 0. And then that's exactly the introduction of the introduction of the numerator of the numerator. This is the eclidian algorithm to extract the gassagoo.
The algorithm can be written in the form of a program,
[code language = "cpp"]
void gcd (int a, int b) {
int r;
while (1) {
r = b% a;
if (r == 0) return a;
else {
b = a;
a = r;
}
}
}
#include <stdio.h>
int main () {
int a = 12;
int b = 18;
int result;
result = gcd (a, b);
printf ("the gcd of% d and% d is:% d", the result);
}
[/ code]
But in the loop of the gcd function, we have done the same thing by replacing divisive bits according to each collection. So if you want to get rid of the Gassagoo recursion also,
[code language = "cpp"]
int rec_gcd (int a, int b) {
int r;
r = b% a;
if (r == 0) return a;
else return rec_gcd (r, a);
}
#include <stdio.h>
int main () {
int a = 12;
int b = 18;
int result;
result = rec_gcd (a, b);
printf ("the gcd of% d and% d is:% d \ n", a, b, result);
}
}
[/ code]
The rec_gcd function can be written in a line using the C operator's operator.
[code language = "cpp"]
int rec_gcd2 (int a, int b) {
return (b% a == 0? a: rec_gcd2 (b% a, a);
}
[/ code]
In other words, if b is a == 0 gsagu a nil, then recursively call rec_gcd2 will be replaced with the difference of the divisor.
Paramutations or Range
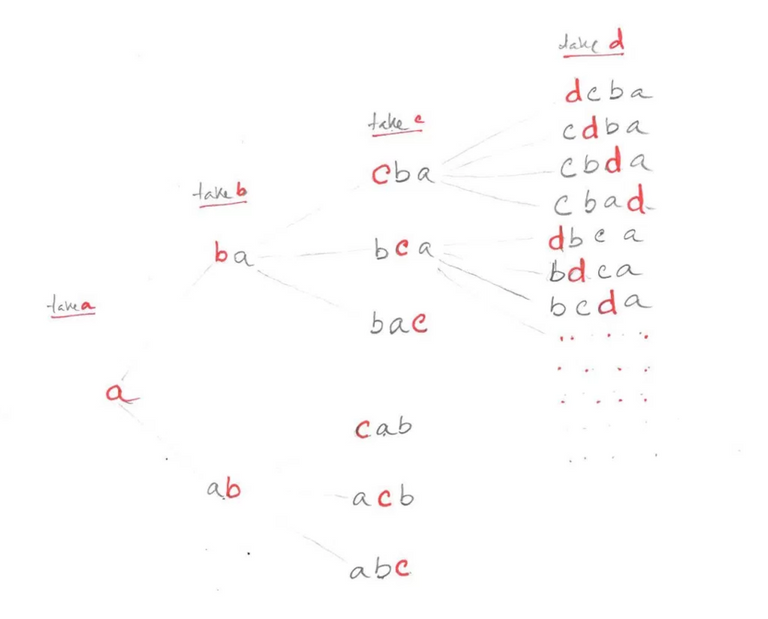
How many different things can be arranged in a row? We know the answer. Factorial n ways. We also learned the value extracting the value of factorial n (1) in the verification question. Now if you have to say n = 5 with the English character, to list all the possible formats, then write the total fact (5) = 120 strings. Without doing this work, writing a program is best. To understand what the program will be like, we have given the cursor only 4 a, b, c, d.
Now write the first one. After that, we can create two types of strings after b and a.
A) ba
B) ab
Now, for a few reasons, c can be placed in three places (before, sometimes, later). Thus, three lengths of the pie are 3 string
- cba
- bca
- bac
With that, b) No. String ab and in three places we get c,
- cab
- acb
- abc
Now if someone gives another character d, then there will be possible 4 types of these 6 types of String. And this way we get 6 \ times 4 = 24 strings.
The matter can be seen as the picture below,
Notice that we do not have a new one in each step of the 3 (a) figure, then we put them in all the possible straps of the current string and create a new string. This work is similar in every step. So it can be written with the help of a recursive function. That's why we will use C ++ now
[code language = "cpp"]
using namespace std;
string s = "abcd";
void perm (int take, string per) {
if (take == s.size ()) {
cout << per << endl;
return;
}
for (int i = 0; i <= per.size (); i ++) {
string str = per;
str.insert (i, 1, s [take]);
perm (take + 1, str);
}
}
int main () {
perm (0, "");
return 0;
}
[/ code]
The perm function comes in the input as a string per and a new character. Here the variables are meant to be the new character s [take].
As soon as it gets in hand, the perm function, first seeing every character in the string string has already taken all the characters, then print the string and return it. This is the function base case.
And if it does not, then create a new string by adding a new character to the front of the string, in every center and at the end. And the new string is again given as input of the perm function, along with the new character that has to take, take the index of take + 1 Thus, the function enters its next level.
The characters that have to take the permutation are in the above Global String. And at the beginning, main () is called perm (0, ""). Because at the very beginning we have a loose string, and we have to take the 0th character of s.
Random object formatting
In the previous section we have seen how to find all the different permutations or formatting of different objects. Now let's see if all things are not different, then what happens if some objects are the same. For example, if all three of these characters are asked to remove the permutations. Then it will be
baa
aba
aab
These three Where, the permutation of abc is possible 6. That means we need to change our function in such inputs. The modified function will be seen in the program with rep_perm.
[code language = "cpp"]
using namespace std;
string s = "aabbcc";
int c = 0;
void rep_perm (int take, string per) {
if (take == s.size ()) {
cout << per << endl; c ++;
return;
}
for (int i = 0; i <= per.size (); i ++) {
string str = per;
str.insert (i, 1, s [take]);
rep_perm (take + 1, str);
if (str [i + 1] == s [take]) break;
}
}
int main () {
rep_perm (0, "");
cout << "number of permutations:" << c << endl;
return 0;
}
[/ code]
How is this rep_perm working?
Let's say the characters are given as an input, b, b, c.
So at the beginning I get a strings
a
After that b will be able to sit before and after b
A) ba
B) ab
After that, take another b, and then put it a. At the beginning of the string. As a result,
- bba
But only after rec_perm's
if (str [i + 1] == s [take]) break;
These conditions will come true, that is, we will see that the new placement character matches exactly the previous character. So do not stop again. Because, if we put b in front of ba, or at the same time b b So it is enough to stop sitting once.
After that, b) start with the string and then start b b, then get it,
- bab
- abb
After that, that break again; The statement will be executed, so with the first three characters we get 3 strings.
Now we get every one of the string from 1 to 3 and we get it in the same manner as the figure -3 (a).
cbba
bcba
bbca
bbac
cbab
bcab
bacb
...
...
This is the total (4!) / (2!) = 12 strings.
Verify yourself
Complete the picture 3 (a). And use the rep_perm function for this input "abbcc" to draw an image like 3 (a).

I was summoned by @knowledgeup. I have done their bidding and now I will vanish...
A portion of the proceeds from your bid was used in support of youarehope and tarc.
Abuse Policy
Rules
How to use Sneaky Ninja
How it works
Victim of grumpycat?