
Las ecuaciones lineales en R3 tienen la forma ax + by + cz= k; donde a, b, c, y k son números reales tales que los coeficientes a, b y c son las variables o incógnitas; y k es una constante.
La solución de una ecuación lineal en R3 es un punto de coordenadas (x, y, z) en el espacio tridimensional.
Para obtener la solución de una ecuación lineal en R3 se presentan tres casos:
Supongamos que a ≠ 0
En este caso, despejando x podemos escribir la ecuación así:
x = (k – by – cz)/a
De tal forma que si asignamos valores a y y a z, obtendremos un valor respectivo para x.
Ejemplo: Consideremos la siguiente ecuación lineal en R3:
4x + 9y – 3z= 1
Despejemos x:
x = (1 – 9y + 3z)/4
Por ejemplo, si y=3 y z=4; entonces:
x= (1 -9x3 + 3x4)/4= ( 1 – 27 + 12)/4= (-14)/4= -7= -3,5
Por ello, una solución para nuestra ecuación es:
La triada (-3.5, 3, 4).
Esto es: 0x + 0 y + 0z = k
En este caso, la ecuación no tiene solución.
Esto es: 0x + 0y + 0z = 0
En este caso cualquier tirada (x,y,z) es solución para la ecuación.

Un sistema de ecuaciones lineales con tres ecuaciones y tres variables tiene la forma:
a 11x + a12y + a 13z= k1
a21x+ a22y + a23z= k2
a31x+ a32y + a33z= k3
Donde los aij y ki, son números reales e i y j son números naturales tales que 1≤ i ≤3.
y 1≤ j ≤3.

Un sistema de ecuaciones lineales puede ser inconsistente cuando no tiene solución y consistente cuando tiene una solución única o más de una solución.
Consideremos el siguiente sistema:
a 11x + a12y + a 13z= k1
a21x+ a22y + a23z= k2
a31x+ a32y + a33z= k3
Para resolverlo usaremos el siguiente procedimiento:
Para cada i>1, Li= -ai1L1 + a11Li
Esto es:
L2= -a21L1 + a11L2
L3= -a31L1 + a11L3
Veamos un ejemplo:
Resolver el siguiente sistema:
L1: 2x+ y -3z =5
L2: 3x - 2y +2z = 5
L3: 5x - 3y - z =16
Entonces a L2 la vamos a sustituir por la resultante de la siguiente operación:
L2= -3 L1 + 2L2
Esto es:
-3( 2x + y -3z =5)
+2(3x - 2y +2z = 5)
-6x -3y +9z =-15
6x - 4y +4z =10
Resultando L2 : -7y +13z =-5
Ahora trabajamos con L3
L3= -5L1 +2L3
Esto es:
-5 (2x + y -3z = 5)
2(5x - 3y - z = 16)
-10x -5y +15z =-25
10x -6y -2z = 32
-11y + 13z = 7
Haciendo las sustituciones en el sistema inicial, nos queda:
L1: 2x+ y -3z =5
L2: -7y +13z =-5
L3: -11y + 13z = 7
Vemos que si hacemos la operación -3 L2 + L se anulan las y.
Esto es:
-( -7y +13z =-5)
-11y + 13z = 7
7y -13z =5
-11y + 13z = 7
Resultando -4y = 12, despejando z, resulta que y=-3
Para hallar el valor de z, sustituimos el valor de y en la ecuación L2: y +10z =-28, esto es:
z =(7 + 11y)/13
Sustituyendo y por su valor y haciendo las operaciones correspondientes, se tiene que z=[(7+ 11(-3)]/13=[7-33]/13=26/13=2
Luego z=2
El valor de x se obtiene sustituyendo los valores de y y z en la ecuación L1:
2x -3 -3 (2)=5
2x -3 -6 =5
2x -9 =5
2x=5+9
x= 14/2=7
Luego las coordenadas del punto (x,y,z) que satisface las tres ecuaciones del sistema es (7, -3, 2), el cual corresponde a su solución.

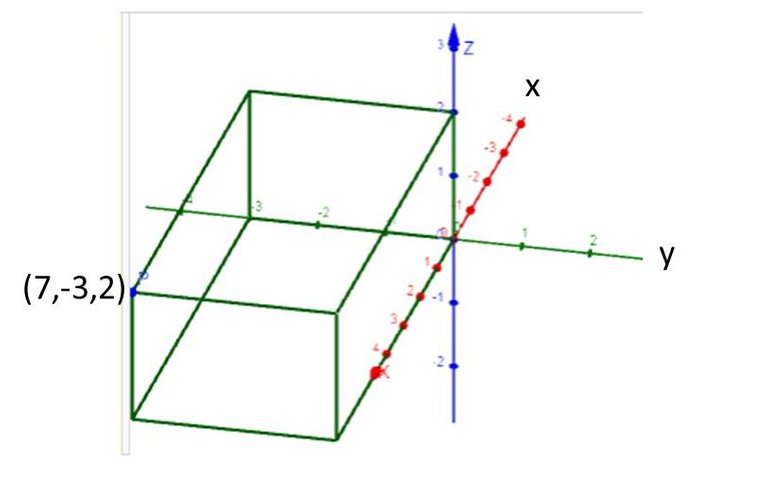
Gráfico elaborado por la autora con la ayuda de GeoGebra.

Créditos:
La imagen es recreada por la autora con apoyo de
Autor: George Hodan
Gracias por seguir mis sugerencias.
Nota: ¿Por qué no aplicar el método de Gauss-Jordan para solucionar el sistema?
Muy interesante tu sugerencia.
Saludos @lucioni. Mi respuesta a tu pregunta será mi próximo post. Abrazos.
Gracias @edu-venezuela.
Congratulations @analealsuarez! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard!
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
Felicitaciones profesora, excelente trabajo. Saludos.