El objetivo de este post es definir una función matemática a través de tres de sus representaciones como: conjunto, tabla de valores y en gráfica.
Fuente
Un par ordenado de coordenadas x e y se denota como (x,y) representa un punto en el plano R2
Donde x corresponde a la abscisa del punto, y la y corresponde a la ordenada.
Comencemos con los siguientes tres ejemplos:
A) Consideremos el siguiente conjunto de pares ordenados:
(x,y)={... (-2,-5), (-1, -1), (0,1), (1,3), (2,5)...}
Observemos que el conjunto de todos los puntos se encuentran vinculados por una regla que asigna a cada elemento x un elemento y, ésta está dada por y=2x+1; eso puede ser verificado ya que cada vez que multiplicamos por 2 a la x de cada punto o coordenada obtendremos el valor y correspondiente a ese punto, por lo cual cada par ordenado viene dado por el par general:
(x, y= 2x+1).
| x | y=2x+1 | (x,y) |
|---|---|---|
| -2 | y=2(-3)+1=-6+1=-5 | (-2,-5) |
| -1 | y=2(-1)+1=-2+1=-1 | (-1,-1) |
| 0 | y=2.0 + 1= 1 | (0,1) |
| 1 | y=2.1+1=2+1= 3 | (1,3) |
| 2 | y=2.2 +1= 5 | (2,5) |
Ubiquemos esos puntos sobre el Plano R2
Vemos que al unir los puntos la gráfica generada es una recta.
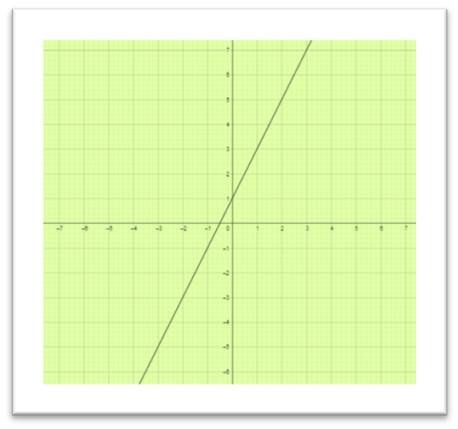
La gráfica corresponde a una recta.
B) Veamos ahora con este otro conjunto de pares ordenados:
(x,y)= {...(-2,4), ( -1,1), (-0.5, 0.25), (0,0), (0.5, 0.25), (1,1), (2,4)...}
Aquí vemos que a cada x le corresponde su cuadrado; por lo tanto, la regla que relaciona a cada coordenada x con una respectiva y es x2
Costruyamos la tabla de valores:
| x | y=x2 | (x,y) |
|---|---|---|
| -2 | y=(-2)2 | (-2,4) |
| -1 | y=(-1)2 | (-1,1) |
| -0.5 | y=(-0.5)2 | (-0.5, 0.25) |
| 0 | y=02 | (0,0) |
| 0.5 | y=0.52 | (0, 0.25) |
| 1 | y=12 | (1,1) |
| 2 | y=22 | (2,4) |
Ubiquemos los puntos sobre el plano, y construyamos la gráfica.
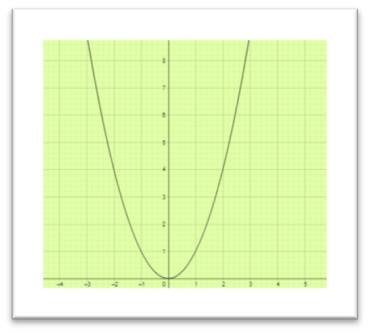
La gráfica obtenida corresponde a una parábola que abre hacia arriba.
C) Continuemos con este conjunto:
(x,y)={... (0,0), (1,-1), (1,1), (4, -2), (4,2), (9,-3), (9, -3), (16, -4), (16, 4)...}
La regla en este caso es y= +/- (√x)
Construyamos la tabla de valores:
| x | y= +/- (√x) | (x,y) |
|---|---|---|
| 0 | y= +/- (√0) | (0,0) |
| 1 | y= +/- (√1) | (1, -1) y (1,1) |
| 4 | y= +/- (√4) | (4,-2) y (4,-2) |
| 9 | y= +/- (√9) | (9,-3) y (9,3) |
| 16 | y= +/- (√16) | (16, -4) y (16, 4) |
Tracemos el gráfico en el plano R2
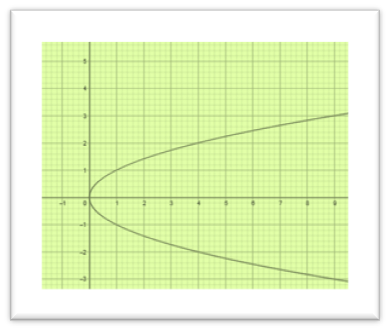
En este caso se trata de una parábola que abre hacia la derecha, observe que cada x es el cuadrado correspondientes a dos valores de la y.
Vamos ahora a usar un criterio de análisis en cada ejemplo planteado que nos permita
diferenciar ¿en cuál de las gráficas anteriores se identifica el hecho de que: a cada
valor de x le corresponde un único valor de y?
Comenzando por el ejemplo A, vemos que se cumple el criterio de análisis, a cada x le corresponde una única y; lo mismo sucede con el ejemplo B; pero el criterio falla en el ejemplo C, ya que para cada x no hay una única y; aquí vemos que el criterio se cumple solamente para 0 cuyo único valor y que le corresponde es 0, pero en cada uno de los demás valores de x existen dos valores para la y rompiéndose así el criterio de que cada x debe estar vinculada con una única y.
Los tres ejemplos corresponden a una relación definida por una regla de correspondencia, pero específicamente, las relaciones que cumplen con el criterio de análisis planteado anteriormente, reciben el nombre de función, las relaciones que no cumplen este criterio son consideradas simples relaciones más no funciones.
Entre los tres ejemplos planteados, el A y el B representan a una función, el C es una simple relación.
En el caso especial de las funciones, la regla puede ser denotada por: f, g, h, o, cualquier otra letra del alfabeto en minúscula. Por ello escribimos en el caso A, f(x)=2x+1; y en el caso B, g(x)=x2
; lo cual corresponde a la notación funcional donde la y es sustituida por f(x), g(x), ...
Hasta aquí tenemos definido el concepto de función en matemática, pero en la vida real también se aplica este concepto. Por ejemplo entre la relación madre e hijo no puede existir una función debido a que una madre puede tener varios hijos; pero en la relación hijo madre si hay una función, porque un hijo solo puede tener una única madre biológica.
Veo que quedó harto claro su objetivo didáctico. La felicito. ¡Es que la matemática es eso... un lenguaje que nace de la vida real y se dirige a ésta; ello a punta de movimientos descriptivos, probables y futuros! Todo en abreviaciones.
Gracias @alexandermoreno, aprecio su comentario.
Que bien trabajado tu post, felicitaciones @analealsuarez.