Este post tiene por objetivo ofrecer a la comunidad estudiantil de Steemit el desarrollo de un ejercicio matemático que sé que va a ser de interés para muchos.

Resolver la siguiente ecuación:
x3= 4x2-3x
Solución:
La ecuación planteada es un polinomio de tercer grado, por lo tanto, ha de tener máximo tres raíces o menos.
Antes de resolver quisiera dar algunos ejemplos previos para ilustrar la afirmación anterior:
Veamos:
Primer ejemplo para ilustrar que una ecuación de 3er. grado puede tener solo una raíz.
Consideremos la ecuación x3=0, para que esta expresión sea igual a 0, necesariamente la base de esa potencia tiene que ser 0; esto significa que x=0, lo cual corresponde a la solución de esa ecuación.
También se puede comprobar que x3+ x=0 tiene una sola solución real.
Segundo ejemplo para ilustrar que una ecuación de 3er. grado puede tener dos raíces solamente.
x3 - x2=0
Para resolver esta ecuación vamos a sacar factor común x2, y nos queda: x2 ( x-1)=0, de donde x2=0 si y únicamente si x=0, y, x-1=0 significa que x=1. Por lo tanto, esta ecuación polinómica de 3er. grado tiene solo dos soluciones: x=0 y x=1.
Comencemos ahora con el ejercicio propuesto
Existen diferentes maneras de resolver esta ecuación, entre ellas, la gráfica de la función es muy importante por cuanto permite visualizar las raíces; para elaborar la gráfica nos podemos auxiliar con una aplicación en línea llamada Symbolab; esta es la gráfica.
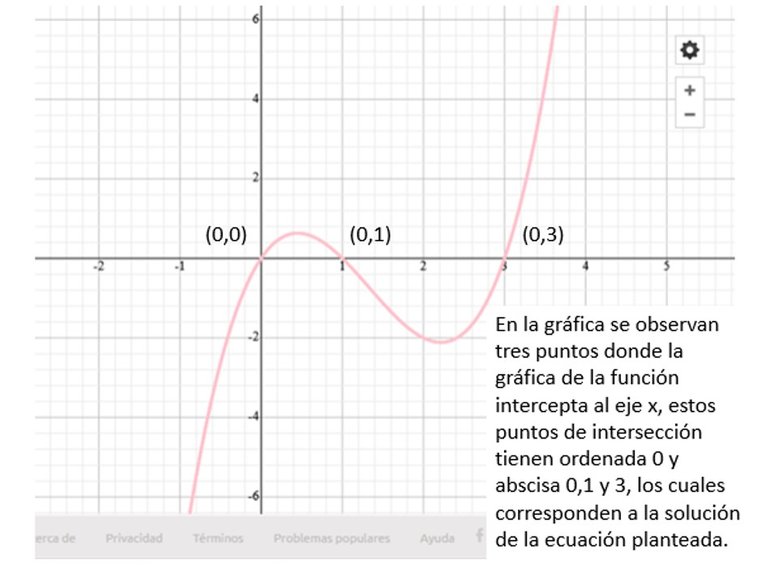
Con esta información vamos más seguros al momento del proceder algebraico para resolverla.
Veamos
Primero igualamos la ecuación a 0, así:
x3 - 4x2+3x=0
Luego sacamos factor común x, así:
x(x2 - 4x+3)=0
Aplicamos la siguiente propiedad de las operaciones con números reales:
Si a y b son dos números reales, y su producto es igual a 0; esto es, si a.b=0, entonces a=0 o b=0 (*)
Considerando a=x y b= x2 - 4x+3 entonces x=0 o x2 - 4x+3= 0
De aquí se obtiene la primera solución de la ecuación, x=0; para obtener el resto de las soluciones resolveremos la ecuación de segundo grado:
x2 - 4x+3= 0
Vamos a factorizar esta ecuación usando el siguiente criterio:
La factorización de x2 +(a+b)x+a.b= (x+a)(x+b) donde a y b son números reales:
De modo que para factorizar nuestra ecuación bajo el criterio anterior nos hace falta conseguir los números a y b cumplan lo siguiente:
a+b=-4 y a.b=3
Estos números son: a= -3 y b= -1, es decir que:
x2 +4x+3= (x-3)(x-1)
Igualando a 0 para obtener la raíz, nos queda:
(x-3)(x-1)=0
Aplicando de nuevo el criterio (*)
Nos resulta que:
(x-3)(x-1)=0 entonces x-3=0 y x-1=0
Despejando x obtendremos las dos raíces restantes:
x=3 y x=1
La solución es: x=0, x=3 y x=1
Te dejamos pendiente la siguiente ecuación: x4 - 9x2= -6x2
Referencias
Jorge Saenz (1993). Cálculo para Administración y Economía. Editorial Hipotenusa. Venezuela.