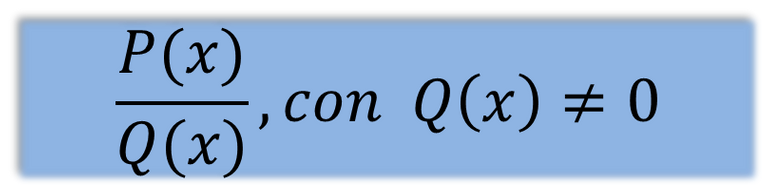
Una expresión racional en el contexto aritmético se refiere a una expresión
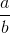donde a y b son números reales y 
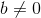, es decir b diferente de cero. Pero en el contexto algebraico, el numerador a puede ser sustituido por un polinomio P(x) y b por 
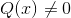( ¿Por qué?), donde x es una variable real en la cual P y Q están definidas; es decir, x está en el dominio de las funciones polinómicas P y Q.Consideremos el ejemplo siguiente :
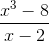, Vemos que P(x)=
y
Q(x)=
. La variable x debe estar tanto en el dominio de P(x) como en el de Q(x); como ambas son funciones polinomiales, entonces su dominio es el conjunto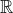 
de los números reales. Pero recuerde que P(x) debe ser diferente de cero, entonces debemos eluir los valores de x que hacen que el denominador se haga igual a cero; en este caso es 2, ya que Q(2)=2-2=0. Por ello los valores de la variable deben estar en el conjunto de los números reales diferentes de 2, es decir:
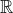-{2}.3=8, nos queda:
Es decir, nuestra función racional queda reducida a una función cuadrática.
Observe que hay posibilidad de simplificar esta función racional si factorizamos el numerador y luego simplificamos. Recuerde la fórmula para factorizar es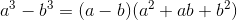 
. Luego, aplicando la fórmula para a=x y b=2, recuerde 2
.
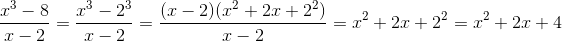Esto es 
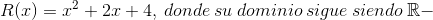{2}
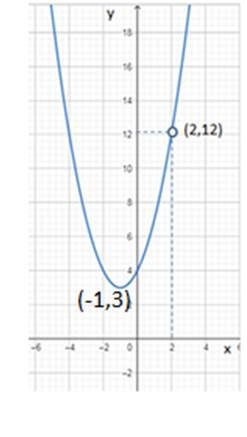
Veamos la gráfica de esta función racional
Créditos:
Las ecuaciones se realizaron con la ayuda del editor en linea de Ecuaciones LateX.
La gráfica se hizo con la ayuda de GeoGebra Clásico.
En este caso particular, la gráfica de la función racional nos resulta una parábola cuyo vertice se encuentra en el punto (-1,3) y que esta definida en todo número real x a excepción de x=2; consecuentemente, su imagen que es 12 no se encuentra en el recorrido de la función, el cual consiste en el intervalo que va desde [3, +
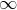) -{12}
El cociente de dos polinomios recibe el nombre de función racional y se denota por R(x), en este caso R(x)=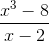. El dominio de la función racional consiste en todos los números reales a excepción de aquellos valores que hacen que el polinomio denominador Q(x) se haga igual a 0.
Buen trabajo @anmilet. Si tienes algún tiempo, te invito a ver mi post sobre la Energía. Saludos.