En este post se quiere establecer la vinculación existente entre la derivada de una función y su continuidad en un punto, para ello vamos a realizar, a través de un proceso de inducción, una serie de ejemplos donde trataremos de aclarar tal punto en plan de generalizar.
In this post we want to establish the link between the derivative of a function and its continuity at a point, for this we are going to perform, through a process of induction, a series of examples where we will try to clarify this point in order to generalize.
Para ello, se hace necesario comprender el significado de Diferenciabilidad de una función f, en tal sentido se debe acudir a la identificación de la derivada con la pendiente de la recta tangente al gráfico de f en un punto de su dominio, de manera que recomiendo leer este post que hice en alguna oportunidad sobre el tema en referencia Interpretación geométrica de la Derivada de una función en un punto.
For this, it is necessary to better understand the meaning of the Differentiability of a function f, then it is necessary to remember the relationship that exists between the derivative and the slope of the tangent line to the graph of f at any point.
To remember this relationship it is necessary to review the following post: Geometric Interpretation of the Derivative of a function at a point.
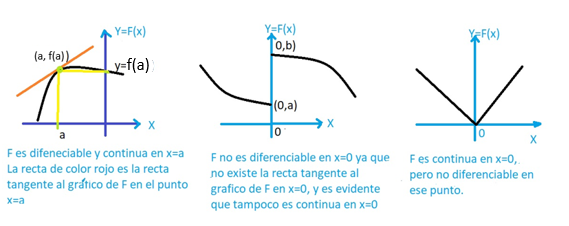
Y es que, vinculamos la diferenciabilidad de una función f en un punto x=a con la existencia de la recta tangente al gráfico de f en el punto x=a; si esa recta no existe, entonces decimos que f no es diferenciable en x=a.
And is that, we link the differentiability of a function f at a point x=a with the existence of the tangent line tangent to the graph of f at the point x=a; if that line does not exist, then we say that f is not differentiable at x=a.
Veamos a continuación:// Let's take a look at the following:
Definición
Se dice que una función f es diferenciable en un punto x=a si y solo las derivadas unilaterales existen en ese punto y si, además, son iguales.
Esto es:
Definition
A function f is said to be differentiable at a point x=a if and only the unilateral derivatives exist at that point and if, in addition, they are equal.
This is:
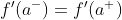.gif)
Ahora consideremos la siguiente función: //Now let us consider the following function:

Cuya gráfica es la siguiente: // The graph of which is as follows:
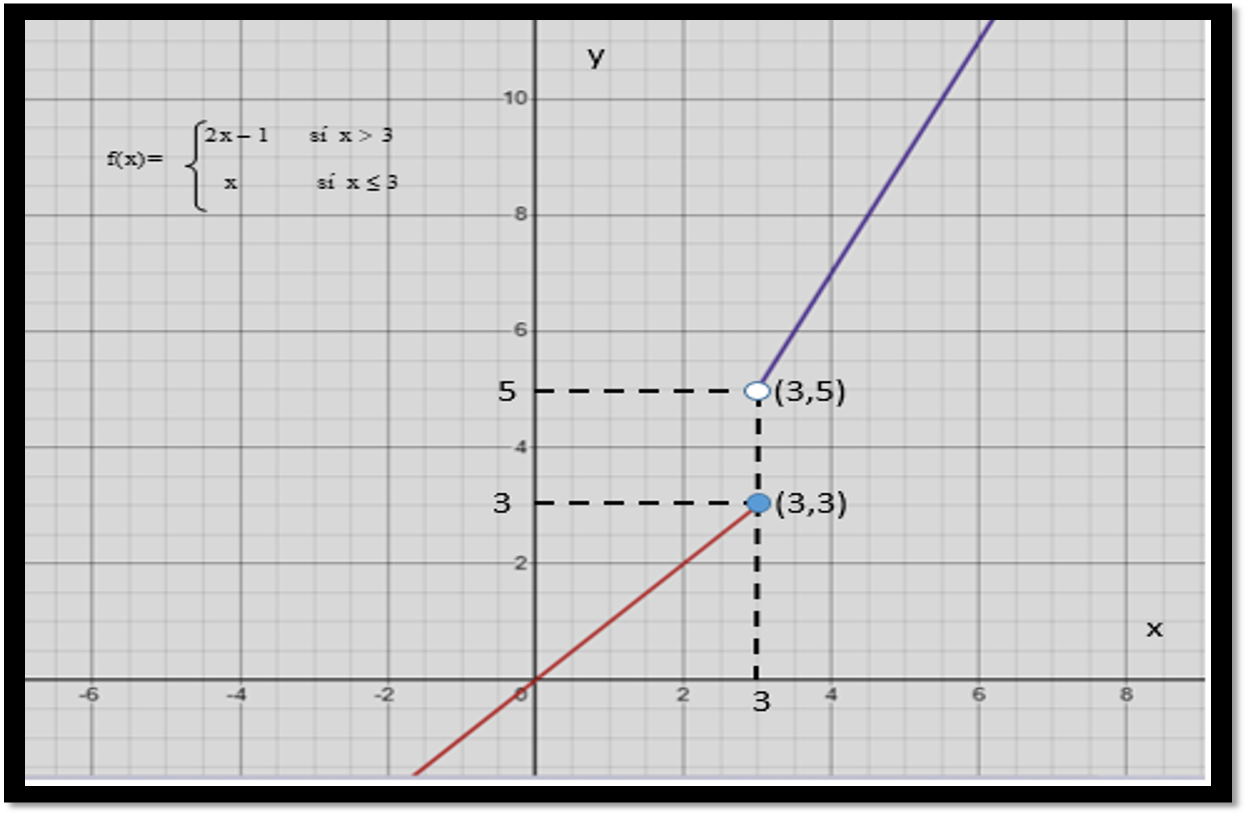
Vemos en la gráfica que f no es continua en x=3 // We see in the graph that f is not continuous at x=3
¿Cual es la derivada de esta función? // What is the derivative of this function?
Vemos en la gráfica, que es imposible trazar la la recta tangente a f en x=3, por lo tanto f no es diferenciable en x=3. // We see in the graph, that it is impossible to trace the tangent line to f at x=3, therefore f is not differentiable at x=3.
Esta función es seccionada, en tal sentido existe una derivada por la izquierda de 3 y una derivada por la derecha 3. // This function is sectioned, in this sense there is a derivative on the left of 3 and a derivative on the right 3.
Esto es lo siguiente:
La derivada de f por la izquierda de 3 se denota: 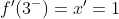.gif) y la derivada por la derecha es:
y la derivada por la derecha es: .gif)
Se ve claramente que las derivadas unilaterales existen pero no son iguales, consecuentemente f no es diferenciable en 3.
This is as follows:
The derivative of f on the left hand side of 3 is denoted:and the derivative on the right hand side is:
It is clear that the unilateral derivatives exist but are not equal, consequently f is not differentiable in 3.
Nota: // Note:
Esta función no es diferenciable pero tampoco es continua. // This function is not differentiable but it is not continuous either.
Estudiemos la función valor absoluto en el punto x=0 // Let's study the absolute value function at point x=0
La función valor absoluto se define así: // The absolute value function is defined as follows:
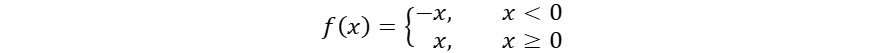
Le dejamos la gráfica al lector. // We leave the graph to the reader.
Vemos, de acuerdo a los criterios de continuidad vistos en este post CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO, que esta función es continua en x=0
We see, according to the continuity criteria seen in this post CONTINUITY OF A FUNCTION AT A POINT, that this function is continuous at x=0
Pero, de acuerdo a los criterios de diferenciabilidad, f no es diferenciable en x=0 ya que: // But, according to the differentiability criteria, f is not differentiable at x=0, since:
.gif)
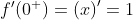.gif)
Como podrás observar, el hecho de que una función sea continua en un punto no nos garantiza que sea diferenciable en dicho punto.
As you can see, the fact that a function is continuous at a point does not guarantee that it is differentiable at that point.
Veamos lo contrario: // Let's look at the opposite:
Esto es: // This is:
Si una función f es diferenciable en un punto entonces nos preguntaríamos ¿es f es continua en ese punto? // If a function f is differentiable at a point then we would ask is f continuous at that point?
Para este caso consideremos la función f(x)= x3. // For this case consider the function f(x)= x3.
Recuerda que su gráfica es: // Remember that its graph is:
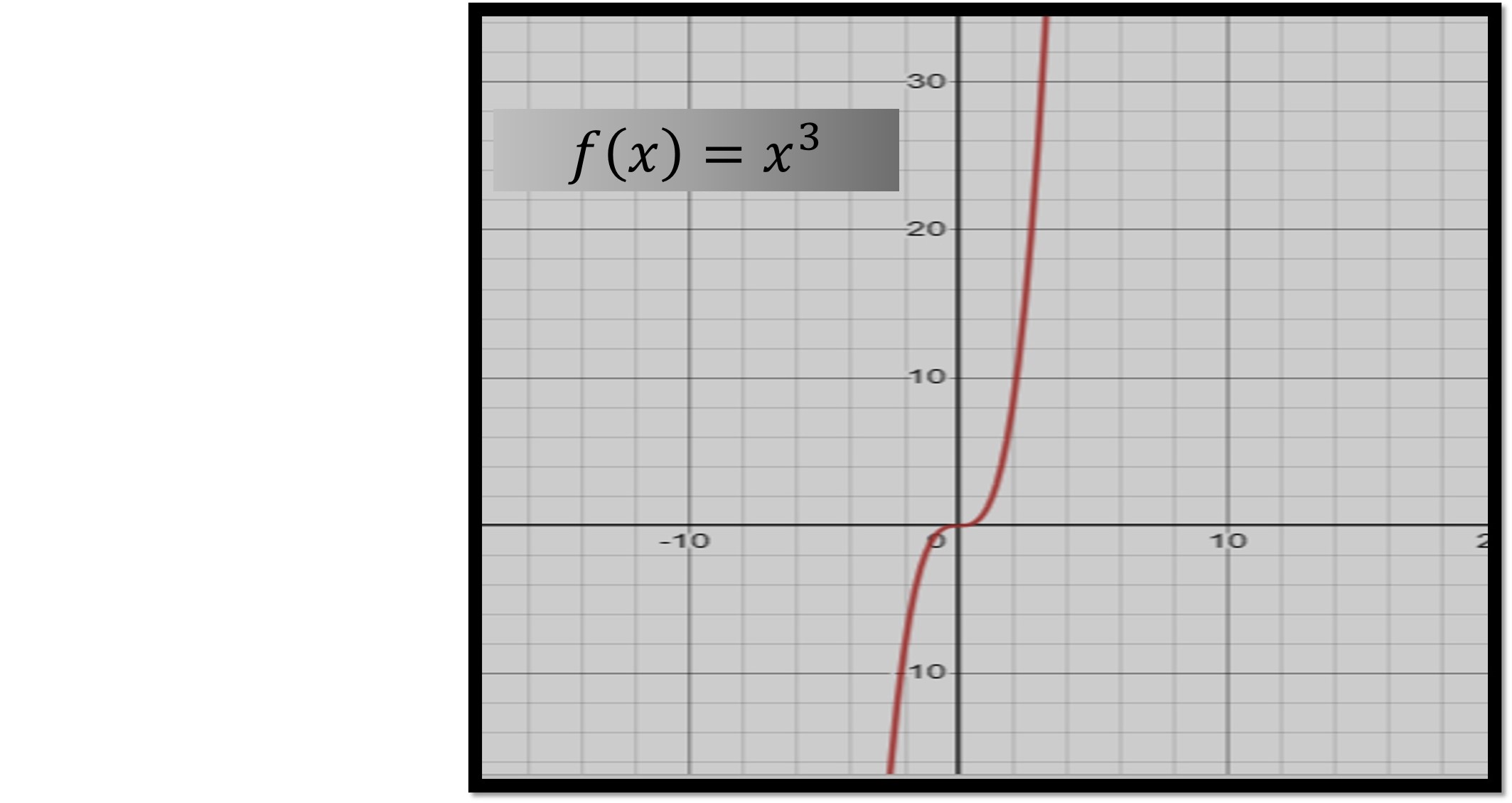
Si preguntamos: // If we ask:
¿Es diferenciable en cualquier punto de su dominio? // Is it differentiable at any point in your domain?
Responderemos que: // We will answer that:
Sí, es diferenciable para todo x de su dominio .//Yes, it is differentiable for all x in its domain .
.gif)
¿Es dicha función continua en cualquier punto de su dominio? //Is this function continuous at any point in its domain?
También lo es, f es continua en todo su dominio ya que es una función polinomica. // Also, f is continuous over its entire domain since it is a polynomial function.
Conclusiones: // Conclusions:
Con estos ejemplos podemos ilustrar lo siguiente:
- Con el primer ejemplo vimos una función no continua y no diferenciable en un punto.
- En el segundo ejemplo vimos una función continua pero no diferenciable en un punto.
- Con el tercer ejemplo nos conseguimos con una función diferenciable y continua.
Podemos generalizar esto diciendo que
Toda función diferenciable es continua, pero no toda función continua es diferenciable.
With these examples we can illustrate the following:
- With the first example we saw a function not continuous and not differentiable at a point.
- In the second example we saw a continuous function but not differentiable at a point.
- With the third example we got a differentiable and continuous function.
We can generalize this by saying that
Every differentiable function is continuous, but not every continuous function is differentiable.
Créditos: // Credits
El contenido es totalmente original de la autora.
Para las gráficas utilicé la calculadora gráfica Desmos, PawerPoint y Paint
Para las ecuaciones usé el Editor de Ecuaciones Latex.
For the graphs I used Desmos graphing calculator, PawerPoint and Paint.
For the equations I used Latex Equation Editor.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.