Comencemos este post con la siguiente cita:
“El gran libro de la naturaleza está escrito en lengua matemática, cuyos caracteres son los triángulos, los círculos y otras figuras geométricas”.
Galileo.
Año 1623.

Para el filósofo griego Platón (427-347 a. C.) las ciencias matemáticas son el fundamento de todo el saber humano, y en tal sentido le dio una gran importancia en la formación de filósofos de su época, de tal forma que creó una academia para formar filósofos dónde el eje transversal de la formación de estos fue la matemática.
Para él la matemática tiene como objetivo elevar el alma de las cosas sensibles a la verdad ideal inteligible, cognoscible por vía exclusivamente racional, es decir, por el pensamiento. Platón, consideraba la existencia de un mundo inteligible el cual llamó "el mundo de las ideas" donde se encuentra la matemática conformada por todos sus objetos ideales; afirmaba Platón que tales objetos matemáticos ideales tienen su correlato en la realidad sensible, por ejemplo una rueda en el mundo sensible tiene su correlato en el mundo de las ideas, ese correlato es un círculo. Señala Platón que tales objetos en el mundo sensible carecen de la perfección de sus correlatos en el mundo de las idealidades; es decir, tales correlatos no llegan a la perfección de los objetos ideales de la matemática, que le toca al pensamiento racional elevarlos, por lo tanto, todo objeto real o del pensamiento es el reflejo de un objeto matemático.
Tomando como fundamento estas ideas y considerando que históricamente la matemática ha sido herramienta fundamental de la ciencia para crear conocimiento, consideramos importante mencionar desde el punto de vista epistemológico la Teoría General de Sistemas (TGS); como una filosofía de la ciencia cuyos fundamentos no están muy lejos de las consideraciones de Platón.
Para la TGS, la matemática es una herramienta que la ciencia debe utilizar para organizar la totalidad, para la TGS la totalidad es la realidad sensible(ciencias naturales y sociales) y el pensamiento organizado en un todo como sistema conformado por subsistemas.
Lo anterior corresponde a una visión del mundo como un todo organizado a través de leyes que no vemos o isomorfismos matemáticos.
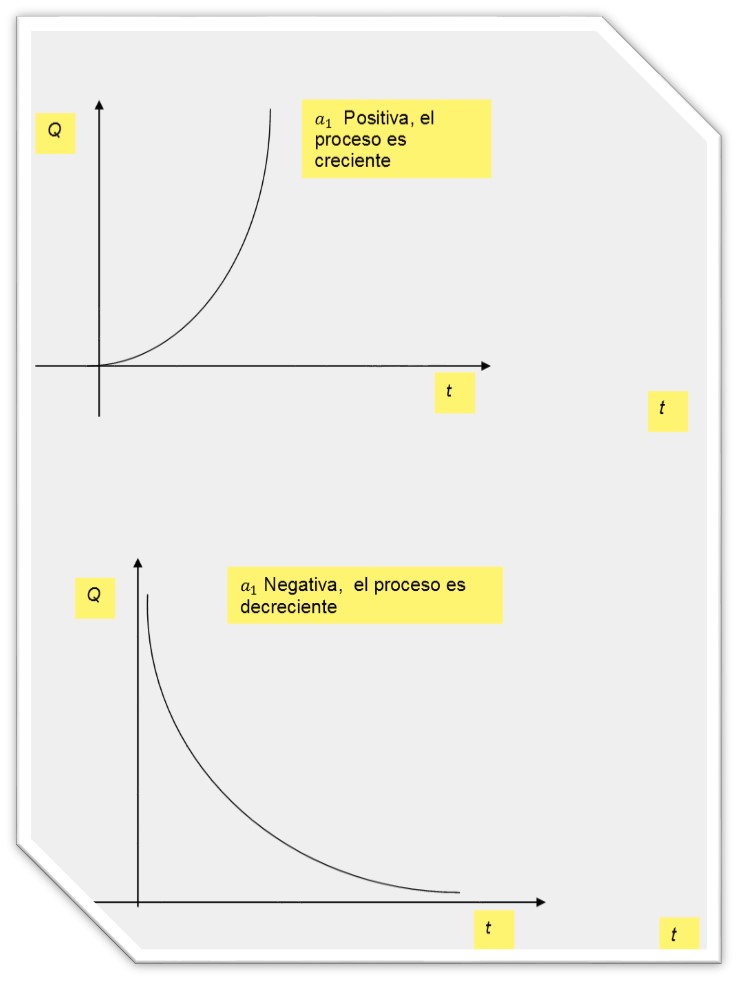
Es por ello existen modelos matemáticos que sirven para explicar fenómenos en diferentes contextos, tal es el caso de la ley exponencial:
Q=Q0 ea1 t
En esta ecuaciónla letra Q representa la magnitud que se quiere estudiar en el instante t > 0, Q0 es el valor inicial de la variable cuando el tiempo t =0 y a1 representa la tasa de crecimiento instantánea entre t=0 y t>0, y finalmente la constante e=2.718281828459…
Esta ley cuando a1 es positiva es usada en:
Matemáticas bajo el nombre de ley de crecimiento natural y es usada para el cálculo del aumento del capital por interés compuesto.
Biología se aplica para determinar el crecimiento individual de ciertas bacterias y animales.
Sociología para determinar la multiplicación sin restricción de poblaciones vegetales o animales.
Ciencias sociales se llama Ley de Malthus y representa el crecimiento ilimitado de una población cuya tasa de natalidad es superior a la mortalidad.
Cuando a1 negativo
Esta ley describe situaciones que disminuyen o decrecen, tal es el caso de la desintegración radiactiva, la descomposición de un compuesto químico por reacción molecular, el exterminio de bacterias por radiación o veneno, a la pérdida de sustancia corporal por hambre en un organismo multicelular y, al ritmo de existencia de una población en la cual la tasa de mortalidad superior a la de la natalidad.
Referencia
Bertalanffy, Ludwig v. Teoría General de Sistemas. Fondo de Cultura Económica. México, 1980https://es.wikipedia.org/wiki/Plat%C3%B3n
