Show Notes for: #Cicada3301 Liber Primus, 47th Problem of Euclid, Pythagoras Triangles, Music Encryption

Image Source: https://steemkr.com/cicada3301/@j1337/cicada-3301-tribute-and-searching-for-paths-in-2018-following-rabbit-holes-and-loose-ends

Show Notes:

Cicada 3301 Music Drops...

The Well:

Dust:

Cicada 3301 Art...

Layers upon layers:

Ana Couper art: ~~~ embed:1484419542944456705?s=20 twitter metadata:YW5hX2NvdXBlcnx8aHR0cHM6Ly90d2l0dGVyLmNvbS9hbmFfY291cGVyL3N0YXR1cy8xNDg0NDE5NTQyOTQ0NDU2NzA1fA== ~~~

Art 2:

Shout out to the New Cicada 3301 Liber Primus Solving Group on Discord ...

Solfa Cypher: ~~~ embed:1484542327918055429?s=20 twitter metadata:SW1wZXJhdG9yVHJ1dGh8fGh0dHBzOi8vdHdpdHRlci5jb20vSW1wZXJhdG9yVHJ1dGgvc3RhdHVzLzE0ODQ1NDIzMjc5MTgwNTU0Mjl8 ~~~

The 47th Problem of Euclid

[Unlike the Harpedonaptae, you have no way to establish true North and South...unless you use a compass. But a compass isn't necessary for this demonstration.
However, you WILL be able to create a perfect square...with only sticks and string, just as our ancestors did.
You will need 4 thin sticks which are strong enough to stick them into soft soil, 40 inches of string and a black magic marker. Actually, any length will work, but this size is very manageable.
The larger the foundation which the Mason wished to build, naturally, the longer his rope (string) would have to be.
Place your 1st stick flat on the ground so that its ends point north and south.

Next, take a string (it's much more unwieldy if you use rope) and tie knots in it, 3 inches apart. This will divide the string into 12 equal divisions.

Tie the 2 ends of the string together (this is your 12th knot) ...again ...remember that from knot-to-knot it must be 3 inches apart. The divisions between knots must be correct and equal or it will not work.

Your string's total length is 36". After you've tied the end-to-end knot, you may cut off the excess 4" of string.

If you have more than 4" of string left or less than 4" of string left, you need to re-measure the lengths between your knots.

Your string is now circular in shape and has 12 knots and 12 divisions between the knots. (see the Right Triangle, again, below)

Note: The Operative Masons of old, used rope, however, because much of the length of the rope is within the knot, if you use rope, you must use a longer piece, measure each division, tie your knot, and then measure your next 3 inch division before you cut the length of rope, instead of marking the entire rope while it is lying flat and then tying your knots.

Stab your 2nd stick in the ground near either end of your North/South stick and arrange a knot at the stick.

Stretch 3 divisions away from it in any direction (9 inches) and insert the 3rd stick in the ground, then...

Place the 4th stick so that it falls on the knot between the 4-part and the 5-part division (12 inches).

This forces the creation of a 3:4:5: right triangle. The angle between the 3 units and the 4 units is, of necessity, a square or right angle.
Now, move your 3rd and 4th sticks until they become a right angle (90 degrees) to your North/South stick.

Congratulations! You now have not only the ability to square your square, but to lay a geometrically correct cornerstone for your new foundation!]

"Theory"

In set theory, inversional equivalency is the concept that intervals, chords, and other sets of pitches are the same when inverted.[citation needed] It is similar to enharmonic equivalency, octave equivalency and even transpositional equivalency. Inversional equivalency is used little in tonal theory, though it is assumed that sets that can be inverted into each other are remotely in common. However, they are only assumed identical or nearly identical in musical set theory.

Sets are said to be inversionally symmetrical if they map onto themselves under inversion. The pitch that the sets must be inverted around is said to be the axis of symmetry (or center). An axis may either be at a specific pitch or halfway between two pitches (assuming that microtones are not used). For example, the set C–E♭–E–F♯–G–B♭ has an axis at F, and an axis, a tritone away, at B if the set is listed as F♯–G–B♭–C–E♭–E. As another example, the set C–E–F–F♯–G–B has an axis at the dyad F/F♯ and an axis at B/C if it is listed F♯–G–B–C–E–F.]

[...The "pitch axis" works in the context of the compound operation transpositional inversion, where transposition is carried out after inversion. However, unlike in set theory, the transposition may be a chromatic or diatonic transposition. Thus, if D-A-G (P5 up, M2 down) is inverted to D-G-A (P5 down, M2 up) the "pitch axis" is D. However, if it is inverted to C-F-G the pitch axis is G while if the pitch axis is A, the melody inverts to E-A-B.
The notation of octave position may determine how many lines and spaces appear to share the axis. The pitch axis of D-A-G and its inversion A-D-E either appear to be between C/B♮ or the single pitch F...]

https://en.m.wikipedia.org/wiki/Pythagorean_interval

[Frequency ratio of the 144 intervals in D-based Pythagorean tuning. Interval names are given in their shortened form. Pure intervals are shown in bold font. Wolf intervals are highlighted in red. Numbers larger than 999 are shown as powers of 2 or 3. Other versions of this table are provided here and here.]

https://commons.wikimedia.org/wiki/File:Interval_ratios_in_D-based_symmetric_Pythagorean_tuning_(powers_of_2_%26_3).PNG

[The first to mention the comma's proportion of 531441:524288 was Euclid, who takes as a basis the whole tone of Pythagorean tuning with the ratio of 9:8, the octave with the ratio of 2:1, and a number A = 262144. He concludes that raising this number by six whole tones yields a value G which is larger than that yielded by raising it by an octave (two times A). He gives G to be 531441....]

https://en.m.wikipedia.org/wiki/Pythagorean_comma

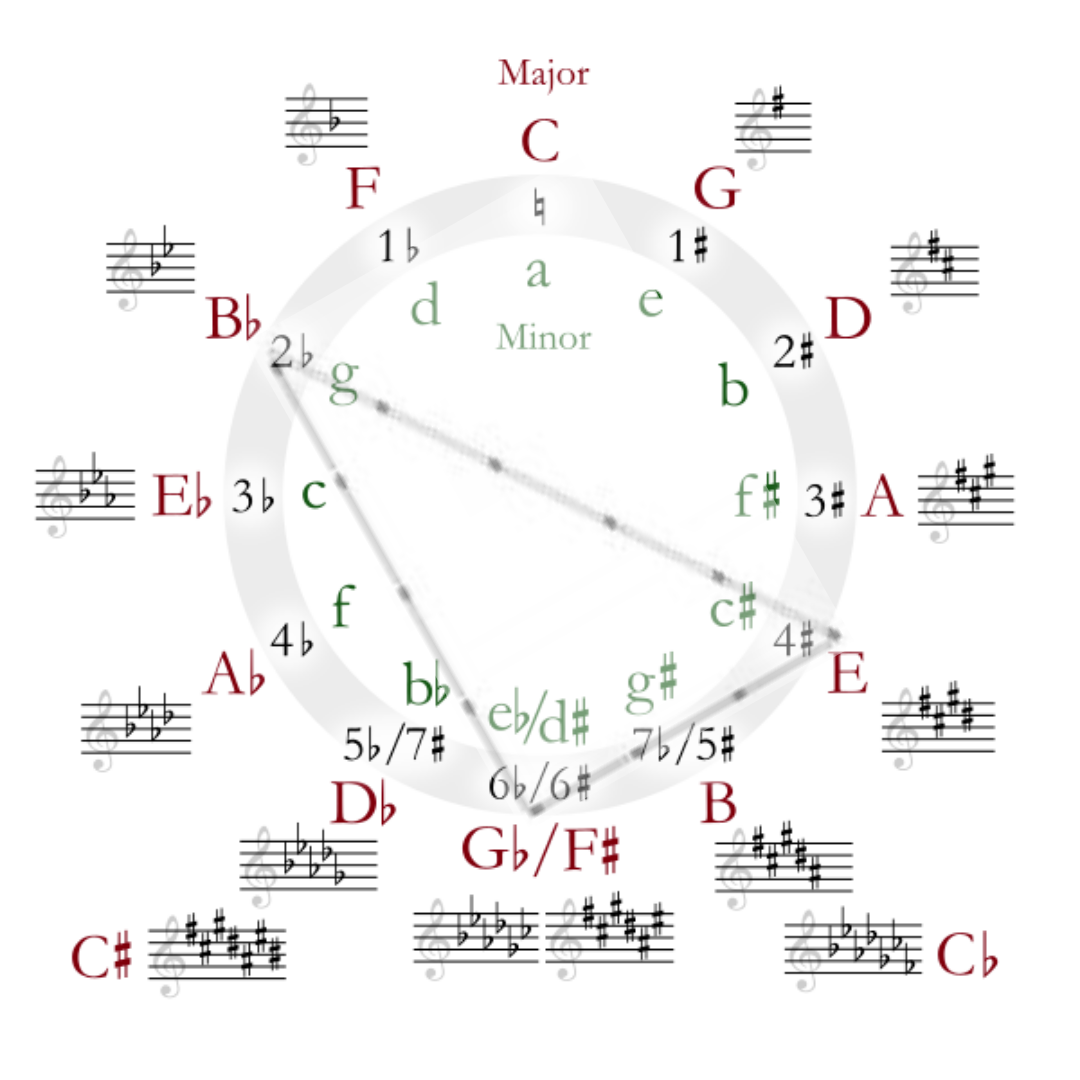
Pythagorean interval
In musical tuning theory, a Pythagorean interval is a musical interval with frequency ratio equal to a power of two divided by a power of three, or vice versa. For instance, the perfect fifth with ratio 3/2 (equivalent to 31/21) and the perfect fourth with ratio 4/3 (equivalent to 22/31) are Pythagorean intervals.
All the intervals between the n...

Pythagoran Tuning: https://commons.wikimedia.org/wiki/File:Interval_ratios_in_D-based_symmetric_Pythagorean_tuning_(powers_of_2_%26_3).PNG

A neume (/njuːm/; sometimes spelled neum)[1][2][3] is the basic element of Western and Eastern systems of musical notation prior to the invention of five-line staff notation.: https://en.m.wikipedia.org/wiki/Neume

Thanks to the Cicada 3301 solving group on discord for the above revelations! We have a great new team of solvers who are not about egos, they are about doing solid work. Cheers to those still on the path.