学习回归分析篇---之一元线性回归分析应用例

[shenzehe]

我们首先来研究一个实例。

一个活塞，底部为一个均匀地排布了网状小孔的漏筛，筒里装有粘性流体，流体在重力作用下，会从小孔漏出。 顶部有一个活塞，活塞上部可以加砝码。加载的砝码越重，流体流出越快。 这个装置用来测试粘性流体的流动性能，表征流体的加工性能。这种装置有标准，供测试塑料加工性能之用。

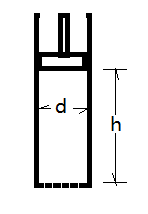
图 3.1 测试粘性流体的流动特性的装置

一次测试的数据样本如表 3.1 所示 (注：这里所有表格和图形都取自我自己写的工艺优化软件，OAO V1.0, 关于这个软件，我们以后介绍。)

表 3.1 测试数据样本（在回归分析程序中的显示形态）

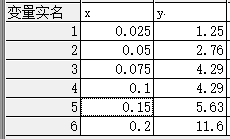
显然，随活塞顶部加砝码重量不同，底部流出的量不同。流体力学认为，流出量与顶部压力成正比，

y∝b₁x ------(3.1)

这六个试验点描绘在坐标系统上，如图 3.2 所示

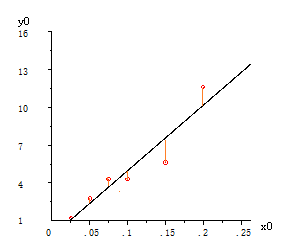
图 3.2 测试数据点绘（在回归分析程序中的显示形态）

试验数据并未整齐地表现出这种正比关系。试验总是有误差的，每个点都可能有误差。 假定每个试验的误差为e_i(i=1,2,...,6)。 实验误差是多少是未知的。实验误差的估计与试验范围的大小有关，试验范围越宽，误差估计越精确。 实验误差的估计还与试验样本的大小有关，试验点数越多（样本越大），误差估计越精确。 重复试验可以帮助更精确地估计误差，重复的次数越多，误差的估计越精确。详见有关教程。

我们如何估计在其他负重情况下的流出量呢？这就是回归分析的任务。根据式(3.1)表达的实验模型， 建立回归模型。

y=b₀+b₁x + e ------(3.2) 调用回归分析过程可以估计出回归方程中的参数 b₀ 和 b₁，得到预报方程 y=β₀+β₁x ------(3.3) 它就是 图 3.3 中的那条直线。

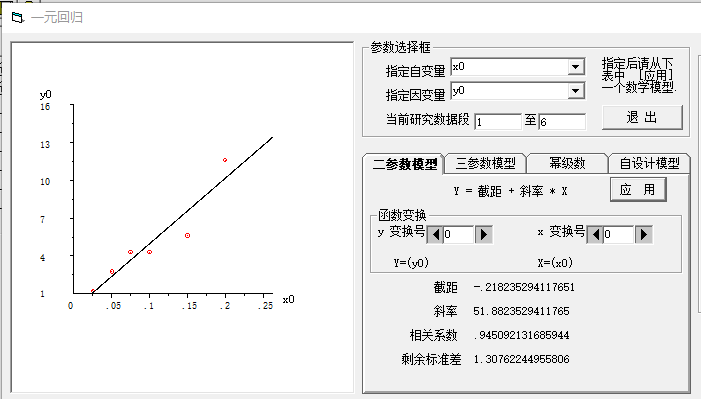
图 3.3 回归直线

关于回归分析的算法，我们后面介绍。首先研究上面这个例子的一些问题。

按照这个测试的实验模型，当顶部不加砝码时，活塞没有负荷， x=0 时, 应该有 y=0. 即，回归直线应该通过坐标原点。现实并非如此，如何解释？

即使 x=0, 被测试物质有自重。这个重量加在筒底，会使被测试物质漏出。只不过速度很慢就是了。 这个值是直线的截距。这个值应该大于 0，而回归方程中的截距小于 0，这就意味着实验误差。 我们来观察各个实验的误差估计，

图 3.4 误差描绘

回归直线与每个试验点的距离就是那个点的实验误差估计。某些点有正误差，另一些点有负误差。 代入回归方程会发现，正负误差相等。所以，回归直线一定通过 x,y 的中值点(x^-,y^-)。 如果能够断定，回归直线一定通过坐标原点，那么，坐标原点与(x^-,y^-) 就决定了这条直线。

回归直线是否恰当地表达了样本中的两个变量之间的关系？需要有一个衡量、检验的标准。 这个标准可以是两个变量的相关系数。回归分析图 3.3 中给出了本例的相关系数为 r=0.9451。 严格来说，单用相关系数来衡量是不够的。相关系数的大小依赖于样本的大小。统计需要有一个临界值。 大样本和小样本的统计效果不一样。统计学上用相关性置信水平 α 或置信概率 p(=1-α) 来衡量。 通常，如果置信概率大于或等于0.95，就说该判断在统计学意义上有0.95的可靠性。 如果置信概率大于或等于0.99，就说该判断在统计学意义上有0.99的可靠性。 于本例，

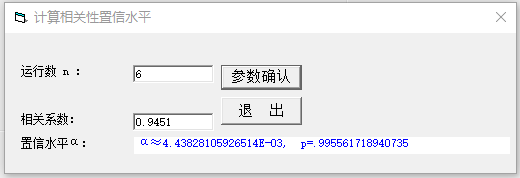
图 3.5 置信概率估计

置信概率大于 0.99。用线性模型拟合样本足够好。

有关回归分析的数学描述，我们下一节介绍。

参 考

1. 茆诗松,丁元,周纪芗,吕乃刚编著,《回归分析及其试验设计》,华东师范大学出版社,上海,1981
2. T.Hastie,R.Tibshirani,J.Friedman, The Elements of Statistical learning, Springer-Verlag,New York,2001
3. J.S.Milton, Jesse C.Arnold, Introduction To Probability and Statistics,(Third Edition ),1995