拜占庭将军问题
起源

拜占庭是东罗马帝国的首都,但是当时候拜占庭罗马帝国国土面积非常大,为了更好的防御,军队就被分成了很多小部分,而且间隔距离很远,将军们之间的消息只能靠差使来传递。而在战争的时候,一个军队的实力不足以抗衡敌人阵营,所以所有军队必需达成共识,能否战胜敌方。而在军队里面有可能存在叛徒和敌方间谍,影响 左右将军的决定,扰乱军队秩序。而有可能最终达成的结果并不代表大多数人的意见。所以在已知有反叛情况下,前提其他将军忠诚度不变的情况下,如何解决信任协议问题呢?这就是拜占庭问题。
PBFT
拜占庭将军问题其实就是一个协议问题,它是对现实世界的模型化。如果我们在信息传输过程,由于硬件错误、网络拥堵断开、或者遭到恶意攻击,计算机网络都可能出现不可预测的问题。而拜占庭协议就要如何处理在这些失效,并且还要满足问题的规范。下面给大家讲讲PBFT的算法。
拜占庭问题,一致性确保 主要分为:预准备、准备,确认。
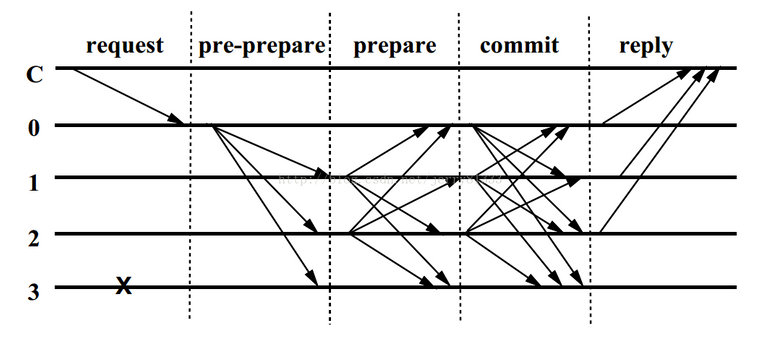
算法来源 来自于CSDN
其中C为发送请求端,0123为服务端,3为宕机的服务端,具体步骤如下:
- Request:请求端C发送请求到任意一节点,这里是0。
- Pre-Prepare:服务端0收到C的请求后进行广播,扩散至123。
- Prepare:123,收到后记录并再次广播,1->023,2->013,3因为宕机无法广播。
- Commit:0123节点在Prepare阶段,若收到超过一定数量的相同请求,则进入Commit阶段,进行commit请求。
- Reply:0123节点在Commit阶段,若收到超过一定数量的相同请求,则对C进行反馈。
根据上述流程,在 N ≥ 3F + 1 的情況下一致性是可能解決,N为总计算机数,F为有问题的计算机总数。
N=4,F=0
| 节点 | 得到数据 | 最终数据 |
|---|---|---|
| a | 1 1 1 1 | 1 |
| b | 1 1 1 1 | 1 |
| c | 1 1 1 1 | 1 |
| d | 1 1 1 1 | 1 |
N=4,F=1
| 节点 | 得到数据 | 最终数据 |
|---|---|---|
| a | 1 1 1 0 | 1 |
| b | 1 1 1 0 | 1 |
| c | 1 1 1 0 | 1 |
| d | 1 1 1 0 | 1 |
N=4, F=2
| 节点 | 得到数据 | 最终数据 |
|---|---|---|
| a | 0 1 1 1 | NA |
| b | 1 0 1 1 | NA |
| c | 1 0 1 1 | NA |
| d | 1 0 1 1 | NA |
我们可以从列表中看出拜占庭容错算法,能够容纳1/3的节点错误。它有效的解决了协议的统一性。