Chapter 2 Digital Signature
數碼簽名同紙張上既簽名一樣,目的係要簽紙果個人無得抵賴佢同意,發佈左一份文件。
例如我寫左份合約,「如果聽朝8點仲掛緊八號風球,我就切JJ」,仲起上面簽個名。
點知聽朝8點真係仲掛緊,你就可以拎住份合約黎,「拿上面你簽左名,無得抵懶啦,拎條J黎」
現實世界既簽名係有弱點:冒簽。
我可以反口話「尋日另一個人扮我簽名,我唔會認我賭過J架」
呢個時就口同鼻拗,又要搵筆跡專家鑑定,或者下次賭J既時候要簽指模先算數。
但係數碼簽名就唔同喇,除非竊漏左你既秘密,否則無人扮到你簽名。
個秘密係咩?係一條private key
顧名思義,private key係只有你可以知道,因為你唔想其他人冒認你既身份,用你條priavte key黎簽名。
同private key相對既另一條key叫做public key
public key就全世界都可以知道,係用黎比人判斷一個簽名係咪你簽既。
如果文件上面既簽名係用另一個人既private key整出黎,咁你用underpant's public key去驗証,就會失敗
如果文件上面有underpants's private key 製造出黎既簽名,你用underpant's public key黎驗証先會成功。
驗証成功左,咁我就無得賴啦。
用兩個function黎表達上面段字:
簽名=sign(underpant's private key, 文件)
簽名有效=verify(簽名, 文件, underpant's public key)
verify呢個function會return true or false, 視乎簽名/文件/public key三樣野夾唔夾。
例如
verify(sign(underpant's private key, 文件), 文件, underpant's public key) 會return true
verify(sign(腦魔's private key, 文件), 文件, underpant's public key) 會return false
verify(sign(underpant's private key, 文件1), 文件2, underpant's public key) 會return false
要做到一個成功既signature scheme,最緊要就係無可能冒簽到
如果我用左個廢既signature, 又有個IQ180既連登仔想扮我既簽名
佢可以先收集好多個我既簽名,例如
文件1:「聽朝仲有8號風球我就切J」,underpants 簽名1
文件2:「聽朝仲有3號風球我就切J」,underpants 簽名2
....
文件n:「I go to school by bus」,underpants 簽名n
然後佢可能分析到文件同簽名既關係,破解呢個scheme
咁佢就可以試下sign 文件n+1: 「I am your father」,睇下佢有無方法起無我條private key既情況下都計到簽名n+1出黎
如果簽得arm既話,呢個signature scheme就可以收皮
private key,public key,同埋用private製造出黎既簽名, 其實都只係一串數字
都係好大好大好大好大既數
一條public key只會有一條相對應既private key
因為public key係由private key經過好複雜既數學方法生成出黎
簽名都一樣,係由private key同文件,經過數學方法產生。
要留意,拎住private key可以計到條public key出黎
但係拎住public key係無可能計得番private key
如果計得番既話,呢個digital scheme就收得皮啦
因為public key係全世界都可以知既
如果全世界都可以計得番你條private key出黎,咁就個個都可以扮你簽名啦。
「好複雜既數學方法」都有幾款,例如RSA, elliptic curve cryptography (ECC)
下面會介紹ECC
------文字解說完畢------
------對無興趣學數學既讀者黎講睇到呢度已經夠-----
首先講下private key
問:ECC既private key係點搵出黎架呢?
答:由1至2^256 入面random 揀一個數出黎
就係咁簡單。
當然你點樣random gen一條key 出黎都有好多學問既
如果你話你揀2做你條private key既話
無話唔得既,2真係起1到2^256之間
但係呢D咁簡單既key好容易就會比人破解到
用黎做例子就無乜所謂
跟住講下ECC既public key
elliptic curve cryptography就梗係有條curve啦
下面呢幅好似lin頭既野就係elliptic curve
!(elliptic_curve)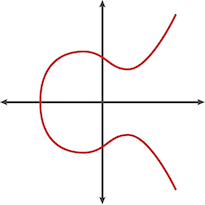
講點樣generate public key之前先講下定義
+呢個operator起唔同group入面既做法都唔係好同
咁起呢條憜圓曲線上面,點樣做「點同點既加法」呢?
例如想計P點+Q點,我地會先劃一條線連起PQ兩點
好似下面幅圖咁
呢條直線隨左經過P同Q,仲會起第三點cut過條curve
我地拎住第三點,水平反轉佢,得到R,就係P同Q相加既結果。
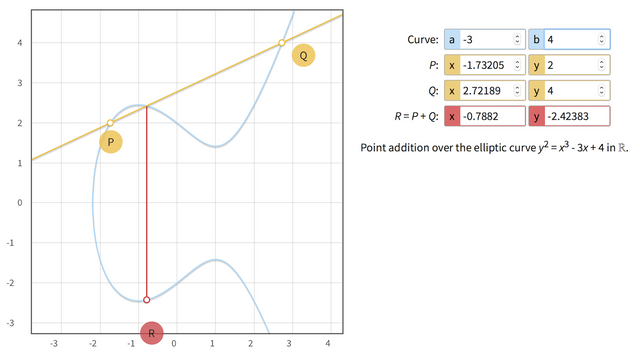
點解要咁加法?
因為起憜圓曲線上既加法既definition係:P+Q+R=0, where P/Q/R on the same straight line
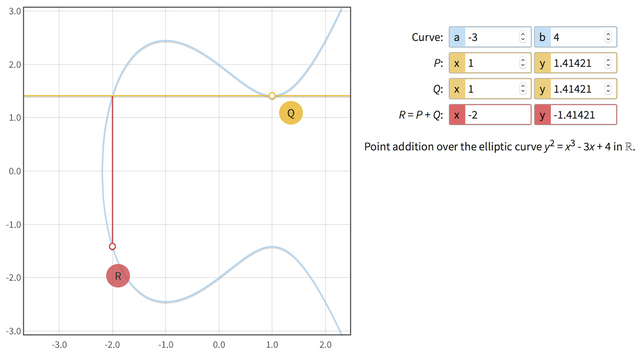
可能你會問,如果P同Q其實係同一點咁點算呀?得一點我點樣define一條直線?
如果有學過limit既概諗,你可以想像下Q點沿住條curve向P點越行越近
take limit之後其實就係條tangent line
就用呢條tangent line, 佢照樣會cut中條curve既另一點
反轉番果點就係P+P(或者Q+Q)既結果喇
好,而家大家知道
- private key
- addition on elliptic curve
有呢兩樣野就可以計到條public key出黎
起個lin頭上面我地揀一點做Generator Point, 即係G點
呢個G點要話比所有同你一齊用同一套digital signature scheme既人知
因為無左G點就verify唔到人地個簽名
點解G點會叫G點呢?因為我地拎住G點就可以generate曬其他點出黎
呢個唔詳細講啦,總之你就當大家公認左條curve上面其中一點好重要
起ECC入面,public key其實係一組(x,y)座標
public key既公式如下:
public key = private key * G點
起我地個例子入面private key 係2
所以
public key = 2*G點 = G+G
根住就可以套用剛剛學完既加法:
劃條tangent line on G, cut the curve at another point
反轉佢,做完!
用番上面幅圖,如果private key係2, G點既座標係(1, 開方2)
咁public key既座標就係(-2, -開方2)
實際上條private key唔會係2咁簡單,起碼都十萬九千七
所以你要計既可能係public key = 109700*G點=G點+G點+G點+G點+G點+G點+G點+G點+G點+G點+G點+G點+G點+G點.....
-----前方有進階數學-----
如果用上面既方法黎生成 public key, 就死梗
識少少數學既話你一睇就知可以調番轉佢黎計
即係拎住public key可以derive番private key出黎
因為elliptic curve on real plane係唔cryptographic secure
bitcoin真係用既elliptic curve其實又唔憜圓又唔係曲線
而係一堆點,條式係
y^2 === (x^3 + 7) mod p, where p = 2^256-2^32-2^9-2^8-2^7-2^6-2^4-1, 係一個超級大既質數
mod既意思係同餘,例如38===14 (mod 12), 因為38除12餘數係2, 14除12餘數又係2
所以38同14係同餘over 12
plot呢堆點出黎好似一堆symmetric noise咁:
起呢一大堆點上面計P點+Q點要點做呢?
淨係劃一條線連起P同Q點係唔夠既
要畫(ax+by+c) mod p === 0, 係一堆平行線
起呢堆平行線之間搵出第三點再水平翻轉(概念同curve既情況一樣)
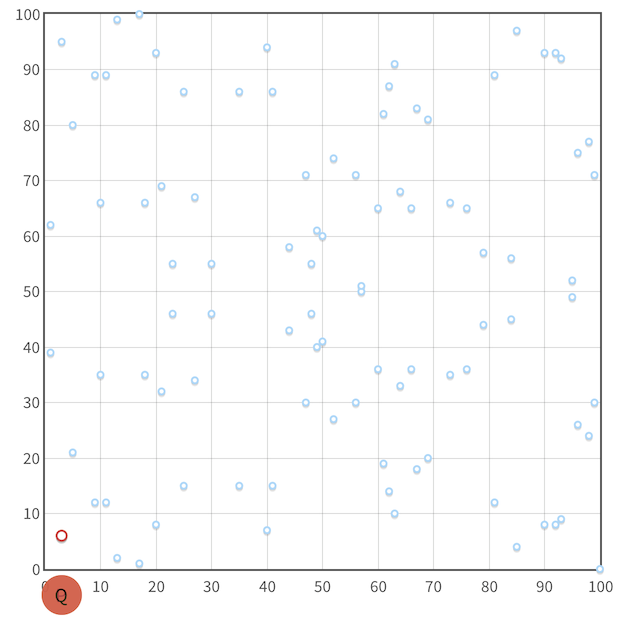
因為加左mod operator, 而且係一個超級大既質數
要起上面reverse engineer番條private key係好難好難好難既事
即係
given public key, G點: find private key such that: public key = private key * G點
咁你可能會話好簡單者,private key = public key / G點
elliptic curve上面既除法,又叫做discrete logarithm
問題黎喇,某種條件下既discrete logarithm係難到連數學家都諗唔到快既方法做
discrete log既難度係直情超越左RSA (based on large integer factorization)
即係話唔洗用咁多既bit數都提供到同樣既安全程度
就係因為discrete log係咁難解
我地先可以好安全咁比人知我地個public key,咁放心比人睇我地個簽名
同時又唔擔心佢地會估得番條private key出黎
------前方高能,數學恐懼人員請從速徹離-----
有public key, private key,就可以做digital signature入面最重要既一步:簽名
起generate 簽名之前我地仲要計一對暫時性既private key and public key
而家define
k = 暫時性private key
r = 由k gen出黎既暫時性public key既x coordinate
s = k^-1 * (Hash(文件) + my private key * r) mod p
where p = 2^256-2^32-2^9-2^8-2^7-2^6-2^4-1
(s,r)呢組數就我簽比呢份文件既簽名
當對家要verify呢個簽名,佢就要計
s^-1 * Hash(文件) * G + s^-1 * r * my public key
呢個結果係一組coordinate
如果佢既x-coordinate係等於r, 咁呢個簽名就係有效既
留意起呢條verify function入面只有我既public key
無我既private key起度
如果睇到你都無比上面堆怪獸嚇窒,仲睇得明同識得問
「點解條式要咁寫?」
「點prove佢地?」
「點解要揀果個p?」
可以reply問下,睇下有無數學系既高手肯回
再講落去就要更加深入認識憜圓曲線
要講algebraic structure, finite fields, subgroup order....
開多幾個chapter講都唔知得唔得
所以,真係有興趣既話,自己Google啦,有些路只能一個人走
-----數學部份完畢-----
咁public key private key起bitcoin上有咩作為呢
每一次你要動用你既bitcoin,都要用private key簽個名作實
起真係過數之前,server會check下你個戶口既public key同你個簽名夾唔夾
夾既,先比你動用果筆資金,validate呢次transaction
如果比人偷到你條private key,就可以冒認你簽發交易
下個chapter會詳細講
-----課外知識1-----
之前提過ECC既private key係random揀個數出黎
簽名時候用既k, 即係暫時性既private key同樣係隨機揀個數出黎
但係呢個k要揀得好小心:用過一次既k唔可以再用
如果你真係咁環保
文件1同文件2都用左同一個k黎簽名
咁就大件事喇:hacker可以根據簽名1同簽名2 計番你條private key出黎
即係比人破解左
點解咁特別提起呢個k?
因為歷史上真係有人試過用左同一個k而出事:Sony
PS3一直以黎係唔玩得翻版碟
當中就係用左ECC digital signature
每隻正版碟都有Sony既簽名,文件就係隻game
而且部console就有Sony既public key, 可以驗證 Sony既簽名
如果你自己寫左game,擺落PS3度行,因為你無Sony 既簽名,通過唔到認證,就行唔到隻game
PS3就係用左ECC digital signature
2010年George Hotz唔知點樣發現,Sony generate PS3 Game既簽名果陣無用到隨機暫時性private key (即係k)
反而,所有簽名都用左同一個k
咁只要你肯比錢買多幾隻正版碟
就可以有好多
文件1, Sony 簽名1
文件2, Sony 簽名2
文件3, Sony 簽名3
就可以搵到Sony簽名用既private key
然後用Sony既private key黎幫你自己寫既game簽名
Digital Signature scheme係唔會知邊人用private key黎簽
verify果陣淨係認數字,所以一但公開左條key,就全世界都可以冒認Sony簽名
即係可以繞過Sony既認證檢查
簡單黎講:Jailbroken,可以玩翻版碟
George Hotz公開左條key之後,Sony嬲到爆炸
決定從法律途徑告George告到甩褲
呢個行為辣著左Anonymous, 因為Anonymous覺得而家係Sony柒左
有人免費幫你搵個loophole出黎你唔多謝佢不突止,仲要告佢?
Apple iOS都成日比人jailbreak啦,你有無見過Apple告人?
所以2011年4月Anonymous大規模攻擊Sony
傳說話佢地就係用private key 簽左一個自己寫既programme,所以登入到dev-PSN network...
繼而拎到曬所有PSN所有user既資料...
之後既事大家都應該知啦,PSN down左成個月咁濟...
-----課外知識2-----
public key private key既用途仲有好多
例如網址分兩款: http同https
https多出黎個s係代表security, 佢secure在用左public key同private key既concept
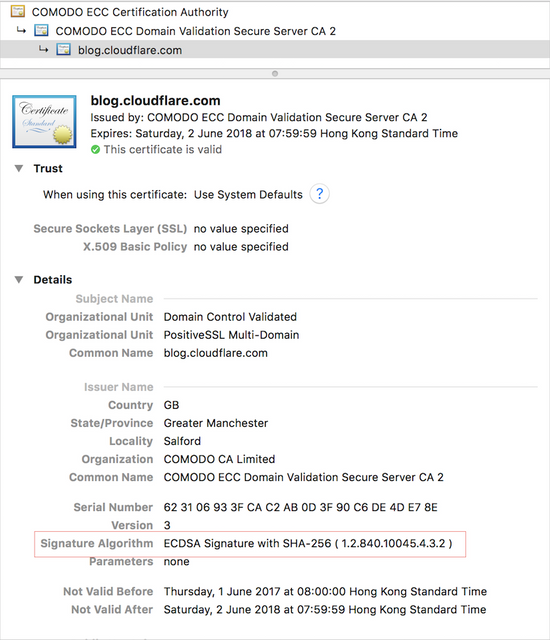
例如上圖
cloudflare就用左COMODO(certificate authority)既服務黎生產簽名
certificate authority既作用就係公信力極強既公司
即係CA話呢部server係恆生,佢就係恆生;CA話呢部server係渣打,佢就係渣打
你browser其實唔知邊個恆生邊個渣打,browser只係認CA
如果張cert係CA簽出黎既,browser就信佢係堅既
COMODO就用左ESCDA (elliptic curve digital signature algorithm) with SHA256黎生成佢張certificate
每個browser都內置左一個CA表
有時見到firefox同chrome會彈個紅色畫面出黎
話你將要瀏覽既網站不被信任(untrusted)
就係因為果D網站提供唔到一張CA簽發既證書,或者CA用左個好舊既方法(e.g. ESCDA with SHA1)黎簽證書
寫到尾,先發覺呢個chapter既數學好似重手得濟
唔知大家頂唔頂得順
打後既chapter唔會有咁多數,應該會易入口d
不過大家就算睇唔明/頂唔順,望過果堆數同圖,起碼大概感覺到密碼學同數學點樣環環相扣
數碼世界既安全隨左靠被選中既細路,更加緊要係數學基礎
雖然那些年講過「十年後,我連log是甚麼都不知道,照樣活得好好的。」
呢個世界真係需要班數撚去研究discrete log,我地先有咁先進而且安全既科技,仲有咁方便既生活。
所以數學家真係好偉大
亚克西!