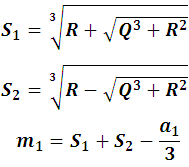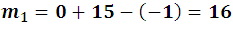This reminds me of the combinatorial theory, specifically a problem of variation. The question:
The product of three consecutive numbers is 3360. What are the numbers?
We can consider it as the number of variations of m elements taken n to n, is equal to the product of n consecutive and decreasing factors starting from , so that:

with the following data n= 3 y Vm,3= 3360. So:
It is clear that the cubic equations have 3 possible solutions, one of them is a real number, which is of our interest, therefore by the method of Cardano we can obtain this number:
with R= 1678, Q=-3/9 and a1=-3 we have:
In order for the variation to be fulfilled we have:
It is resolved. by @juancmz