[Answer and Winners] Mathematics × Programming Competition #8 [答案及得獎名單] 數學 × 程式編寫比賽 (第八回)

Mathematics × Programming Competition #8
Announcement of Answer and Winners

^{Designed by @nicolemoker}

For Chinese version please scroll to the bottom. 中文版請見文末。

Question

Ken has a four-digit calculator which displays numbers using the seven-segment-display. For example the number 159 is displayed as

Note that 159 is displayed as 0159

Suppose we want to use non-transparent cards to represent all the possible 4-digit numbers from 0000 to 9999. Each card will show one 4-digit number, where the numbers are written using seven-segment-display. However when some cards are rotated 180°, a new number can be formed. For example when the card 0159 is rotated 180°, it becomes 6510.

Note that it is acceptable for the ‘1’ to be displayed on the left hand side

Considering the possibility of rotating a card 180°, what is the minimum number of non-transparent cards required to represent all the possible 4-digit numbers from 0000 to 9999?

Answer: 8824

Mathematical approach

Among all digits, only ‘0’, ‘1’, ‘2’, ‘5’, ‘6’, ‘8’ and ‘9’ can be rotated, which would form ‘0’, ‘1’, ‘2’, ‘5’, ‘9’, ‘8’, ‘6’ respectively.

First of all, there are 7⁴ = 2401 4-digit numbers which can be rotated to form a meaningful number.

Among these 2401 numbers, there are 7² = 49 4-digit numbers which can be rotated to form the original number. This is because the first 2 digits of the number will determine the remaining 2 digits.

Therefore there are 2401 - 49 = 2352 numbers which can be rotated to form a new number. Each pair of numbers can help us to save one card.

So we only require 10000 - 2352 / 2 = 8824 cards.

Programming approach

The logic of a programming solution would be quite similar to the flow above, except the counting will be done by program instead of maths.

Psuedocode:

Define the rotation mapping for digits 0, 1, 2,... ,9
Counter = 0  // for storing number of 4-digit numbers which can be rotated to form a new number
For number = 0000 to 9999
    Rotate the number
    If the new number is meaningful and different from original
    Then counter+1
Loop
Output 10000 - counter / 2

Solutions written by other participants

Author	Article
@speeding	Solving with one line of Python script!
@speeding	Solving with C#
@leedslemon	Solving by Excel
@vincentyip	Solving by JavaScript
@tvb	Solving by PHP / Maths
@armandocat	Solving by JavaScript
@justyy	Solving by JavaScript
@breathewind	Solving by Qt
@firstamendment	Solving by Java

Winners

Among 32 participants, there are 20 people who got the correct answers. Thank you for your participation!

@armandocat @challk @vincentyip @nanosesame @victorier @daut44 @justyy @kona @aaronli @john811 @heimindanger @tvb @cifer @breathewind @victory622 @firstamendment @doughtaker @nahaha @tensaix2j @biuiam @krischy @speeding @leedslemon @jeffreytong @ghasemkiani @thomaskikansha @wilkinshui @guyverckw @mcw @gladyslui @connieleung @rfece143

SBD payout of the the question post = 30.123 SBD

Besides, @steemstem has generously sponsored 15 SP, 10 SP and 5 SP for the first, second and third prizes!

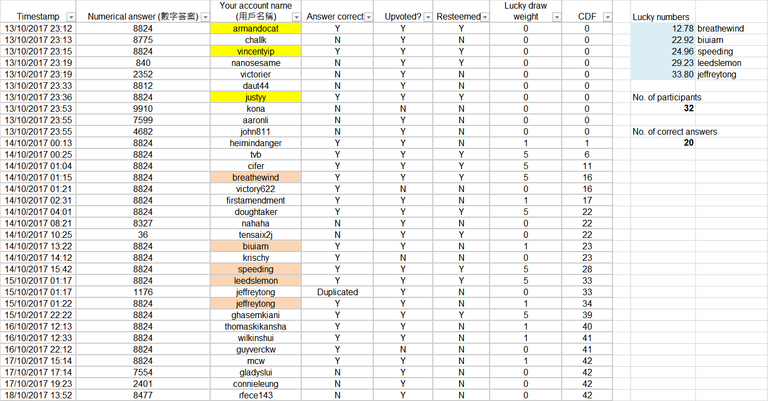
The winners and prizes are tabulated below:

Winner	Prize	SBD
@armandocat	First prize	30.123 / 8 = 3.765 SBD + 15 SP
@vincentyip	Second prize	30.123 / 8 = 3.765 SBD + 10 SP
@justyy	Third prize	30.123 / 8 = 3.765 SBD + 5 SP
@breathewind	Consolation prize	30.123 / 8 = 3.765 SBD
@biuiam	Consolation prize	30.123 / 8 = 3.765 SBD
@speeding	Consolation prize	30.123 / 8 = 3.765 SBD
@leedslemon	Consolation prize	30.123 / 8 = 3.765 SBD
@jeffreytong	Consolation prize	30.123 / 8 = 3.765 SBD

Congratulations to the winners!

The steemSTEM project (@steemstem) is a community-supported project aiming to increase the quality and the visibility of STEM (STEM is the acronym for Science, Technology, Engineering and Mathematics) articles on Steemit. Please support steemSTEM by following @steemstem and joining the chat channel. You can also consider joining a private curation trail to further support steemSTEM by asking about it in the chat channel. In order to further promote the use of the chat channel, I will stop announcing the time of next competition via a post. Instead I will announce the time in advance in the chat channel!

數學 × 程式編寫比賽 (第八回)
答案及得獎名單公佈

^{Designed by @nicolemoker}

問題

Ken有一部只能顯示四位數的計算器，它使用七段顯示來顯示數字。例如，159顯示為

注意159顯示為0159

假設我們要使用非透明卡紙來表示從0000到9999所有可能的4位數字。每張卡紙將顯示一個4位數字，而這些數字是使用七段顯示器所寫成的。留意當某些卡片旋轉180°時，可以形成新的數字。例如當卡片0159旋轉180°時，它將變成6510。

注意'1'顯示在左側亦可接受

考慮到將卡紙旋轉180°的可能性，最少需要多少張卡紙才能表示從0000到9999所有可能的4位數字？

答案: 8824

數學方法

在所有數字中，只有 ‘0’, ‘1’, ‘2’, ‘5’, ‘6’, ‘8’ 及 ‘9’ 能在旋轉後產生有意義的數字，分別為 ‘0’, ‘1’, ‘2’, ‘5’, ‘9’, ‘8’ 及 ‘6’。

首先，共有 7⁴ = 2401 個4位數字可以旋轉至形成一個有意義的數字。

而在這2401個數字中，有 7² = 49 個4位數字可以旋轉至形成原本的數字。這是因為號碼的前2位數字將決定剩餘的2位數字。

因此，共有2401 - 49 = 2352 個4位數字可以旋轉至形成一個新的數字。每對數字可以幫助我們節省一張卡。

所以我們只需要10000 - 2352/2 = 8824張卡。

編程方法

編程方法的邏輯與上述流程非常相似，只是計算可能組合將由程序而不是數學方法完成。

偽代碼:

定義0-9數字旋轉後會產生哪些數字 
Counter = 0  // 用於儲存有多少個數字可以在旋轉後形成新數字
For number = 0000 to 9999
    旋轉該數字
    如果新的數字是有意義且不同於原來的
    Then counter+1
Loop
輸出 10000 - counter / 2

由其他參賽者提供的答案

作者	文章
@speeding	以一行Python script 求出答案！
@speeding	以C#求解
@leedslemon	以Excel求解
@vincentyip	以JavaScript求解
@tvb	以PHP或數學方法求解
@armandocat	以JavaScript求解
@justyy	以JavaScript求解
@breathewind	以Qt求解
@firstamendment	以Java求解

得獎者

在32個參加者之中，有20人答對。多謝大家的熱烈參與！

比賽題目帖文的SBD收入 = 30.123 SBD

另外，@steemstem 慷慨贊助了15 SP、10 SP以及5 SP予是次比賽的第一、二及三等獎！

下表顯示得獎者及其所得獎金：

得獎者	獎項	SBD
@armandocat	一等獎	30.123 / 8 = 3.765 SBD + 15 SP
@vincentyip	二等獎	30.123 / 8 = 3.765 SBD + 10 SP
@justyy	三等獎	30.123 / 8 = 3.765 SBD + 5 SP
@breathewind	安慰獎	30.123 / 8 = 3.765 SBD
@biuiam	安慰獎	30.123 / 8 = 3.765 SBD
@speeding	安慰獎	30.123 / 8 = 3.765 SBD
@leedslemon	安慰獎	30.123 / 8 = 3.765 SBD
@jeffreytong	安慰獎	30.123 / 8 = 3.765 SBD

恭喜所有得獎者！

steemSTEM（@steemstem）是一個由steemit社群支持的項目，旨在宣傳STEM（STEM是科學，技術，工程和數學的首字母縮略詞）。請追蹤 @steemSTEM 以及加入聊天頻道來支持steemSTEM。你還可以透過加入自動點讚系統來在為了進一步支持steemSTEM，詳情請在聊天頻道內向負責人士查詢。為了推廣聊天頻道的使用，我將不再透過發文來宣布下一場比賽的時間，我會在聊天頻道中提前公佈比賽時間。