Okay. Let's get started. The first person to solve the word problem below will get an upvote worth $0.5. There will also be some consolation upvotes for some of the late comers.
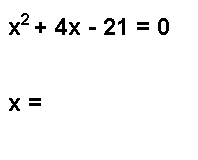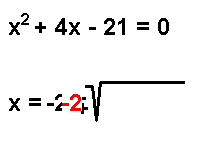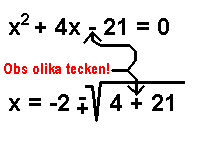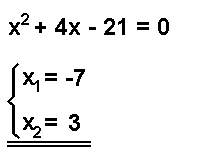
How To Participate:
Kindly UPVOTE this post and then answer the question which follows in the comment section. Entries that do not comply with this simple rule will be disregarded.
Question:
A thief is in a house to steal paintings but finds 94 different ones. He knows that there is 5 expensive paintings and he can only carry 5 paintings. Can you calculate for the thief, what are the odds of him stealing 1 expensive painting?
Deadline:
The test comes to an end once a winner emerges or at the expiration of this post. Good luck guys.
Thanks for visiting this channel @steemitcentral. Use the "steemitcentral" tag in your Steemit or crypto-related posts and get rewarded with some upvotes.

X=3
32+(4.3)-21=0
5.3% is the probability of an expensive painting, since this is calculated by dividing the total number of paintings by the number of paintings you will carry, this is the definition of probability.
Not really, Hint: when he picks the first painting, he has 5/94 chance to get a expensive one. What about pick 2?
A thief is in a house to steal paintings but finds 94 different ones. He knows that there is 5 expensive paintings and he can only carry 5 paintings. Can you calculate for the thief, what are the odds of him stealing 1 expensive painting? Look, it's just a painting.
haha ture :)
The probability is of 1.06%
No, when he picks the first painting, the odds is 5/94 = 0.053....= 5,3% then he picks 4 more :)
5.3% represents the 5 expensive paintings of the 100% paintings (94 cans).
It also represents picking 1 from the mix of 5 expensive and 89 cheap, that is the first pick! 5/94 is the odds of picking 1 expensive in the first pick out of 5 picks.
Every pick after pick 1 , will give higher odds, it is much higher !
(5/94) x 100 = 5,318%
That is if he picks 1 painting :) he will pick 4 more
I do not understand. ?
I think it's 94 at least 1 be the one of great value
Yeah 5 out of 94 is valuable, and the thief will steal 5 random ones, what is the odds that he gets 1 of the valuable!
Yes, but because it is random, the thief can not choose the 5 expensive ones. By dividing 5/94 we are assuming that at least one of them is the valuable one.
Yeah that is the odds of picking 1 valuable in 1 pick... The thief does have 5 picks, thereby much higher odds!
Another alternative would be 1 / (94-4). But I see it very idealistic. There is no randomness. Since I am ensuring that I choose only one face and leave the rest. But I can not know how to do it. And the rest is still part of the sample population