Figure 1.2 Because the number of input numbers exceeds the output, we are sure that at least one output must be done for the map of multiple input maps of the hash function.
Now, to make things worse, we said it was impossible to find clashes. Nevertheless, there are methods that are sure to find a collision. Consider the following general procedure for the collision of a hash function with a 256-bit output size: Select 256 + 1 individual values, each calculate hash and check whether any two outputs are equal. Since we have more input than the possible outputs, so when you apply the hash function, some of the pairs should take place.
The above method is guaranteed to find a collision. But if we calculate random inputs and calculate hash values, we will encounter conflicts with high probability before testing 256 + 1 inputs. In fact, if we randomly prefer only 130 130 inputs, it is 99.8% likely that at least two of them will face their collision. Due to the probability of the probable possible probability of possible outputs, we often find out the collision by examining birthdays as paradox. At homework questions at the end of this chapter, we will examine this in more detail.
This collision detection algorithm works for each hash function. But, of course, the problem is that it takes too much time to do this. For the hash function with a 256-bit output, you have to count the hash function in the worst case of 256 + 1 times and about 28 times. This is a big number of astronomers - if the computer calculates 10,000 hash per second, it takes one October (10 27 years) to calculate 128 hashs! For another way to think about this, we can say that every computer created by humanity was computing from the beginning of the entire universe, but so far, the clashes that they took were still the smallest. Less is the way that the world will be destroyed by a giant meteor in the next two seconds.
We have thus seen a common but reflexive algorithm to find a collision for a hash function. The more difficult question is: can you use a hash function in a special way for any collision? In other words, although the generic collision detection algorithm is not usable, there may still be some algorithms that can detect collision skills for a specific hash function.
For example, consider the following hash function:
H = x 256
(X) mod 2
This function meets our requirements for a hash function because it accepts input of a length, returns a specific size output (256 bit) and is efficiently computable. But this function has an effective method to find out a collision. Notice that this function only returns 256 bits to the end of the input. Then there would be a clash value of 3 and 3 + 2 256. This simple example explains that even though our generic collision detection method is not usable in practice, there are at least some hash functions for which effective conflict detection mechanism exists.
Yet for other hash functions, we do not know if such methods exist. We suspect that they are in conflict prevention. However, there are no hash functions that have proven conflict resistant. For the cryptographic hash function that we rely on in practice, only the functions that really tried, the clashes are really hard to find and have not yet succeeded. In some cases, such as the old MD5 hash function, after a few years there was a collision, abandoning the function and progressing gradually beyond practical use. And so we believe that those conflicts are resistant.
Applications: Message Digesters Now we know what is a conflict-resistant question: What is useful for conflict-resistance? Here's an application: If we know that two inputs x and y have a conflict-resistant hash function in H has different hash,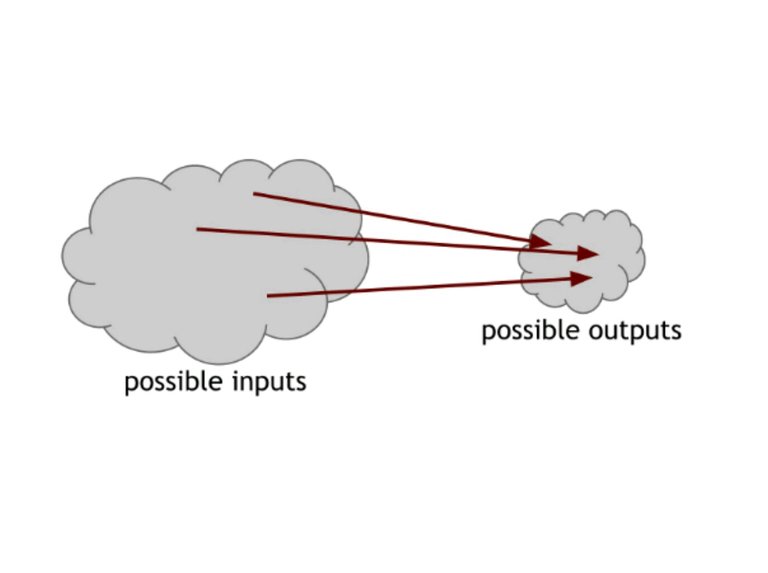
Sort: Trending