Consider the following thought experiment put forward by Daniel Kahneman in his book “Thinking, Fast and Slow”:
-Consider a 50–50 gamble in which you can lose $10. What is the smallest gain that makes the gamble attractive? If you say $10, then you are indifferent to risk. If you give a number less than $10, you seek risk. If your answer is above $10, you are loss averse.
-What about a possible loss of $500 on a coin toss? What possible gain do you require to offset it?
-What about a loss of $2000?
Kahneman found that for most people, the amount possible to win had to be in the range of 1.5–2.5 the amount possible to lose for a 50–50 gamble to appear attractive . As traders, we are thought to think differently about these sort of scenarios. If we can identify even a small edge, we are going to take that bet, and we are going to take it as many times as we can as long as it exists. So if someone offers me a 50–50 coin toss gamble where I lose $100 every time it turns out tails but I gain $105 every time it turns out heads, I am immediately speculative about the coin and the person. But if I can flip and choose the coin, then I will take this bet and I will continue to flip this coin while the bet stands. I might even hire somebody to flip this coin for me. But an interesting thing happens as the stakes grow. We need to be more cautious and prudent as the risk of ruin looms larger. Therefore, the amount required as a gain in relation to the loss has to grow. At a certain point, we will no longer take this bet no matter how attractive the gain as it just no longer makes sense. But how do we determine what is a good amount to stake when you have an identifiable edge to maximise capital growth and minimise going bust. As with most questions that have no clear answer, multiple approaches have been offered.
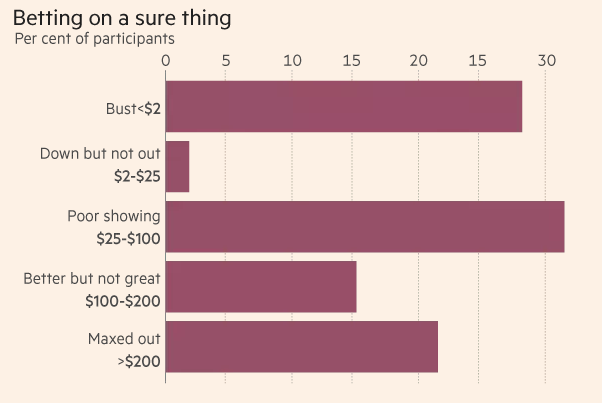
One possible solution is the Kelly Criterion. This method has been praised by both Edward Thorp and Warren Buffet. I first became aware of the Kelly Criterion when I read a coin flip experiment conducted by Victor Haghani of Elm Partners and Richard Dewey. Players in the experiment which consisted of MBA students and investment professionals were given $25 of real money and had 30 minutes to bet on a coin flip game where they were told that the coin had a 60% of coming up on heads every time. They could bet however much they wanted each time and the goal was to maximise their money by the end of the 30 minutes. Payouts were capped at $250 so they had a real incentive to try and increase their initial $25 stake. Shockingly, 79% failed to reach the $250 mark and even 28% went bust!
The Kelly criterion holds that you bet a constant proportion of your money each time. The proportion is determined by the edge. So, in this experiment where there is a 60% chance of the coin ending up on heads, the proportion to be bet on each flip is determined by multiplying the probability of win by two and subtracting one. So in this case, it equates to 20% of remaining capital on each flip (0.62–1 = 0.2). If the coin had a 90% chance of ending on heads, the amount of capital to be bet on each flip would be 80% (0.92–1 = 0.8). The amount of capital to be staked often can be large when based on the Kelly Criterion so a popular alternative is the half Kelly where you stake half the amount which is proposed to be staked by the Kelly Criterion. The problem with applying these to trading is the edge can only be estimated. Therefore, estimates of an edge should be conservative.
Because estimates of an edge are uncertain, other traders recommend certain techniques for staking. Paul Tudor Jones recommends in Market Wizards to not bet any more than 1% of capital on any given trade or more than 3% on any collection of trades at any given time, thereby minimising the worst impact to the portfolio. There is also the recommendation that when on a streak of losing trades, to minimise the portion of capital being staked, and then increase it when back on a streak of winning trades. This makes sense as it is possible that when on a streak of losing trades, that your edge is being inaccurately estimated.
(1) https://www.goodreads.com/book/show/11468377-thinking-fast-and-slow
(2) https://www.ft.com/content/7cd9b6c8-9cd7-11e6-8324-be63473ce146
(3) https://www.goodreads.com/book/show/966769.Market_Wizards
Good article, I've used the Kelly formula in the past but abandoned it because my systems fell outside the criteria of my maximum risk amount a lot of the time.
Example, a system is 40% winners with a 5:1 reward, Kelly suggests using 28% capital risk on each trade... a little too scary lol.
One day I'll get round to plotting it, but there seems to be a narrow range of win probability and risk reward ratios that end with realistic risk levels for trading, like 1 or 2%.
I think the Kelly system is optimised for probability of 50:50 like a coin toss, when you start changing the R:R it wildy skews the values.
Resteeming, because I love all things probability !
WARNING - The message you received from @biplobmollik is a CONFIRMED SCAM!
DO NOT FOLLOW any instruction and DO NOT CLICK on any link in the comment!
For more information, read this post: https://steemit.com/steemit/@arcange/phishing-site-reported-upperwhale
Please consider to upvote this warning if you find my work to protect you and the platform valuable. Your support is welcome!