I wasn't able to find any analysis of the inflation rate for the SmartCash SMART cryptocurrency so I decided to try and do some of my own analysis. Hopefully my work is accurate, and hopefully some of you will find it helpful.
The rate that new SmartCash (SMART) is created is specified on https://smartcash.cc/what-is-smartcash/ where it says that the "BlockReward = 5000*143500/BlockHeight" with a maximum of 5000, and a Blocktime of 55 seconds.
Per http://explorer.smartcash.cc, I found that the current BlockHeight was 201866, and when I plugged that into the equation above I calculate that roughly 3554 SMART should be created in block 201886 which checks out with what I saw on the explorer link above. Also, at block 201886 the total supply was listed on the explorer link as 965150963 so we can calculate the inflation rate of block 201886, however, what I think would be most helpful would be to calculate the monthly inflation rates from one 25th of the month to another because that is when SmartRewards are calculated. A script could be written to do this, but I decided to use calculus and a spreadsheet instead.
The equation, BlockReward = 5000 * 143500/BlockHeight, is basically a function of the form f(x)=A/x where A is a constant (which equals 5000 * 143500) and x is the BlockHeight, and from calculus you have the integral of this function taking the form "A * ln|x| + C" where ln|x| is the natural log of the absolute value of x (where the natural log is the log of base e where e is 2.71828) and where C is another constant, and we can determine the constant C from a known data point like the one in the paragraph above where the total supply on block 201886 was 965150963. The resulting equation for the total supply of SmartCash (SMART) as a function of BlockHeigth is as follows (valid for blocks >= 143500).
total supply of SMART = 5000 * 143500 * ln(BlockHeight) + 965150963 - 5000 * 143500 * ln(201886)
Below is a graph of the total SmartCash (SMART) supply from 11/25/2017 to 12/25/2019.
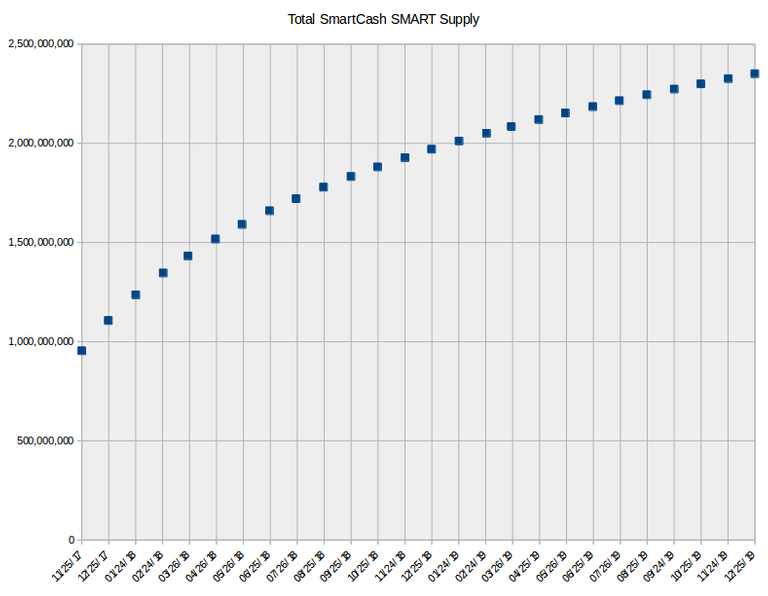
Using the equation above, and using the explorer to find a block that occurred on the 25th of November 2017, block 198756, and assuming blocks are created roughly every 55 seconds, I used a spreadsheet to calculate the following table which shows the total supply of SMART on the 25th of the month for several months, and I also shows the monthly inflation rate of SMART.
| Day | Total Supply (SMART) | Monthly Inflation |
|---|---|---|
| 25 Oct 2017 | 752,731,452 | |
| 25 Nov 2017 | 953,939,853 | 26.73% |
| 25 Dec 2017 | 1,106,608,771 | 16.00% |
| 25 Jan 2018 | 1,236,260,037 | 11.72% |
| 25 Feb 2018 | 1,346,030,241 | 8.88% |
| 25 Mar 2018 | 1,432,534,959 | 6.43% |
| 25 Apr 2018 | 1,517,521,797 | 5.93% |
| 25 May 2018 | 1,591,170,372 | 4.85% |
| 25 Jun 2018 | 1,660,080,636 | 4.33% |
| 25 Jul 2018 | 1,721,004,357 | 3.67% |
| 25 Aug 2018 | 1,778,955,560 | 3.37% |
| 25 Sep 2018 | 1,832,573,925 | 3.01% |
| 25 Oct 2018 | 1,880,906,206 | 2.64% |
| 25 Nov 2018 | 1,927,648,422 | 2.49% |
| 25 Dec 2018 | 1,970,156,460 | 2.21% |
| 25 Jan 2019 | 2,011,586,125 | 2.10% |
| 25 Feb 2019 | 2,050,753,600 | 1.95% |
| 25 Mar 2019 | 2,084,381,896 | 1.64% |
| 25 Apr 2019 | 2,119,862,309 | 1.70% |
| 25 May 2019 | 2,152,604,491 | 1.54% |
| 25 Jun 2019 | 2,184,938,100 | 1.50% |
| 25 Jul 2019 | 2,214,899,744 | 1.37% |
| 25 Aug 2019 | 2,244,599,337 | 1.34% |
| 25 Sep 2019 | 2,273,118,279 | 1.27% |
| 25 Oct 2019 | 2,299,678,241 | 1.17% |
| 25 Nov 2019 | 2,326,128,197 | 1.15% |
| 25 Dec 2019 | 2,350,828,782 | 1.06% |
One way the table above may be helpful could be to compare your monthly SmartRewards to that month's SMART inflation rate. For example, if your SmartRewards on 25th of January 2018 are 5% then your rewards would be less than the 11.72% inflation. Does anyone know where you can go to see the percentage SmartRewards ends up paying out each month? Maybe I should I just buy 1000 SMART and hold it to find out what the SmartRewards rate is each month :)
Another way the table above can be helpful is it can help explain why your SmartRewards will decline over time because inflation declines over time and your SmartRewards are based on inflation. I think only 15% of SMART's inflation goes toward SmartRewards.
Hopefully the table above is accurate. I double checked it, but I didn't triple check it. Please let me know if you notice any errors.
@smartbot tip @twodollars 100
This is pretty cool! Thanks for the effort :)
Σ$$$ Tipped @twodollars
Σ100 SMART! Comment@smartbot helpto claim. Currently the price of SmartCash in the market is$0.058 USDperSMART. Current value of the tip is$5.80 USD. To find out more about SmartCash, please visit https://smartcash.cc.@smartbot help
You can use the following commands:
balance- displays your current wallet balanceaddress- displays your deposit addresswithdraw <address>- withdraws your whole wallet balance to specified addresstip <nick> <amount>- sends the specified amount of smartcash to nicknameterms- displays terms and conditions for using @smartbot@smartbot balance
@twodollars has
Σ100 SMART(unconfirmed:Σ0 SMART).@smartbot address
Your deposit address is
SP1LFtbrowMug4HXTcb1LYa8raJ8LThdXw.@smartbot withdraw SbH4VXcvDDLT6VX2oyJbK4qhwyJ2yv6HjC
Thanks for posting this via ChainBB (I would have missed it otherwise).
Have you posted a link to this in the discord? I bet some of them wouldn't mind jumping in and explaining things a bit more.
Thanks, I'll plan to post a link in the smartcash discord. It was your post about smartcash that got me looking more into it.
Inflation rate decrease means price go higher overtime. And since the 5,000,000,000 coin is design to mine 100 years, I think Smart is one of the most stable coin.
Having a decreasing inflation rate doesn't necessarily mean that prices go higher over time. However, it does mean there is less SMART awarded to miners over time, less SMART given as SmartRewards over time, and less SMART given to SmartHive/HiveTeams over time. The hope is that decreasing inflation will increase the demand for SMART resulting in SMART becoming more valuable over time, but this isn't guaranteed to happen.
Nice article. This information is really helpful.
Great effort, and very good information. Are you an economist or something?
Thanks for the help, very good publicity.
Nice and informative, Thanks :)
Thanks!