What is zkSNARKs: Spooky Moon Math

What is zkSNARKs: Spooky Moon Math. With Ethereal entered a phase of Metropolis, he would introduce the various changes that will make it more abstraction and privacy-friendly. One of those changes is the introduction of "Zero-Knowledge Interactive Arguments concise Non-knowledge" aka Zk-Snarks. ZK-Snarks runs based on the notion of zero knowledge.

In this article, we will discuss the idea of zero knowledge and its application in the technology of blockchain.

What is zkSNARKs: Spooky Moon Math

Zero Knowledge proofs appear in the 1980s thanks to the work of researchers at MIT, Shafi Goldwasser, Silvio Micali, and Charles Rackoff. They are working on issues related to interactive proof systems, in which a Prover exchanging messages with the Verifier (more about checklists and measuring later) to convince them that they have knowledge of specific evidence without stating what that knowledge.

Before making their landmark discovery, most systems are based on evidence of the nature of the "health" of the system of evidence. It is always assumed that the "comparison" could be dangerous in a scenario where they will try to fool the verifier. The third researcher is flipping that notion on its head by questioning the morality of the verifier and not a comparison. The question they ask is, how can anyone know for sure that the verifier will not divulge knowledge and there are also concerns about the amount of knowledge about the proof which will be known to pengverifikasi during the verification process.

There are a variety of real-world consequences of this puzzle and one of the most famous has to do with password protection. Suppose you want to login to the website using your password. The standard protocol is that the client (you) will write in words the password and send it to the server, the server will then enter the password and match it with the hash they save on their system. If the value is appropriate, then you can get into the system.

Can you see the great deficiencies in this system right? Can you see the great deficiencies in this system?

The server has a version of the plaintext of your password, and your privacy are under the mercy of the server (the verifier in this scenario). If the server is compromised or attacked, the word password will be with the evil party and as a result can be quite awful. To address this scenario, there is no evidence of knowledge that is absolutely vital and breaking the line in all things.

There are two parties when it comes to zero knowledge proof (as stated above), the comparison and verification. Zero knowledge States that a themselves can prove to voters that they have the verification of specific knowledge without telling them what the actual knowledge that.

Properties of zero knowledge proof

In order for the ZKP work need some specific parameters:

-Completeness: If the statement was true then the honest verifier can be assured by an honest reformer.
-Voice: If a comparison were not honest, they could not convince the verifier on health that statement with a lie.
-Zero-Knowledge: If that statement is true, the verifier will not know what exactly the statement.

So now we have a basic idea about the zero-knowledge proof, let's see a few examples before we dive deep into zk-snarks and its application in blockchain.

Case # 1 the cave Alibaba

In this example, the reader (P) told the verifier (V) that they know the keywords from a secret door at the back of the cave and they want to prove it to the verifier without actually tells them the word password.

So that's how it looks:

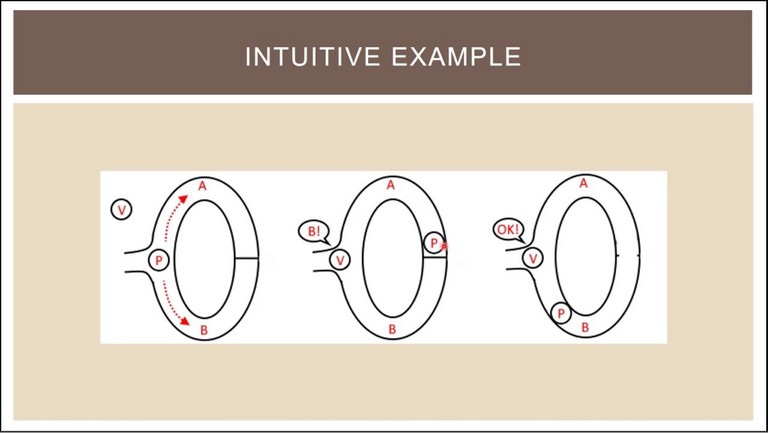
Image courtesy: Scott Twombly (YouTube channel)

Prover lowers one of lines A and B, suppose they had originally decided to skip A line and reach secrets behind the door. When they do, the verifier V sign in the entrance, without knowledge of the actual Street where taken by readers and stated that they would like to see the comparison appear from line B.

In the diagram, as you can see, the comparison is indeed appearing on line B. But what if this is a dumb luck? What if pembuktinya not knowing the course code, and take the road B, stuck in the door and with sheer luck, the identifier telling him to get out of line B, originally they were living?

So, to test validitasnya, an experiment was performed many times. If the comparison can appear on the right track at all times, this proves that the verification of voters really know which password though pengenalnya not know what exactly the password.

Let's see how these three properties of zero knowledge satisfied in this example:

-Completeness: because that statement is true, honest reformer to convince the honest verifier.

-Sound: If the comparison is not honest, they can't fool the verifier because the test was performed many times. Finally, the comparison must be luck runs out.

-Zero-Knowledge: Verifier never know what password, but assured that the giver has had it

Case #2 Finding Waldo

Remember finding Waldo ?

Of course, you would have seen it somewhere, either in the real world or online. For those who don't know, Finding Waldo is a game where you must find the "Waldo" among a sea of humans. This is our game "Spot the guy" that simple. Just to give you a basic idea, here's the game:

Image courtesy: Youtube (IntoConnection)

And the idea is to find Waldo that looks like this:

Image courtesy: Pinterest

It seems pretty straightforward right? Find this person among a sea of other people that you see in the game. OK, so where did the concept of Zero Knowledge go into here? Imagine there are two Anna and Carl. Anna tells Carl that he knows where Wally is but she doesn't want to show where exactly she was. So, how she can prove to him that she had found Wally without showing the exact position?

There, a work interesting by Naor, Naor and Reingold which shows two Zero Knowledge Solutions to this problem. There is a "Mid-Tech Solution" and "low-tech" Solution. Let us discuss both.

Mid-Tech Solution

The reason why this solution is "mid-tech" is because our gauge props and require access to the photocopier to make this work. So that's how it goes. First, Anna and Carl will make a photocopy of the original game. Then Anna, while making sure Carl isn't looking, will cut Waldo of photocopying and then destroy the rest of the food. After that he could show to the Waldo to Carl and prove that she knows where Waldo Chase everything without indicating precisely to Carl.

There is a problem with this solution. Even though it meets the criteria of "zero-Knowledge", these criteria do not meet the criteria of "health". There are many ways that can be rigged Anna here. He could just have a random cut Waldo with him since the beginning and can only show it on Carl without really know where Waldo is. So what is the solution?

The solution to this is meticulous and thorough testing. First, Anna and Carl will take photocopy of the game. Then Carl will draw a distinctive pattern on the back of photocopying. After that, Carl will accompany Anna to a room where he will be isolated and did not have a chance to do any cheating. If Anna came out as Waldo, then Carl can be sure that he really knows where Waldo without disclosing the solution. They can repeat this experiment several times and Carl can compare different cutouts Waldo for more confident again about the validity of the claim of Anna.

Low-Tech Solution

This solution requires very basic equipment. The idea is simple only. Get a large, cardboard measuring twice as much of the game and cut into small squares on it. Well, when Carl does see, Anna could move the kartonnya to the game such that the length of the rectangle right on top of Waldo. Now, he can tell Carl to look around and it is what he saw:

Image Courtesy: Applied Kid Cryptography by Naor And Reingold

So, while Carl may get a very basic idea about where Waldo is, he actually did not know the exact location. Anna has proven to Carl that he knows where Waldo without showing the location exactly.

Case #3: Sudoku

Another great app from zero knowledge exists in the Sudoku. For those who don't know, Sudoku is the puzzle of Japan where you get 9X9 table that looks like this:

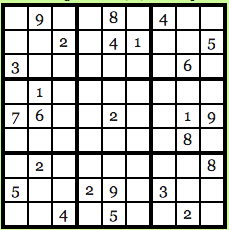
Image courtesy: Computational Complexity Blog

The idea is to fill each row, each column and each 3 x 3 block with number 1-9 and no number to repeated himself. So, the solution to the puzzle above looks like this:

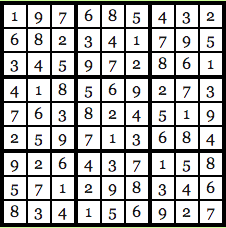
Image courtesy: Computational Complexity Blog

As you can see, each row, column, and 3 x 3 block is unique and there is no one number that has been repeated. Let's go back to our old friend Anna and Carl. Anna has found a solution to a Sudoku puzzle and Carl, was skeptical that he did not believe it and wants to prove that he did Anna know the solution. Anna wanted to prove their honesty, but at the same time, he doesn't want to figure out the right solution from Carl Riddle. How is he going to do it? Anna will use Zero Knowledge to prove the validity of his claim.

First, Carl Sudoku solutions will run through a computer program that has been verified, to be honest and the program will run the figures through the substitution of the substitution is selected randomly. Say, for this particular issue, the password of the selected program is:

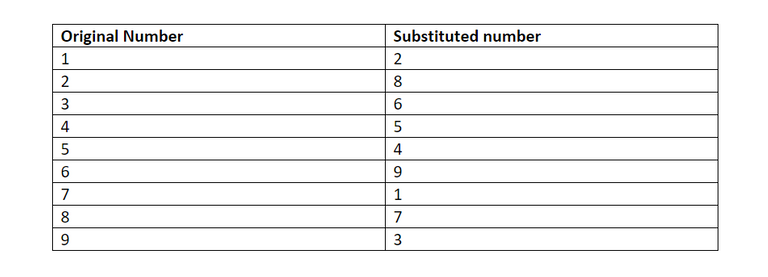
The chosen program and cipher is such that each digit has the same chance of being transmuted into its substitution as any other number. Basically, 1 has as much chance of being transmuted as 3 and 4 have as much chance of being transmuted as 9 and so on and so forth. So, using this cipher gives us the following solution to the puzzle above:

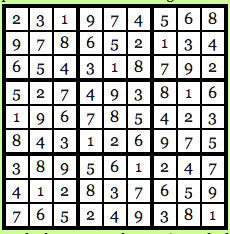
Image courtesy: Computational Complexity Blog.

Anna got a solution of transmutation is now, remember that Carl still does not know the original solution and he also has no solution of transmutation. So, what do the current Anna is that he hides all numbers in the puzzles by using the mechanism of the "lockbox", basically Carl will not be able to see any figures and will see the empty 9X9 box in front of him.

Carl now has 28 options in front of him:

-Says one line.
-Reveal a column.
-Disclose your 3 x 3 box.
-Reveal version of original puzzles transmuted.

Suppose Carl wants to know what the third row looks like:

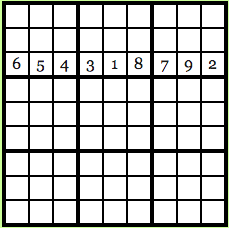
It is what he saw. Carl will see that every number in the line and it is unique because every number that may exist in the original solution has an equal probability to be emitted through the cipher, Carl would not know what the solution is.

Now suppose, Carl decided to take the latter option and wanted to see what it looks like when it is transmitted to the original puzzle:

Once again, due to the cipher is selected at random and all numbers has an equal probability to mentransmutasi, Carl wouldn't know a solution first. Carl can now undergo all 28 and finally he will be satisfied with the validity of the statement Anna.

Why ?

Because, if Anna is indeed having an affair, it is unlikely he could have found a unique solution to give the cipher for all options of Carl. If Carl just chose one option, it is likely to get away with cheating is Anna 27/28. BUT if Carl chose to do random tests several times, for instance he chose to test it as much as 150 times, a choice Anna to get away with cheating is down to (27/28) ^ 150 i.e. 0.5% <.

So, let's examine the property of zero knowledge of this scenario:

Completeness: the Program password used has been verified, to be honest, and Anna and Carl to follow Protocol.
Sound: If Carl Nonrandom perform tests as many as 150 times, possibly Anna get away with cheating is 0.5% <.
Zero-Knowledge: Anna never revealed on Carl what original solutions.

Proof vs Proof Of Statements

Now we know the theoretical aspects of the zero-knowledge proof and its application in a variety of examples of the practical application, what is in blockchain? Why is everyone raving about Zcash because applying the ZKP (without evidence of knowledge) and why everyone is happy with the Ethereal do the same? Before we expand it, it is important to know one of the more important theoretical concept.

What exactly are we prove it by using the ZKP? In a broad spectrum, there are two statements that you can prove using the ZKP. Proof a.k.a. facts and evidence knowledge.

-Proofs : This is the intrinsic truth of the universe you might want to prove through the ZKP. For example. "Number X belongs to the Group of Y".

-Proof of knowledge : You may also want to prove that you have knowledge about certain ideas without revealing what that particular knowledge. As can be seen in the example Sudoku cave, Waldo and Alibaba given above.

It is important to note the difference between the two because both are very different. In the world of crypto-cardiac, we mostly focus on "proof of knowledge". One of the most important breakthroughs in proving the evidence of knowledge through a zero knowledge proof appears when Claus-Peter Schnorr in 1980-an identification Protocol generates Schnorr. This Protocol laid the foundations of modern cryptographic signature key and showing how Zero-knowledge can be integrated seamlessly into modern cryptographic practice.

The Schnorr Identification Protocol

To understand what Schnorr's identification of Let's restore our old friend Anna and Carl. Anna has announced to the world that he has a public key and can accept and receive information through it. Carl, who has always been skeptical, arguing that Anna is lying. The only way for Anna could prove their honesty is by showing his personal key to Carl, but she doesn't want to reveal his private key.

So how does Anna reveals his knowledge of the private key without express it? This is where incoming Schnorr Protocol. Before we begin to understand how the protocol works, there are some parameters you need to know:

-p = Any prime number.
-q= factor of p-1.
-“a” such that a^q = 1 mod p.

To remember, in third, Schnorr Protocol this variable is global. This means that there are people who know about a third of these variables for specific scenarios.

Now we come to the two keys, a private secret key which we will call the "s" and the public key which we will call the "v".

s can be worth how over 0 < s < q.

v = a ^-s mod q.

Public key "v" will be a global knowledge and public together with p, q and a. However, only Anna knows what it is, because it is the private key.

So, now that we defined from, let's see how the exchange of information and the validity of the statement Anna can work without him reveal what the key privatnya.

Anna signed and send encrypted messages

Suppose that Anna would like to send the message "M" to the Carl who encoded with his private key. How he will do it if he followed Protocol Schnorr?

First, he will choose a random number "r" so that 0 < r < q.

Now he will compute the value x such that:

X = a ^ r mod thing.

Now after he counts the value of X, he will combine this with the original message. What is a Series? Suppose we have two strings "Hello" and "world". If we combine both, then we will get a "Hello World". The merger basically means add two strings and make it into one.

So, he will combine M and X to get M || X. and she will store a hash of this value in the e.

Basically, e = H (M || X) where H is a hash function.

Finally, when all this is done, he will do one last calculation. He will get a value of "y" in such a way that:

Y = (r + s * e) mod q

Now that all the computations are over, she is going to send the following pieces of information to Carl:

The massege "M"
The signatures e and y.

Carl receives the message and verify the proof of knowledge of Anna
Now Carl has received the following information: a message from Anna (M) and a signature (e and y).

Along with that, he has the following information that is known to the public for everyone:

-Anna public key "v".
-Main number Anna choose "p".
-"Q" which is a factor of "p-1" selected Anna.
-And "a" such that a ^ q = 1 mod p, also selected Anna.

Now, Carl will have to compute X’ such that:

X’ = a^y * v^e mod p

How to make zero knowledge proofs non-interactive?

With zero-knowledge verification system before, there is one big problem. For it to work, the comparison and the verifier must be online at the same time. In other words, the process is "interactive". This makes the whole system inefficient and virtually impossible. The measuring is not possible online at once as a comparison all the time? There needs to be a system to make it more efficient.

In 1986, Fiat and Shamir found heuristics Fiat-Shamir and managed to turn the zero knowledge interactive proof be proof zero knowledge that are not interactive. This helps the entire protocol works without any interaction. The procedure behind it is very simple.

So, for example, this is how zero knowledge proofs used to work before Fiat and Shamir.

What is the use of Zk-Snarks?

ZK-Snarks stands for "Zero-Knowledge Interactive Arguments concise Non-knowledge". Its use in modern blockchain technology is really great. To understand its application, it is important to know how the smart contract work. Smart contract is essentially an escrow fund that will be activated once a particular function is completed.

For example. Anna put 100 ETH in the contract that he got smart with Carl. Carl had to do certain tasks, completion, Carl will get 100 ETH of smart contracts.

This becomes complicated when the task should be Carl do are layers and secrets. Suppose you're entering into a contract with intelligent Anna. Now, you will only get the payment if you do A, B and c. What if you do not want to reveal details of A, B, and C because the secret of your company and you do not want any competition. to find out what you should do?

What does Zk-Snarks is that it proves that these steps have been taken in smart contracts without disclosing what exactly these steps. This is very useful is protecting the privacy of you and your company. It can only reveal part of the process without showing the entire process itself and prove that you are honest about your claim.

How do ZkSnarks work?

A Zk-Snark consists of three algorithms: G, P and V.

G is a generator of keys that take input "lambda" (which should be kept confidential and may not be disclosed in any condition) and a program c. then proceeded to generate two keys that are available to the public, a pk key, and verify Key vk. The key is public and available to the parties concerned.

P is a comparison which would use 3 items as input. The authentication key pk, random input x, which are available to the public, and a personal statement that they wanted to prove the knowledge without disclosing what it really was. Let's call a personal statement "w". The algorithm produces a proof of P such that: prf prf = P (pk, x, w).

Algorithm verifier V basically return boolean variables. Boolean variable has only two options, it could be TRUE or FALSE. So, the verifier take on key verification, public input x and evidence such as the prf as input:

V (vk, x, prf)

.. and return TRUE if the comparison is true and false.

Well, about the parameters of the lambda. The value of the "Lambda" should be kept confidential because anyone can use it to produce false evidence. Proof of this would be false returns TRUE regardless of whether the comparison actually has knowledge of a personal statement "w" or not.

The use of ZkSnarks in cryptocurrency

Image Courtesy: Zcash

Zcash is a crypto launched by Zerocoin Electic Coin Company on 9 September 2016 and is the first example of a crypto who married the concept of blockchain with ZkSnarks technology. It aims to provide a space that transactions are completely safe and protected for its users without disclosing details (such as their address) to anyone.

Ethereal want to integrate ZkSnarks when entering the phase of Metropolis and the way they planned it is by creating alliances with Zcash which includes the exchange of shared values. Head developer Zcash, Zooko Wilcox, giving a presentation at DevCon2 in Shanghai that explores the future of such an Alliance. According to him, there are 3 ways to order for Z-Cash and by extension, zk-snarks can be integrated with the Ethereum.

The first method is called the Baby Zoe (Zoe = Zcash on Ethereal). This adds a compiler pre-zk-snark about Ethereal and make smart contract Zcash mini in Ethereal. The idea is to see whether the system can create a DAPP Ethereal zk-snark over his blockchain.

The second method is to integrate kompensabilitas blockchain in Zcash Ethereum. As Wilcox put it, Ethereum greatest asset is its ability and people want to see if they can integrate it into the block zk-snark like Zcash. Can people create DAPPS in block made without proof of knowledge? It is something that they are waiting to see.

The third and most interesting aspect is Project Alchemy. This is basically a connection and interoperator of two blockchains in such a way so that one can move seamlessly between the two. How are Zcash plan to do it is to clone the Relay of BTC. This is a script written to make the Ethereum client lightweight Bitcoin in Ethereum. Cloning Zcash will use the same concept to create the light clients in Zcash Ethereum.

If this is successful, we will have the first decentralized currency system in the world to facilitate the creation of DAPPS without knowledge embedded in it.

Looking Ahead

There is no doubt that the introduction of a zero-knowledge proof will be a huge game changer to Ethereum. In a world that is increasingly open, connected and monitored, any privacy was well received. How integration happens remains to be seen, but runs with a theoretical concept itself, one cannot not passionate.

Give your opinions and suggestions in the comments of this post in order to better