Article de Huobi Quant Academy traduit par Azor Group

Résumé
La théorie des portefeuilles modernes est l'une des théories économiques les plus importantes et les plus influentes en matière de finance et d'investissement. La théorie fournit un cadre mathématique pour construire un portefeuille d'actifs qui maximise le rendement attendu pour un niveau donné de risque pris. Cet article applique la théorie au trading de crypto-monnaie et évalue son efficacité en matière de diversification des risques et d'amélioration du rendement des investissements.
Rapport complet
Nous avons construit des modèles mathématiques pour analyser l'efficacité de la diversification des risques de la théorie des portefeuilles modernes en utilisant les données historiques des 10 principales cryptomonnaies (BTC, ETH, XRP, BCH, EOS, LTC, ADA, XLM, TRX, IOTA). Le résultat a démontré qu'une diversification de portefeuille bien proportionnée au sein de Cryptocurrency Investment peut en effet réduire efficacement le risque idiosyncratique.
Préparation des données
.png)
Nous avons utilisé les données historiques de transaction des 10 principales crypto-monnaies (par capitalisation boursière) capturées par Coinmarketcap du 30 novembre 2017 au 21 mai 2018.
Traitement de l'information
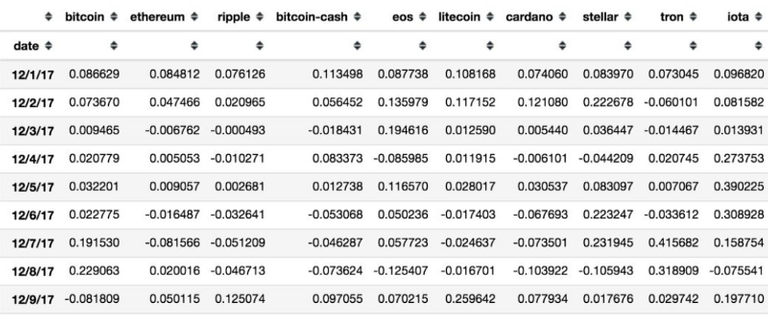
ROI quotidien des 10 principales crypto-monnaies
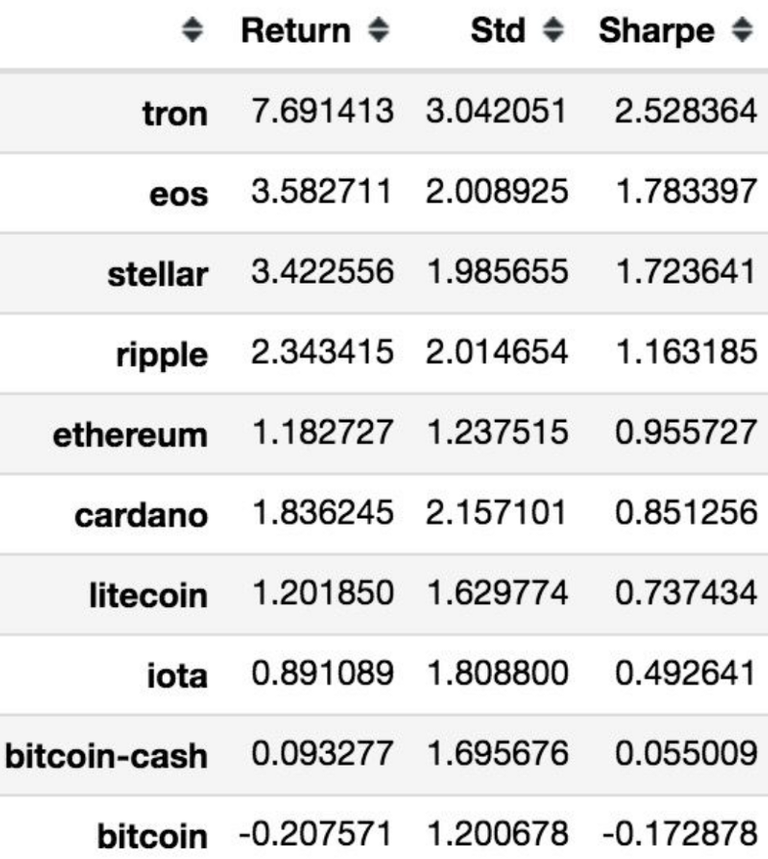
Écart type du ROI quotidien et du ratio de Sharpe des 10 principales crypto-monnaies
.png)
Matrice de covariance entre le prix des 10 plus grandes devises
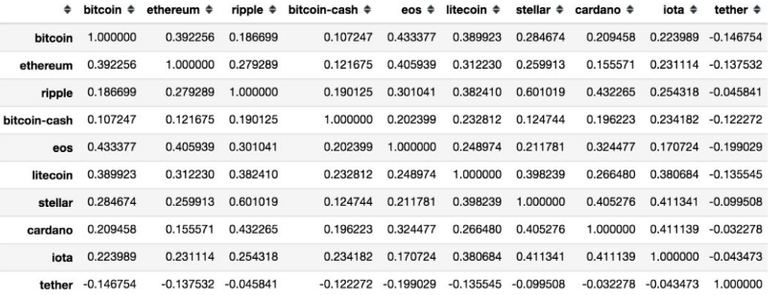
Pearson Correlation Matrix entre le prix des 10 principales crypto-monnaies
Modélisation mathématique
Nous avons construit le portefeuille sur la base de la théorie des portefeuilles modernes et attribué à chacune des 10 principales crypto-monnaie une pondération différente, avec un poids total de 1 au maximum. Nous pourrons ainsi obtenir des rendements plus élevés pour un niveau de risque donné. Ici, nous avons utilisé l'écart type du rendement quotidien pour évaluer le risque et utilisé le ratio de Sharpe pour évaluer l'efficacité de la diversification du portefeuille. Selon la théorie du portefeuille moderne, l'ajout d'actifs à un portefeuille diversifié présentant des corrélations inférieures à 1 peut réduire le risque du portefeuille sans sacrifier le rendement. Une telle diversification permettra d’augmenter le ratio de Sharpe d’un portefeuille.
Ratio de Sharpe = (rendement attendu du portefeuille - taux sans risque) / écart type du rendement du portefeuille
Sous deux conditions (tous les poids sont supérieurs à 0 et tous les poids totalisent 1), nous avons construit un modèle stochastique en calculant respectivement l'écart type du rendement du portefeuille, le rendement attendu du portefeuille et le ratio de sharpe sur 500 000 valeurs aléatoires. En conséquence, nous avons pu trouver un ensemble de portefeuilles de placement optimaux.
Résultats
Vous trouverez ci-dessous le diagramme de dispersion créé à partir de 500 000 simulations stochastiques, l'axe des abscisses représentant la volatilité attendue (écart type du rendement du portefeuille) et l'axe des y représentant le rendement attendu du portefeuille. La taille du ratio de sharpe est représentée par différentes couleurs des points, avec une couleur plus profonde représentant un plus grand ratio de sharpe. À partir de l'intrigue, nous pouvons voir que les points proches du coin inférieur droit du graphique ont des ratios de sharpe plus importants qui représentent une meilleure diversification du portefeuille. Les points dans le coin supérieur gauche sont délimités par «frontière efficace» - un ensemble de portefeuilles optimaux offrant le rendement attendu le plus élevé pour un niveau ou un risque défini ou le risque le plus faible pour un niveau de rendement attendu donné.
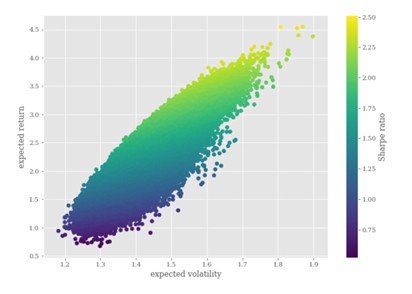
Nous pouvons alors tracer la limite efficace et trouver le meilleur portefeuille avec le plus grand ratio de sharpe, marqué par l’étoile rouge dans la figure ci-dessous.
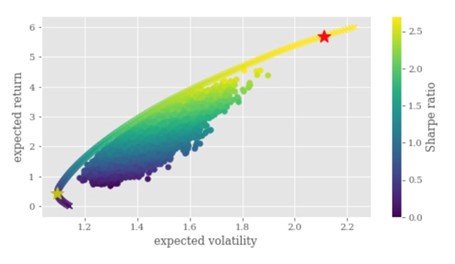
Nous pouvons alors connecter l'étoile rouge à l'origine (puisque nous supposons que le retour sans risque est égal à 0) et tracer la ligne du marché des capitaux - le meilleur portefeuille composé d'actifs sans risque et à risque le long de la ligne efficace.
.png)
Nous avons ensuite tracé les limites efficaces, les rendements attendus du portefeuille optimal et de la monnaie unique, les écarts-types sur le même graphique afin de comparer la diversification des risques.
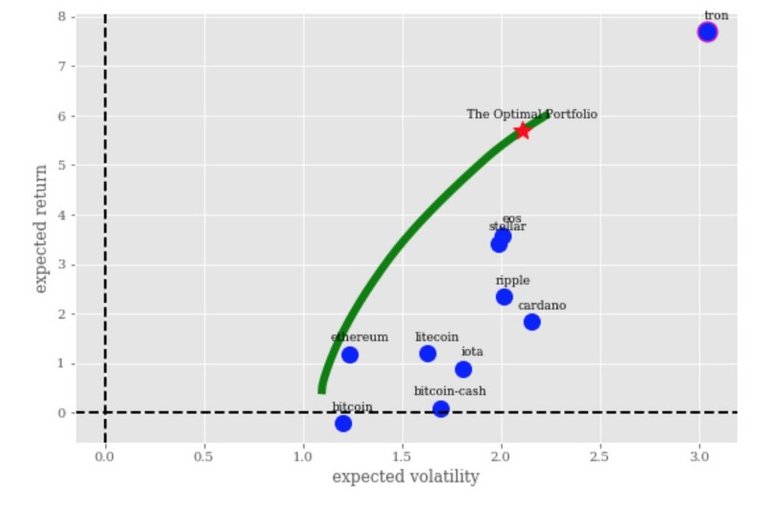
Conclusion
Sur la base de l'évaluation ci-dessus, nous pouvons voir qu'il est effectivement possible d'utiliser la théorie du portefeuille moderne pour construire une frontière efficace de portefeuilles optimaux offrant le rendement attendu maximum possible pour un niveau de risque donné. Cependant, nous réalisons qu'il existe de nombreuses autres théories et modèles financiers à étudier, et nous continuerons d'explorer ces théories et modèles dans nos prochains rapports.
Les références
- Zvi Bodie, 10ème édition d'Investissements;
- Jonathan Berk, Peter DeMarzo, 3e édition de Corporate Finance;
- Harry Markowitz, sélection de portefeuille;
- Wes McKinney, Python pour l'analyse des données
Viens faire un tour sur notre communauté Telegram!
Tu y retrouveras tout ce dont tu as besoin pour la crypto : des reviews d'ICO, notre spreadsheet, des articles de tout niveau, du trading et les dernières informations!
🙏 |Si tu aimes cet article, n'hésite pas à upvoter / commenter / resteemer
🙌 | Si tu aimes notre travail et que tu veux nous soutenir en nous faisant un don en ETH, c'est par ici : 0x27D31fa37FA5dC2B19134302517e27342b649F2a


