1918년 이전
다윈주의와 멘델주의 사이의 논쟁이 끊이지 않았던 것은 기본적으로 사람의 키와 같이 '연속적으로 분포하는' 형질과 콩의 색깔 같이 '불연속적으로 분포하는' 형질을 동시에 설명할 수 있는 유전모델의 부재 때문이었습니다. 고정불변하는 한 쌍의 대립 유전자에 의해 형질이 결정되는 멘델의 가정이 옳다면 키와 같은 연속적인 형질은 생길 수가 없었습니다. 기껏해야 AA, Aa, aa 만이 가능할 뿐입니다. 뿐만 아니라 두 부모 사이에서 태어난 자손의 키 분포도 소위 3:1를 따라야할텐데 실제로는 그렇지 않다는 게 문제였습니다(Galton, 1886).
골턴은 Law of Ancestral Heredity라는 일종의 혼합유전이론을 통해 키와 같은 연속적 형질을 설명하고자 했습니다. 그러나 혼합유전은 멘델주의자들의 반복된 실험을 통해 여러 번 반박된 이론이었습니다. 아니 정확히 말하면, 키와 같은 연속형질은 잘 설명하지만 콩의 색깔같은 불연속적인 형질은 설명하지 못했던 것입니다.
그렇다고 이 둘을 조화시키고자 하는 시도가 아예 없었던 것은 아닙니다. Bateson(1901), Yule(1902)는 멘델주의와 다윈주의 양쪽의 의견을 검토하여 멘델주의를 받아들이면서도 연속형질을 설명할 수 있는 방법을 발견합니다. 그림 1.은 Yule의 1902년 논문으로 복수의 유전자가 하나의 형질에 관여한다고 가정하면 멘델주의의 관점에서 연속형질을 설명할 수 있다고 주장합니다.

그림 1. Mendel's Laws and Their Probable Relations to Intra-Racial Heredity (Yule, 1902)의 한 부분
단락의 마지막 문장, '(전략) or may be due to the compounding in some way of the discontinuous variations of a number of such elements.', 에서 Yule은 요즘 말로 다인자(polygenic) 유전이 연속형질을 설명할 수도 있다는 가설을 제시하고 있습니다. 그러나 이 논문은 다인자 유전만을 다루는 연구도 아니었으며 다인자 유전을 언급하는 단락도 딱 저기 뿐이었습니다. 뿐만 아니라 당시 두 집단 간의 갈등이 극도로 격화된 상황에서 이러한 '화해의 시도'는 모두 잊혀졌죠. 완벽한(?) 다인자 유전이론의 등장은 결국 20년 뒤로 미뤄지고 맙니다.
그리고 1918년
두 집단의 싸움이 끊이질 않던 시기, 로널드 피셔(R. A. Fisher)라는 28세의 박사과정생이 The Correlation between Relatives on the Supposition of Mendelian Inheritance (1918)라는 제목의 연구를 발표합니다. 이는 다인자 유전을 수학적 방법론을 통해 체계적으로 분석한 최초의 연구였습니다. 그는 Bateson과 Yule 등이 이전에 제시한 (그의 표현을 빌리자면) cumulative Mendelian factors를 받아들이면 기존 멘델주의 연구 뿐만 아니라 Galton 등 다윈주의자들이 제시한 결과들까지 모두 자연스럽게 포괄할 수 있음을 입증합니다.

그림 2. The Correlation between Relatives on the Supposition of Mendelian Inheritance (1918)의 마지막 절 중 일부
그렇다면 이 Polygenic Model(다인자 유전 모델, 여러 이유로 앞으로 영어로 쓰겠습니다)이 어떻게 연속형질을 설명하는지 알아보도록 합시다.
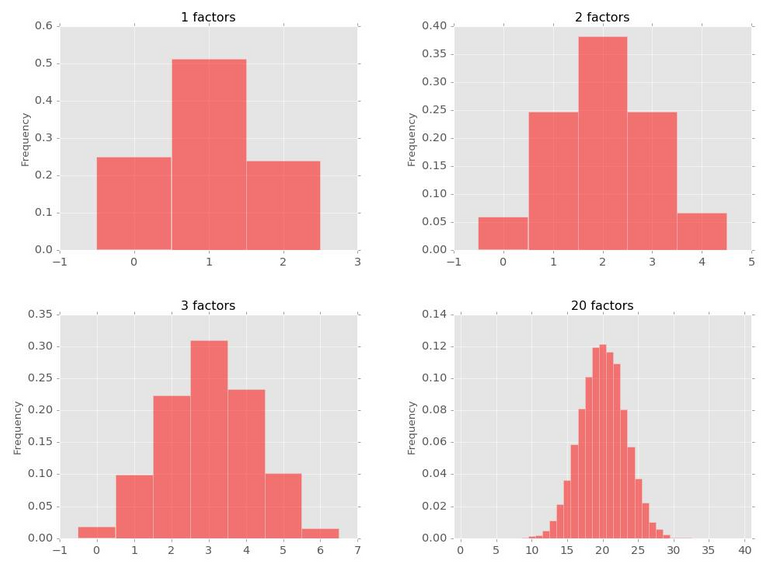
그림 3. 순서대로 1개, 2개, 3개 및 20개의 유전자 좌위에 의해 결정되는 형질의 분포
위 그림에 주목해주세요. 우성성(Dominance)를 무시하면 하나의 유전자에 의해 결정되는 형질은 세 가지 값을 가질 것입니다. 유전자형이 AA, Aa, aa 세 가지 밖에 없으니까요(좌측상단). 그런데 두 개의 유전자에 의해 결정되는 형질은 어떨까요? 문제를 단순화하기 위해 이 형질은 해당 개체가 가지고 있는 대문자 대립유전자의 갯수에 비례한다고 가정합시다. 예를 들어, 유전자 1의 유전자형이 Aa, 유전자 2의 유전자형이 Bb 인 사람의 형질값은 2, 각각 AA BB인 사람의 형질값은 4라고 하자구요. 그러면 가능한 대문자의 갯수는 0부터 4까지 존재하므로 총 5개의 값이 가능해집니다(우측상단). 유전자 3개가 이 형질을 결정하는 경우에는 가질 수 있는 대문자 대립유전자의 갯수가 0(aabbc) ~ 6(AABBCC) 이므로 총 7개의 값이 가능해집니다(좌측하단). 이 갯수를 점점 늘려서 20개의 유전자에 의해 결정되는 형질은 0 ~ 20으로 총 21가지 값을 가질 수 있습니다.
그리고 이 그래프들의 모양을 유심히 관찰하면 해당 형질에 관여하는 유전자의 갯수가 많아질수록 점점 더 연속적인 정규분포에 가까워진다는 것을 관찰할 수 있습니다. 알려져 있다시피 우리의 키도 이러한 연속적인 정규분포를 보여주므로 피셔는 키의 분포가 본인의 Polygenic Model로 설명될 수 있다고 주장합니다. 참고로 다소 수학적인 얘기인데, 실제로 이 분포가 정규분포로 수렴한다는 것은 수학적으로 증명할 수 있습니다(Central Limit Theorem).
그리고 피셔의 발견으로부터 100년이 흐른 지금, 현대 유전학은 생물이 가지고 있는 대부분의 형질들이 Polygenic 하다는 것을 알아냈습니다. 그렇기 때문에 질병 연구든 진화 생물학 연구든 통계학 없이는 불가능한 것입니다. 그래서 안타깝게도 이후의 글들에서는 다소 어렵더라도 통계학 얘기를 안 할 수가 없을 것 같네요. 사실 100년이 지난 지금도 우리가 가지고 있는 도구들은 피셔 시대의 그것보다 특별히 더 나아진 것이 없습니다. 하디-베인베르크 법칙, Polygenic model of quantitative traits 등등 ... 이 시대 유전학자들은 대체 뭘 먹고 공부했길래 이런 생각을 했던 것인지 참 궁금하기도 하고 부럽기도 하고 그렇네요.
윽 중심극한정리....머리가.......