Im letzten Artikel bin ich von einem einfachen Causal Loop Diagram ausgegangen, das die Anzahl Hühner und die Anzahl Eier einer Hühnerfarm in einem Kreis darstellte und habe daraus einen ersten Draft eines System Dynamics Modell entwickelt. Zum Schluss habe ich festegestellt, dass die beiden Bestände eigentlich nicht unabhängig voneinander sind. Vielmehr "fliessen" die Eier in die Hühner in dem Sinne, dass jedesmal, wenn esich der Hühnerbestand um Eins erhöht, der Eierbestand um Eins zurück geht.
Nutzung
Im folgenden Modell habe ich versucht, diese Beobachtung zu berücksichtigen. Ich möchte das Modell hier näher beschreiben:
Das Modell Huhn Ei verbessert kann direkt geöffnet und kopiert werden. Folgen Sie dem Link!
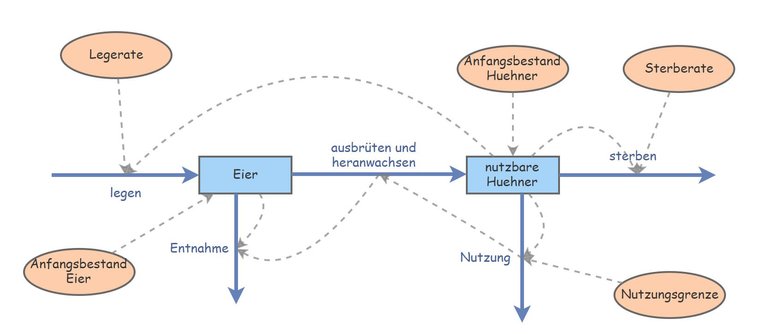
Wir starten unsere Farm mit einem Anfangsbestand an Hühnern, hier z.B. 1800 Stück. Jedes legt pro Tag ein Ei, d.h. ab dem zweiten Tag haben wir ungefähr soviele Eier, wie Hühner. Mit dem Parameter "Legerate" können wir einstellen, wieviele Eier pro Tag eines unserer Hühner legt. An einigen Tagen legen sie zwei Eier, manchmal keines, etc. Die Legerate ist eine Durchschnittsgrösse und wird vermutlich etwas höher als 1 sein. Das muss die Hühnerfarm durch Messungen feststellen.
Wir nutzen unsere Hühner, indem wir täglich die schönsten Exemplare an Hühnerliebhaber verkaufen, die sie in Schönheitswettbewerben ausstellen (es soll auch Farmen geben, die die Hühner schlachten; aber unsere ist keine solche). Die Nutzungsrate kommt dadurch zustande, dass sie von der Differenz zwischen dem aktuellen Hühnerbestand und einer Nutzungsschwelle abhängt. Die Nutzungsschwelle gibt den Hühnerbestand an, den wir niemals unterschreiten wollen, denn wir wollen ja auch täglich genug Eier verkaufen. Ich habe hier die Nutzungsschwelle auf 1000 eingestellt.
Ausbrüten von Eiern als Kompensation der Nutzung
Die Nutzungsrate errechne ich durch (Hühnerbestand-Nutzungsschwelle)*0.02, d.h. ich verkaufe täglich zwei Prozent derjeniger Hühner, die die Nutzungsschwelle überschreiten. Die relative Nutzungsrate von zwei Prozent könnte ich auch noch als Parameter modellieren. Ich habe sie hier jedoch fest einprogrammiert, um das Modell nicht zu überladen.
Um die Nutzungsentnahme zu kompensieren, lasse ich immer gleich viele Eier ausbrüten, wie ich Hühner verkaufe. Allerdings kommen die geschlüpften Hühner frühestens am Ende der 21tägigen Brutzeit zum Bestand der Hühner. Da frisch geschlüpfte Kücken noch an keinen Schönheitswettbewerben teilnehmen dürfen, muss ich ihnen noch ein paar Tage Kindheit gönnen. Ich habe hier 100 Tage zu der Brutzeit gerechnet, d.h. wenn ich heute ein Ei ausbrüten lasse, dann erhöht sich mein Hünerbestand nach 121 Tagen um ein neues Huhn.
Hier würde man besser eine sogenannte "Aging Chain" einbauen: Die geschlüpften Kücken kommen zuerst in einen Bestand "Kücken" und "fliessen" erst nach 100 Tagen in den Bestand nutzbarer Hühner. Dadurch könnte man auch die unterschiedlichen Verzögerungsqualitäten zwischen Brüten und Heranwachsen modellieren.
Verzögerungen sind ein grundsätzliches Element in System Dynamics Modellen. Hier wurde eine sogenannte pipeline material flow delay angewendet. Ich werde gelegentlich etwas über die verschiedenen Verzögerungen schreiben, die in System Dynamics zum Einsatz kommen. Vorläufig verweise ich auf den Artikel Delays, Smoothing and Averaging
Eierentnahme
Nun kommt die Überlegung, dass die brütenden Hühner als Legehennen wegfallen und sich das Brüten negativ auf den Eierbestand auswirkt. Das müsste man in der Tat modellieren, wenn die Eier tatsächlich von den Hühnern ausgebrütet werden. Legehennen haben aber verlernt zu brüten, und in Hühnerfamen werden die Eier künstlich im Brutkasten ausgebrütet. Welche Vereinfachung unseres Modells!
Die Eierentnahme orientiert sich nun an der Anzahl Eier, die ausgebrütet werden. Wir können einfach den Rest der Eier entnehmen, d.h. Entnahme = Eierbestand - in Brut befindliche Eier. Da ich die Reifezeit ebenfalls in die Brutzeit mit eingerechnet habe, habe ich hier einen kleinen Fehler, den ich in einer Weiterentwicklung korrigieren kann. System Dynamics Modelle werden am Besten rekursiv entwickelt, indem man die Modellversionen immer ausgereifter und umfangreicher macht. Es ist so eine Art agile Softwareentwicklung.
Schliesslich habe ich mit einem Abfluss aus dem Bestand der Hühner eine Mortalität modelliert. Gewöhnlich bleiben die Hühner nicht bis zu ihrem natürlichen Tod in der Farm. Jedoch möchte ich die Auswirkung von Krankheitsrisiken und Epidemien studieren. Bevor ich das tue, simuliere ich das bisherige Modell über 365 Tagen:
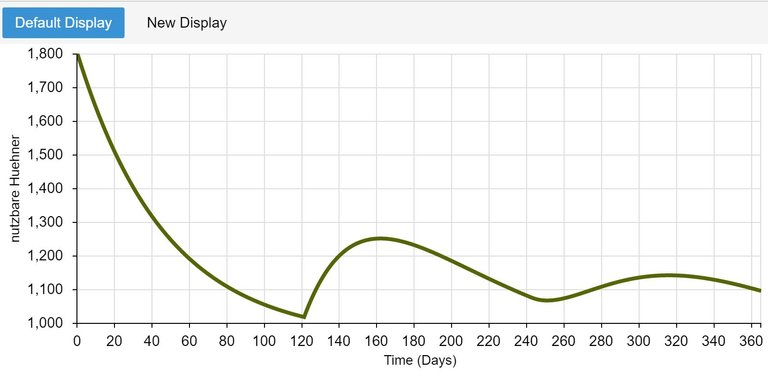
Entwicklung des Hühnerbestandes über 365 Tagen
Wie man sieht, ist das Modell ganz offensichtlich nicht-linear.
Risikobewertung
Wie wir sehen, nähert sich der Hühnerbestand exponentiell der Nutzungsschwelle von 1000 Exemplaren. Nach 121 Tagen kommen die neu herangewachsenen Individuen hinzu, so dass sich der Bestand wieder etwas erholt. Das führt zu einer gedämpften Schwingung, die sich bei einem Bestand von ca. 1100 Tieren einpendeln wird.
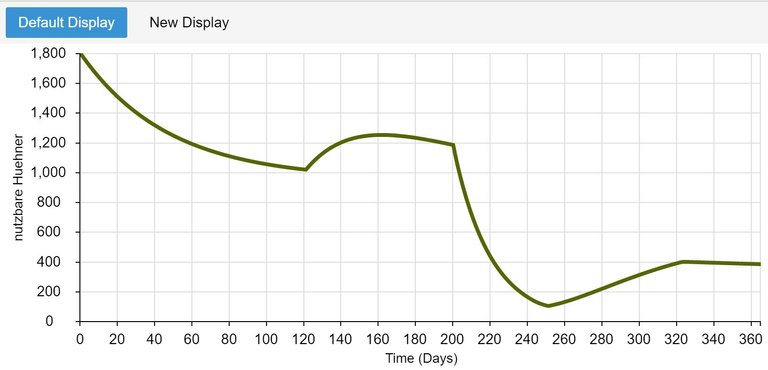
Entwicklung des Hühnerbestandes bei einer Epidemie
Nun bauen ich in der Sterberate mit einer PULSE-Funktion eine Krankheit ein, die am Tag 200 ausbricht und 50 Tage anhält. Die Auswirkung auf den Hühnerbestand ist fatal: der Bestand wird auf 400 Individuen herab sinken. Natürlich hängt das von der Schwere des Krankheitsverlaufs ab. Ich habe hier eine natürliche Mortalität von 0.001 pro Tag angenommen, d.h. dass wenn ich 1000 Hühner habe, täglich 1 Huhn stirbt. Das ist vermutlich zu viel. Die Krankheit modellierte ich dann so:
0.001+Pulse(200, 0.05, 50, -1)
Das bedeutet: auf der natürlichen Sterberate von 0.001 setzt ab dem Tag 200 eine Erhöhung um 0.05 ein. Diese hält 50 Tage lang an und wiederholt sich nicht. Zwischen dem Tag 200 und dem Tag 250 beträgt die Sterberate also 0.051, was täglich 51 toten Individuen entspricht.
Auf diese Weise lassen sich Risiken studieren. Zwar kennen wir weder die Mortalität, noch die Dauer, noch den Zeitpunkt des Ausbruchs einer Krankheit. Aber wir können uns auf solche Risiken vorbereiten, indem wir entsprechende Policies erlassen, wie z.B. die Höhe der Nutzungsschwelle.
In einer nächsten Folge, werde ich dieses Modell ausbauen und durch ökonomische Parameter ergänzen.
Würde noch hinzufügen, welche Tools du nutzt; für diejenigen, die sich auch mal ausprobieren wollen. Hier ist es: Insight Maker ( kostenlos online nutzbar, recht intuitiv, kann sogar nicht-lineare Funktionen).
Grüße
edit: Achso, hatte die Links nicht gesehen, die doch direkt auf die Seite von Insight Maker führen...
Meine Links führen nicht nur zu Insightmaker, sondern direkt zum Modell. Alle, die dort landen, können das Modell kopieren und zu eigenen Zwecken verändern oder weiter entwickeln. Sie können ihre Änderungen hier bekannt geben, so dass alle anderen wieder auf das veränderte Modell zugreifen und daran weiter arbeiten können.
Der Insightmaker unterstützt hochgradig kollaboratives Arbeiten! Das macht Spass!