Die Unendlichkeit und noch viel weiter - Teil 3

in #de-stem • 7 years ago


motorhead_purple.png
Bild Quelle

Roadmap

"Die Unendlichkeit und noch viel weiter" ist eine Reihe von Artikeln, über die mathematischen Eigenschaften von Unendlichkeit und wie unsere Intuition über die Unendlichkeit häufig daneben liegen kann. In den späteren Teilen wird es recht mathematisch und wir werden nicht um ein paar Formeln herum kommen. Ich werde jedoch mein bestes geben die Artikel so verständlich wie möglich zu schreiben. Sie müssen nicht Mathematik studiert haben, um sie zu verstehen.

Dies sind die bereits geplanten Teile der Artikelreihe. Es kann sein, dass diese Liste noch überarbeitet wird.

Gibt es größeres als unendlich?

Im letzten Teil dieser Serie haben wir festgestellt, dass die Größe einer unendlichen Menge nicht durch Hinzufügen von endlich vielen Elementen verändert wird. Wir haben eine Methode kennengelernt, mit der wir die Gleichheit der Größe zweier Mengen zeigen können und haben etwas mit den natürlichen Zahlen gespielt. Aber können wir etwas größeres finden?

Ja, es gibt Mengen, die größer sind als die Menge der natürlichen Zahlen obwohl die natürlichen Zahlen bereits unendlich groß sind. Bisher haben wir gezeigt, dass zwei Mengen dieselbe Größe haben, indem wir eine Bijektion gefunden haben. Die Ungleichheit zweier Mengen zu beweisen ist jedoch nicht so einfach. Hierfür müssten wir nämlich zeigen, dass es keine Bijektion geben kann. Das ist jedoch nicht so leicht, da es mindestens so viele Funktionen gibt, wie es natürliche Zahlen gibt, also unendlich viele. Zu zeigen, dass alle diese Funktionen nicht bijektiv sind ist nicht möglich für Menschen mit endlicher Lebensdauer. Bevor wir uns also dem Beweis der Ungleichheit widmen, bleiben wir noch ein klein wenig länger bei der Größe der natürlichen Zahlen.

Wo wir schon mal dabei sind, geben wir der Größe der natürlichen Zahlen doch einen Namen. Wir verwenden die natürlichen Zahlen zum Zählen... Der Name "abzählbar unendlich" klingt doch gar nicht schlecht. (Ich habe mir den Namen natürlich nicht ausgedacht. Es ist der offizielle mathematische Begriff dafür.)

Die Menge aller rationalen Zahlen

Schauen wir uns die Menge der rationalen Zahlen an, also die Menge aller Brüche mit ganzzahligen Zählern (die Zahl über dem Bruchstrich) und natürlichen Nennern (die Zahl unter dem Bruchstrich). Wenn man die ganzen Zahlen nimmt und sie alle nacheinander durch alle natürlichen Zahlen teilt, bekommt man die rationalen Zahlen.


01.png
(Wir erinnern uns: Die Null ist keine natürliche Zahl.)

Die Menge aller rationalen Zahlen ist genauso groß wie die Menge aller natürlichen Zahlen, sie ist abzählbar. Sich das vorzustellen ist sicherlich etwas schwieriger als beim Hinzufügen eines Elements. Und ja, hierfür eine Bijektion zu finden ist durchaus etwas schwieriger. An dieser Stelle empfiehlt es sich kurz einen Moment zu überlegen, wie diese Bijektion aussehen könnte.


question-mark-2123969_640.jpg
Bild Quelle

Eine bijektive Funktion hierfür mathematisch-formell zu definieren ist recht schwer und umständlich, also versuchen wir etwas anderes. Bisher haben wir immer den allgemeinen Fall untersucht, wo wir zwei beliebige Mengen verglichen haben. Dieses mal jedoch wollen wir nur wissen, ob diese Menge gleichgroß wie die Menge der natürlichen Zahlen ist, also ob sie abzählbar ist.

Wenn wir einen Weg finden können, um alle Elemente zu zählen, ohne je eins auszulassen, dann haben wir praktisch eine surjektive Abbildung von den natürlichen Zahlen in die Zielmenge gefunden (die Definition einer surjektiven Abbildung ist, dass alle Elemente der Zielmenge erreicht werden). Wir müssen nur sicherstellen, dass wir kein Element auslassen.

Wenn Sie den vorherigen Teil dieser Serie gelesen haben, dann kann es sein, dass Sie sich jetzt fragen "Moment... Benötigen wir nicht eine Bijektion, also eine Funktion die sowohl surjektiv als auch injektiv ist!?". Ja, das gilt wenn wir beliebige Mengen vergleichen wollen. Uns interessiert aber nur, ob die Menge abzählbar ist, also ob sie höchstens so groß ist wie die natürlichen Zahlen. Eine Surjektion ermöglicht genau dies. Mit einer Bijektion lässt sich Gleichheit zeigen, mit einer Surjektion lässt sich zeigen, dass das Ziel höchstens so groß ist wie die ursprüngliche Menge.

Surjektiv bedeutet [...], dass alle Elemente der Ausgabemenge erreicht werden können indem man ein Element der Eingabemenge in die Funktion gibt. Anders formuliert, es existiert kein Element in der Ausgabemenge, welches nicht durch die Funktion und die Eingabemenge erzeugt werden kann.

Zitiert aus Teil 2.

Zum Glück ist abzählbar unendlich die kleinste Unendlichkeit (unter der Annahme, das Auswahlaxiom gilt; genauer gehen wir hier darauf nicht ein). Eine surjektive Abbildung von den natürlichen Zahlen auf unsere Zielmenge ist also ausreichend um Abzählbarkeit und in diesem Fall sogar Gleichheit zu zeigen. Wieso ist die Menge aller natürlichen Zahlen die kleinste unendliche Menge? Naja, wenn man eine beliebige unendliche Teilmenge wählt, so kann man immer eine Bijektion auf die natürlichen Zahlen finden. Jede unendliche Teilmenge der natürlichen Zahlen ist also gleichgroß wie die natürlichen Zahlen selbst und damit muss die Menge der natürlichen Zahlen die kleinste unendliche Menge sein.

Es ist also ausreichen einen Weg zu finden, die rationalen Zahlen zu zählen. Wir müssen uns keine Gedanken machen, zahlen doppelt zu zählen, wir müssen nur aufpassen, dass wir auch wirklich alle Zahlen zählen. Erinnern wir uns an die definition der rationalen Zahlen "alle Zahlen a geteilt durch b mit allen ganzen Zahlen a und allen natürlichen Zahlen b". Überlegen wir erst einmal wie wir alle rationalen Zahlen aufschreiben können. Wir nehmen eine Tabelle und schreiben alle ganzen Zahlen in die erste Zeile und an den Anfang jeder folgenden Zeile schreiben wir alle natürlichen Zahlen. In den inneren Feldern schreiben wir jetzt alle rationalen Zahlen a/b (a geteilt durch b) auf mit a aus den Spaltenüberschriften und b aus den Zeilenanfängen.

0-11-22-33⋯
10/1-1/11/1-2/12/1-3/13/1
20/2-1/21/2-2/22/2-3/23/2
30/3-1/31/3-2/32/3-3/33/3
40/4-1/41/4-2/42/4-3/43/4
50/5-1/51/5-2/52/5-3/53/5
⋮⋱

Wenn man diese Tabelle betrachtet und sich die definition der rationalen Zahlen in Erinnerung ruft, dann ist es recht einfach einzusehen, dass wir auf diese Art wirklich alle rationalen Zahlen aufgeschrieben haben. Jetzt müssen wir nur noch einen Weg finden diese zu zählen. Naja, wir können nicht Zeile für Zeile von Links nach Rechts vorgehen, die Zeilen sind schließlich unendlich lang, wir würden also nie die zweite Zeile erreichen. Spalte für Spalte? Selbes Problem, da auch jede Spalte unendlich lang ist.

Ich schnappe mir mal einen Stift und Zettel. (Ich lasse die Werte in der Tabelle weg, um zu vermeiden dass meine Hand abfällt.)


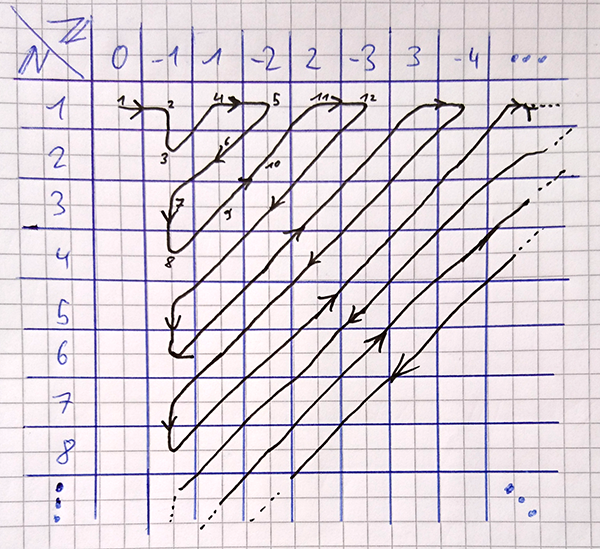
counting_rationals.png

Auf diese Art und Weise können wir alle rationalen Zahlen zählen. Da die Diagonalen von unten-links nach oben-rechts alle endlich sind, können wir diese problemlos eine nach der anderen zählen. Die erste Spalte ist größtenteils ausgelassen, weil sie nur Nullen enthält. Zahlen doppelt zu zählen ist zwar in Ordnung, aber wir müssen es ja nicht absichtlich tun.

Wir haben also einen Weg gefunden, die rationalen Zahlen zu zählen und haben damit gezeigt dass die rationalen Zahlen abzählbar unendlich sind.

Gib mir endlich was größeres!

Ich habe etwas größeres versprochen und ich werde liefern. Es war allerdings wichtig zu vermitteln, wie eine andere Art etwas zu schreiben manchmal zu einer einfachen Lösung führen kann. Da wir das jetzt hinter uns haben, schauen wir uns endlich etwas an was größer ist als die Menge der natürlichen Zahlen.

Trommelwirbel bitte.

Die reellen Zahlen! Die Menge der reellen Zahlen enthält alle rationalen Zahlen sowie alle irrationalen Zahlen. Irrationale Zahlen sind Zahlen, die nicht durch einen Bruch aus ganzen Zahlen dargestellt werden können. Dies führt zu unendlich langen, sich nicht wiederholenden Zahlen. Wie die Kreiszahl Pi. Hier sind die ersten 76 Ziffern der Zahl Pi:


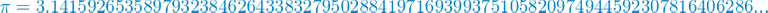
02.png

Das sind jedoch be weitem nicht alle Ziffern. Pi geht weiter und weiter und weiter, die Ziffern wiederholen sich nie und hören nie auf. Wenn Sie 1.000.000 Ziffern von Pi ausgedruckt auf einem eine Meile langen Stück Papier sehen wollen, dann schauen Sie sich doch mal dieses Video von Numberphile auf YouTube an. Wenn Sie meine Beiträge mögen, dann ist es wahrscheinlich dass sie auch die Videos von Numberphile mögen.(Leider sind diese jedoch nur auf Englisch.)

Selbst zwischen zwei beliebig dichten rationalen Zahlen finden sich unendlich viele weitere rationale Zahlen. Doch zwischen jeden zwei rationalen Zahlen, egal wie dicht diese beieinander sind, finden sich immer noch unendlich viele irrationale Zahlen. Wie Sie sehen können sind hier bereits mehrere Schichten von Unendlichkeit am Werk. Die reellen Zahlen sind so dicht gepackt, dass wir sie nicht mehr alle zählen können. Es ist unmöglich die reellen Zahlen zu zählen ohne eine auszulassen. Selbst mit unendlich viel Zeit ist es nicht möglich. Die reellen Zahlen sind "überabzählbar". Aber wie beweisen wir das?

Das Diagonalargument

Cantor's zweites Diagonalargument ist einer dieser Fälle bei dem die Lösung einfach wird, indem man das Problem anders aufschreibt.1 Um unser Leben etwas zu vereinfachen betrachten wir nur eine winzig kleine (im Vergleich zum Ganzen) Teilmenge der reellen Zahlen. Wir betrachten nur die Zahlen zwischen 0 (inklusive) und 1 (exklusive), die nur aus den Ziffern 0 und 1 bestehen. Zum Beispiel 0,011011101001 oder 0,100001 usw. Wenn wir zeigen können, dass diese kleine Teilmenge bereits überabzählbar ist, dann müssen auch die gesamten reellen Zahlen überabzählbar sein.

Zum Aufschreiben der Zahlen lassen wir die "0," am Anfang weg (die Zahl 0,0010101 wird also repräsentiert durch 0010101). Die Reihenfolge in der wir die Zahlen aufschreiben (also in der wir sie zählen) ist irrelevant, wir müssen nur bedenken dass jede Zahl unendlich lang ist. Unter Berücksichtigung dieser Kriterien fangen wir einfach mal an Zahlen aufzuschreiben. Schreiben wir eine Zahl in jede Zeile und davor immer den Index dieser Zahl, also die Reihenfolge der Zahlen.

index
10001001⋯
21100100⋯
31001011⋯
40111111⋯
51011100⋯
61000001⋯
71111111⋯
⋮⋱

Das sind Zahlen, ja. Aber sind das auch alle reellen Zahlen? Sprich, können wir so alle reellen Zahlen unserer kleinen Teilmenge aufschreiben? Hmmm, schauen wir uns einmal die Diagonale dieser Tabelle an. (Fett markiert)


03.png
(Zur Erinnerung, d repräsentier die Zahl 0,0101101... unendlich erweitert mit 0en und 1sen.)

Okay, das ist ebenfalls eine Zahl unserer Teilmenge. Schauen wir mal was passiert, wenn wir diese Zahl invertieren indem wir alle Ziffern 0 mit der Ziffer 1 und umgekehrt austauschen, nur so zum Spaß.


04.png

Oh oh. Da haben wir wohl ein Problem. Was haben wir gerade getan? Wir haben uns die Diagonale angeschaut. Dann die Diagonale invertiert. Diese Zahl jedoch ist auch eine Zahl aus unserer Teilmenge.

Alle Zeilen sind unendlich lang und alle Spalten sind unendlich lang. Das bedeutet, dass jede einzelne Zahl exakt eine Ziffer zu der Diagonalen beiträgt. Das bedeutet aber auch, dass jede Zahl die wir aufgeschrieben haben an mindestens einer Stelle von der invertierten Diagonale abweicht. Egal welche Zahlen wir aufschreiben und egal wie lange wir dies tun, wir werden niemals in der Lage sein die invertierte Diagonale in unserer Liste aufzuschreiben. Also fehlt mindestens eine Zahl der Teilmenge, wenn wir versuchen diese zu zählen.

Das Ergebnis: Die Menge der reellen Zahlen zwischen 0 und 1, die nur aus den Ziffern 0 und 1 bestehen überabzählbar. Entsprechend kann auch die Menge aller reellen Zahlen nicht abzählbar sein. Die Menge der reellen Zahlen ist also tatsächlich größer als die Menge der natürlichen Zahlen, obwohl beide unendlich sind.


staircase-917562_640.jpg
Bild Quelle

Nagut, den vorherigen Paragraphen müssen Sie vielleicht noch ein paar mal lesen. Versuchen Sie sich vorzustellen, was passieren würde wenn wir jetzt versuchen würden die invertierte Diagonale in die Liste einzufügen. Würden wir das tun, würde auch diese Zahl wieder mit einer Ziffer zu der Diagonalen beitragen und damit die Diagonale verändern. Dies würde wieder in einer anderen invertierten Diagonalen resultieren, die wieder in der Liste fehlt. Es handelt sich hier um ein unlösbares Paradoxon. Dieses Paradoxon existiert, weil die reellen Zahlen überabzählbar sind.

Sollten Sie es immer noch nicht verstanden haben, dann schrei(b)en Sie mich bitte in den Kommentaren an, weil ich so schlecht erklärt habe. Ich werde mein Bestes geben und so lange, erklären und umformulieren bis jeder einzelne meiner Leser diesen Beweis verstanden hat.

Wie groß können Mengen denn dann werden?

Wie groß hätten Sie es denn gerne? Es gibt unendlich viele Mächtigkeiten von Unendlichkeit, bzw. unendlich viele "Kardinalzahlen". Der deutsche Mathematiker Georg Ferdinand Ludwig Philipp Cantor (1845 - 1918), ja genau der mit dem Diagonalargument, hat erhebliche Leistungen in dem Gebiet der Mengenlehre und Unendlichkeit erbracht. Unter anderem hat er bewiesen, dass die Potenzmenge einer unendlichen Menge immer größer ist als die ursprüngliche Menge.2

Die Potenzmenge ist die Menge aller möglichen Teilmengen einer Menge. Hier ist ein Beispiel einer Potenzmenge.


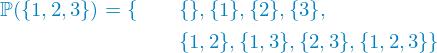
05.png

Die Potenzmenge einer Menge mit lediglich drei Elementen enthält bereits acht Elemente. Die Potenzmenge einer Menge mit 10 Elementen besteht bereits aus 1024 Teilmengen. Im Allgemeinen hat eine Menge der Größe n eine Potenzmenge der Größe 06.png.3

Bereits mit der Potenzmenge lassen sich also immer und immer größere unendliche Mengen konstruieren.

Aleph

Cantor hat auch an einer Notation für unendliche Kardinalzahlen gearbeitet. Er hat hierfür den hebräischen Buchstaben Aleph verwendet.


07.png

Aleph-null ist die Größe der natürlichen Zahlen. Jedes folgende Aleph ist größer als das vorherige. Eventuell fragen Sie sich jetzt, ob Aleph-eins die Größe der reellen Zahlen ist. Die Antwort hierauf ist leider nicht so einfach. Es wurde bisher nicht ohne die Zuhilfenahme einiger Axiome bewiesen, also zusätzlicher Voraussetzungen die nicht beweisbar sind, aber von denen man annimmt, dass sie wahr sind.4 Wir werden hierauf jedoch vorerst nicht weiter eingehen.

Die Aleph-Notation liefert uns einen einfachen Weg absolut wahnsinnig große Kardinalzahlen zu konstruieren. Man kann zum Beispiel Aleph-Aleph-0, also die Aleph-0te unendliche Kardinalzahlen nehmen. Das bedeutet es gibt abzählbar unendlich viele Kardinalzahlen die kleiner sind als diese. Unser mickriger Verstand ist kaum im Stande abzählbare Unendlichkeit zu verstehen, aber wenigstens können abzählbar unendliches zählen. Was wir mit der Aleph-Notation konstruieren können ist jedoch im wahrsten Sinne des Wortes unfassbar.

Ergebnis

Wir haben bewiesen, dass auch die rationalen Zahlen dieselbe Größe haben wie die natürlichen Zahlen, dass sie abzählbar sind. Wir haben jedoch auch festgestellt, dass es tatsächlich mehr reelle Zahlen als natürliche Zahlen gibt, dass die reellen Zahlen überabzählbar sind. Wir haben eine Notation für unendliche Kardinalzahlen kennengelernt und herausgefunden, dass es eine unbegrenzte Anzahl an Kardinalzahlen gibt. Es gibt immer, immer, immer eine größere.

Das war es mit dem rein theoretischen Teil dieser Serie. Beim nächsten mal werden wir uns ein paar interessante theoretische Probleme, die auf der Unendlichkeit beruhen anschauen. Wenn Sie ein Problem/Gedankenexperiment über oder mit Unendlichkeit kennen, dann lassen Sie mir doch ein Kommentar darüber hier und vielleicht werden wir es im nächsten Teil dieser Serie untersuchen.

Sollten Sie der englischen Sprache mächtig sein und Interesse an einer etwas anderen Herangehensweise an Unendlichkeit haben, dann kann ich das YouTube-Video How To Count Past Infinity von VSauce wärmstens empfehlen.

Vielen Danks fürs lesen! Sollte noch irgend etwas unklar sein oder sollten noch Fragen unbeantwortet geblieben sein, dann zögern Sie nicht ein Kommentar zu hinterlassen.

  1. Cantors Diagonalargument - https://de.wikipedia.org/wiki/Cantors_zweites_Diagonalargument
  2. Georg Cantor - https://de.wikipedia.org/wiki/Georg_Cantor
  3. Beweis der Größe von Potenzmengen - https://www.math.utah.edu/~pa/math/sets/powerproof.html
  4. Aleph - https://de.wikipedia.org/wiki/Aleph-Funktion

Gleichungen erzeugt mit latex2png.

#deutsch #science #mathematics #infinity
7 years ago in #de-stem by
$42.75
  • Past Payouts $42.75
  • - Author $32.22
  • - Curators $10.54
97 votes
Reply 3
Sort:  
  • Trending
    • [-]
     7 years ago  

    Congratulations @targodan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :

    Award for the number of upvotes

    Click on any badge to view your own Board of Honor on SteemitBoard.
    For more information about SteemitBoard, click here

    If you no longer want to receive notifications, reply to this comment with the word STOP

    Upvote this notification to help all Steemit users. Learn why here!

    $0.00
      Reply