In diesem kurzen Artikel werden wir formell beweisen, dass die Funktion, die wir in Die Unendlichkeit und noch viel weiter - Teil 2 gefunden haben, eine bijektive Funktion ist. Das Folgende ist nur gedacht für Leser, die gerne einen formellen Beweis sehen würden. In dem ursprünglichen Artikel haben wir bereits informell bewiesen, dass die Funktion bijektiv ist.
Die Funktion
Die gefundene Funktion war definiert wie folgt.
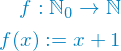
Wir erinnern uns, dass 
und 
.
Injekitvität
Die mathematische definition einer injektiven Funktion:
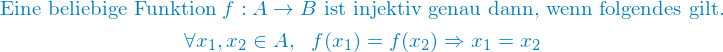
Man ließt "Für alle 
und alle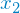 
aus A, 
impliziert 
."
Dies können wir leicht zeigen, indem wir uns von der einen zur anderen Seite durcharbeiten.
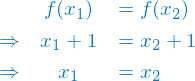
Surjektivität
Die mathematische definition einer surjektiven Funktion.
Man ließt "Für alle y aus B existiert ein x aus A, sodass f(x) = y."
Dies können wir nicht direkt zeigen, also versuchen wir die Funktion zu invertieren und zeigen, dass die Invertierung korrekt ist.
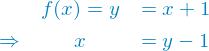
Dies führt zu der inversen Funktion 
. Damit diese Funktion korrekt ist muss folgendes gelten.
Hier können wir wieder einfach von der einen zur anderen Seite arbeiten.
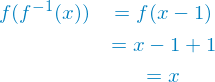
Q.E.D.
Ergebnis
Wir haben soeben bewiesen, dass unsere Funktion sowohl injektiv als auch surjektiv und damit bijektiv ist.
- Injektivität Definition - https://de.wikipedia.org/wiki/Injektive_Funktion
- Surjektivität Definition - https://de.wikipedia.org/wiki/Surjektive_Funktion
PS: Die Abkürzung "Q.E.D." steht für den lateinischen Ausdruck "quod erat demonstrandum", welcher übersetzt "was zu beweisen war" bedeutet.Source Diese Abkürzung ist oft unter mathematischen Beweisen zu finden. Es ist quasi die mathematische Version von "Das Ende".
English version here.
Being A SteemStem Member