Vor kurzem habe ich das Video "Quadratzahlen lernen in nur 10 Minuten" von @humanduck gesehen. Dort beschreibt er einen interessanten Trick, wie man mit dem auswendig Lernen nur jeder dritten Quadratzahl auskommt und trotzdem alle Quadratzahlen schnell abrufen kann. Schaut also mal kurz bei ihm vorbei und lasst euch den Trick erklären.
Wenn es euch so geht wie mir, dann habt ihr euch zwei Fragen gestellt:
- Funktioniert das wirklich mit allen natürlichen Zahlen?
- Wie funktioniert das überhaupt?
Bild Quelle
Lasst uns diese Fragen beantworten
In der Mathematik kommt es oft vor, dass Formeln für die ersten 10 oder manchmal sogar 100 Zahlen funktionieren, doch dann irgendwann zusammenbrechen. Da hilft nur eins: Beweise. Beweise haben den schönen Nebeneffekt, dass sie oft sehr gut verdeutlichen wie etwas funktioniert. Also zwei Fliegen mit einer Klappe für uns.
Aller Anfang ist schwer
Einen Beweis anzufangen ist oft schwer, da es in den meisten Fällen kein Kochrezept für Beweise gibt. Man muss oft improvisieren und in die Trickkiste greifen. Aber keine Angst, der Beweis den wir uns anschauen ist ganz einfach. Nur der Anfang ist immer schwer.
Immer wenn ich nicht auf anhieb sehe, wie ich etwas beweisen kann fange ich einfach mal an aufzuschreiben, was ich denn über das Problem weiß.
Wir haben zwei Fälle, die Unterschieden werden müssen.
Fall 1
Die Zahl, deren Quadratzahl wir suchen ist um eins größer als eine der Zahlen, die wir uns gemerkt haben. Dann addieren wir die Summe der gemerkten und der gesuchten Zahl auf die Quadratzahl der gemerkten Zahl. Oder mathematisch ausgedrückt.
Sei
eine beliebige natürliche Zahl, deren Quadratzahl wir suchen. Wir kennen den Wert von 
.
Hier ist viel Potenzial zur Vereinfachung. Erinnern wir uns also an die zweite binomische Formel und legen los.
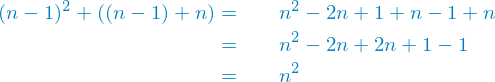
Wir hatten Glück. Der Beweis für diesen Fall ist schon zu ende. Nur durch aufstellen und Umformen der Formel haben wir gerade bewiesen, dass der Trick in diesem Fall für alle natürlichen Zahlen funktioniert. Denn letzten Endes kürzt sich alles weg und nur 
bleibt übrig, was wir ja ursprünglich durch den Trick berechnen wollten.
Fall 2
Die Zahl, deren Quadratzahl wir suchen ist um eins kleiner als eine der Zahlen, die wir uns gemerkt haben. Dann subtrahieren wir die Summe der gemerkten und der gesuchten Zahl von der Quadratzahl der gemerkten Zahl. Oder mathematisch ausgedrückt.
Sei
eine beliebige natürliche Zahl, deren Quadratzahl wir suchen. Wir kennen den Wert von 
.
Wieder formen wir um und Vereinfachen. Diesmal benötigen wir die erste binomische Formel.
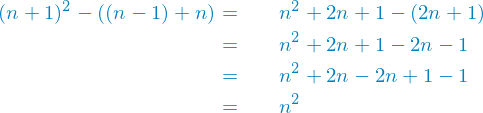
Et voilà, auch hier bleibt am Ende wieder nur stehen. Also funktioniert auch dieser Fall für alle natürlichen Zahlen.
Ergebnis
Wir haben gerade Bewiesen, dass der Trick von @humanduck für alle natürlichen Zahlen funktioniert. Wie funktioniert der Trick? Es ist einfach eine kompliziertere Formel für das berechnen der Quadratzahl. Diese Formel ist zwar komplizierter auf dem Papier, aber viel einfacher im Kopf zu berechnen, wenn wir jede dritte Quadratzahl bereits kennen.
Vielen Dank fürs Lesen! Sollte etwas unklar sein, oder solltet Ihr noch Fragen haben, dann lasst mir einfach ein Kommentar hier und ich werde mein Bestes geben, alle Fragen zu beantworten.
You got a 86.96% upvote from @inciter courtesy of @targodan!
Sehr schöner Beitrag ;)