DTube: Integral of ∫√(a^2 - x^2)dx using a Trigonometric Substitution

What I love about mathematics is some of the very creative and ingenious methods that someone has come up with to find solutions to perplexing problems.

The integral of √(a² - x²) is a great example one of these problems. If you look up a table of integrals, you may find the solution to look something like this...

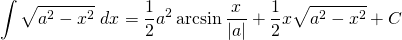
Well, you might expect √(a² - x²) to be in the answer, but how did the term arcsin(x/a) get in there? How did we start with a purely algebraic expression, and end up with one having a trigonometric function?

You might have also guessed we needed to make a substitution in order integrate this function. So the answer lies in the approach to the substitution. If we simply made the substitution...

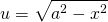
... we would quickly run into problems. We need another approach.

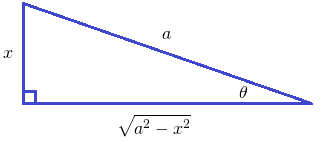
If you consider √(a² - x²) as an expression for solving a Pythagorean Theorem problem, we can set up a right-angle triangle where a is the hypotenuse, and x as the length of the vertical side, as depicted above.

From trigonometry, sinθ = x/a. So, what if we made the substitution x = asinθ? We get...

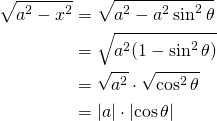
Geometrically, a must be positive, but it doesn't have to be numerically. This is not of any significant consequence since the squaring of a turns it positive everywhere else. Let's just assume that a is positive, so we can drop the absolute value bars.

Let's also assume that...

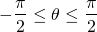
...which means that...

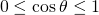
...and thus we can drop the absolute value bars on the cosθ term. Thus the integrand becomes...

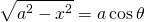
Now, we need a substitution for dx as well. So we simply take the derivative of x = asinθ.

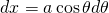
So, the integral becomes...

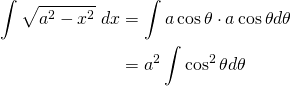
Now, to integrate cos²θ, we need the half-angle formula...

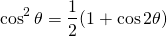
Substituting this in, we get...

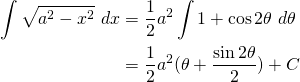
Now, another trigonometric identity is...

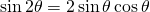
Putting this in, we get...

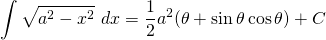
Before we finish, we need to get everything back in terms of x's, rather than leave the solution in terms of θ's. We established that...

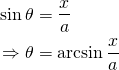
Also from trigonometry...

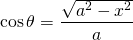
Then finally...

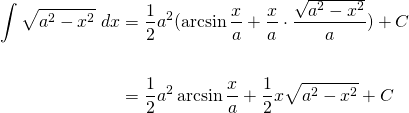
Wow! That was quite a process. If you need a clearer explanation, play my video.

Thanks for watching. Please give me an Upvote and Resteem if you have found this video helpful.

Please ask me a math question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3

► Watch on DTube
► Watch Source (IPFS) Tip me at PayPal: https://paypal.me/MasterWu