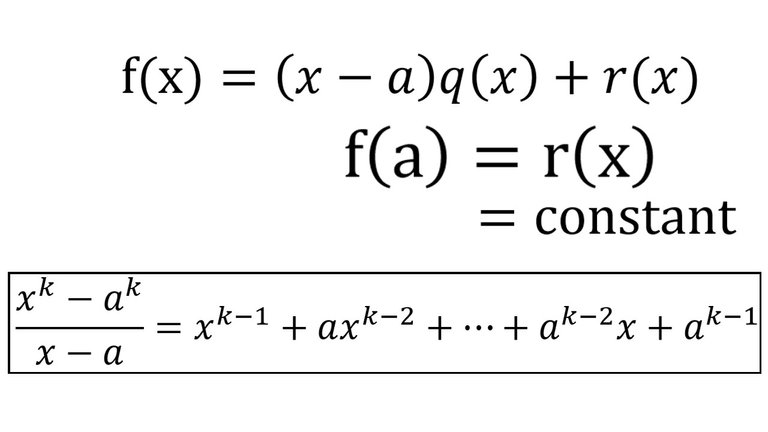
NOTE: This is a re-upload because the previous video (
) was in AVI format but apparently that doesn't work on DTube so I've re-uploaded in MP4.In this video I go over a second proof of the Polynomial Remainder Theorem which I derived in my earlier video but this time look at a what is sometimes referred to as a more “elementary” proof. In my earlier video I used the Euclidean Division theorem for Polynomials to show that the remainder of a polynomial f(x) divided by the polynomial (x – a) is simply equal to f(a), and hence is a constant. But in this video I take a look at a more “basic” approach, hence the term “elementary”, in deriving this very same theorem. From my last video I showed that (x – a) is a factor of the polynomial of the form (x^k – a^k). This becomes useful since the subtraction f(x) – f(a) is simply a linear combination of polynomials of that very same form. This means that f(x) – f(a) can be divided cleanly by (x – a) thus resulting in a quotient, q(x). Rearranging the resulting formulation we obtain f(x) = q(x)(x – a) + f(a) where f(a) is our remainder, thus proving the theorem! This is a very unique approach to deriving the polynomial remainder theorem and is always great to learn the many different ways of deriving the same theorem, so make sure to watch this video!
Download the notes in my video: https://1drv.ms/b/s!As32ynv0LoaIh4ItFjOYuitEy7DWoA
View Video Notes on Steemit: https://steemit.com/mathematics/@mes/polynomial-remainder-theorem-elementary-proof
Related Videos:
Polynomial Long Division: (x - a) is a factor of (x^k - a^k) PROOF:
Euclidean Division of Polynomials: Theorem and Proof:
Polynomial Remainder Theorem: Proof + Factor Theorem:
Polynomials - A Simple Explanation:
Polynomial Long Division - In depth Look on why it works!:
Polynomial Long Division - Examples:
Factoring Quadratic Polynomials by Guessing:
Direct Substitution for Polynomials - Simple Proof:
Polynomial Long Division: Multiple Variables: .
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
Like, Subscribe, Favorite, and Comment Below!
Follow us on:
Email me: [email protected]Official Website: https://MES.fm
Steemit: https://steemit.com/@mes
Gab: https://gab.ai/matheasysolutions
Minds: https://minds.com/matheasysolutions
Twitter: https://twitter.com/MathEasySolns
Facebook: https://fb.com/MathEasySolutions
Google Plus: https://mes.fm/gplus
LinkedIn: https://mes.fm/linkedin
Pinterest: https://pinterest.com/MathEasySolns
Instagram: https://instagram.com/MathEasySolutions
Try our Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Try our Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
▶️ DTube
▶️ IPFS
I don’t always prove the polynomial remainder theorem but when I do I usually follow up with a more “elementary” derivation ;)
View Video Notes on Steemit: https://steemit.com/mathematics/@mes/polynomial-remainder-theorem-elementary-proof
Thank you!You really helped me understanding :)
Very interesting post.