Yes, you read that right. Game Theory. And it’s not about games; well, it is. But not about the games you know. Here, the word “game” means “every interaction between two people or agents, in which the decision of each one depends on the other one’s decision”.

Economists love Game Theory, because, boiled down to its most basic definition, it is the study of decisions and how they are made.
Economists are well known for having a special kind of thinking, one involving concepts such as opportunity cost, the marginal principle, the famous ceteris paribus (which means “everything else remaining constant”), incentives and utilitarianism in general ingrained as a general principle.
Game Theory is a field that encompasses all of the concepts, principles, and things that make Economics an interesting social science. We as Economists love to assign values to things, to optimize and to maximize. The same happens in Game Theory. Because in Game Theory we’re always searching for the best possible response of one agent in response to the other one. Once we get his result, we shall call it the Nash Equilibrium, which ensures that no matter the decision of the other person, our person will always get the best response when compared to its other available options.

Maybe the best example of Game Theory is the popular Prisoner’s Dilemma, in which two thieves have been arrested, and each one is interrogated in private. The interrogators tell each thief that if he confesses about his partner in crime, and if this partner doesn’t confess, he won’t have to serve any amount of years in prison, and his partner will have to be 10 years in prison. Now, if he confesses, but at the same time, his partner confesses as well, both of them serve 8 years in prison.
The other options are that none of them confesses, in which case they just have to serve 1 year in prison.
Given this situation, Game Theory will always say that the Nash Equilibrium (the optimal response of eac1h agent no matter the answer of the other person), is always confessing. Depressive, right?
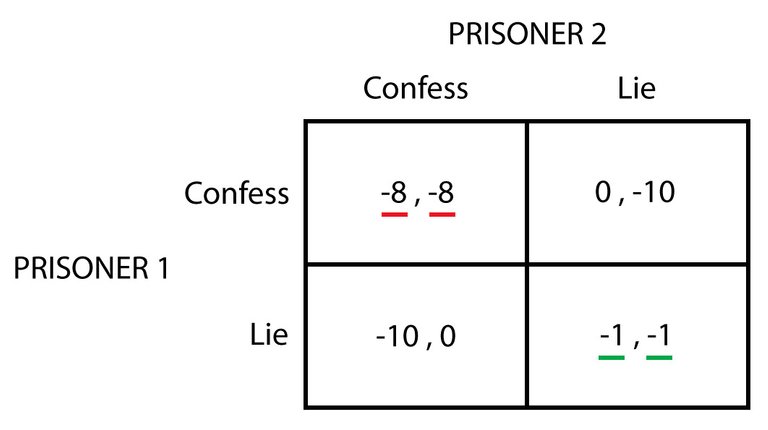
But it is actually the best available option. Game Theory would make us represent this situation in a grid to decide the best available option for each thief (or prisoner in this case):
Of course, this isn’t the end of the story, in Game Theory you also have cooperative games instead of competitive games such as the Prisoner’s Dilemma. Cooperative games are more concerned about coalitions, how to reward each member, etc. For this there are a lot of interesting principles and a new concept instead of our Nash Equilibrium, this is the Shapley Value, which “assigns a unique distribution (among the players) of a total surplus generated by the coalition of all players. The Shapley value is characterized by a collection of desirable properties.”
In our daily lives, we always use Game Theory, the difference is that we don’t tend to rationalize the process of making a decision. Game Theory, as a study field, is not only useful for the Economic Sciences, but also for the military, psychology, and basically every situation that involves having to make a decision when other people, business or economic agent is involved.
Cool read :) just testing something - !tip
Check out @cardboard blog here and follow if you like the content :)
Sending tips with @tipU - how to guide :)
🎁 Hi @freedomanytime! You have received 0.1 STEEM tip from @cardboard!