Hi Everyone,

Welcome to the sixth post in my conference and journal paper post series. This series will contain ten conference and journal papers from my time working in the Queensland Government. In my post, My Peer Reviewed Conference and Journal Papers, I explain the purpose of this series.
In 2014, I published and presented three papers. I presented two at the ARRB Conference and one at the European Transport Conference. The paper, Is Road Infrastructure That Improves Operating Speed a Double-Edged Sword When It Comes to Road Safety?, was one of the papers I presented at the ARRB Conference. The paper went through the scrutiny of Transport and Main Roads. This was not a problem, as I did not discuss any particular project or even mention the department or the Queensland Government. Instead, the paper focused on data and the relationship between speed and various types of road crashes.
The previous year’s paper was the incentive for this paper. A key failing of the Bruce Highway Action Plan (BHAP) was the added danger to motorists from higher operating speeds. The BHAP projects would reduce the number of road crashes but increase their severity because the crashes would occur at a higher speed. Therefore, road safety should not be assessed on just the impact on the number of accidents but also their severity.
The paper was well received by the conference, and it aligned with the shift towards greater analysis of crashes and the costs of these crashes. However, I do not know the extent to which this approach has been adopted by economists conducting cost benefit analysis. It is most likely adopted when isolating crash types increases the benefits of a project. For example, a safety focused project. If the project were focused on reducing travel times, a simple analysis on the reduction of crashes would most likely be used. The Government would not want to pay for a cost benefit analysis that indicates that their projects could be costing lives even if that were the most likely outcome. I say this based on my experience working on BHAP.
IS ROAD INFRASTRUCTURE THAT IMPROVES OPERATING SPEED A DOUBLE-EDGED SWORD WHEN IT COMES TO ROAD SAFETY?
ABSTRACT
Building new or upgrading existing road infrastructure is a common practice to reduce congestion and improve travel time. Road infrastructure projects that successfully improve operating speeds throughout the day or just during peak periods also have an impact on safety.
This paper aims to address how new or upgraded road infrastructure primarily constructed to improve operating speed impacts road safety. Is road safety improved, worsened or negligibly changed? Literature indicates that higher speeds increase the severity of road accidents but new and upgraded road infrastructure is generally built to a standard that will reduce the probability of accidents occurring. Does the reduced probability of an accident occurring offset the more severe accidents likely to occur from the higher operating speeds? The matter is further complicated when the new or upgraded infrastructure eliminates particular severe accident types that occur even at lower speeds such as head-on collisions on existing single carriageway roads.
In this paper, three types of road projects are considered, town bypasses, duplication of carriageways and overtaking lanes. These three types of projects have been selected due to the different nature of safety implications for each project type. The accident costs for each of these projects have been calculated using both the Austroads’ human capital approach and Hensher’s willingness to pay approach. Reductions in accidents are calculated based on model road state (MRS) and percentage reductions based on particular treatments. The safety implications for projects may not be as predictable as one would expect.
1. INTRODUCTION
This paper investigates the relationship between improved infrastructure, primarily designed to improve vehicle operating speed, and safety. The key relationships investigated are speed, accident1 rate, accident severity and treatments incorporated in the infrastructure upgrades. There is an abundance of safety data available and this data is relatively detailed. Date of accident, severity of accident, type of accident (according to code) and location of accident are normally readily available. The relationship between vehicle speeds, accidents and accident severity cannot easily be established, as the speed of the vehicle during impact is not normally available. The speed limit can act as a proxy to determine a breakdown of accident types and severity at various speeds if the speed limit is the key determinate of operating speed. Unfortunately, speed limit is not a strong proxy for operating speed when roads are close to capacity and vehicles are operating at speeds well below the posted speed limit. Literature suggests that higher speed limits result in more severe accidents. Can this same relationship be applied to operating speed?
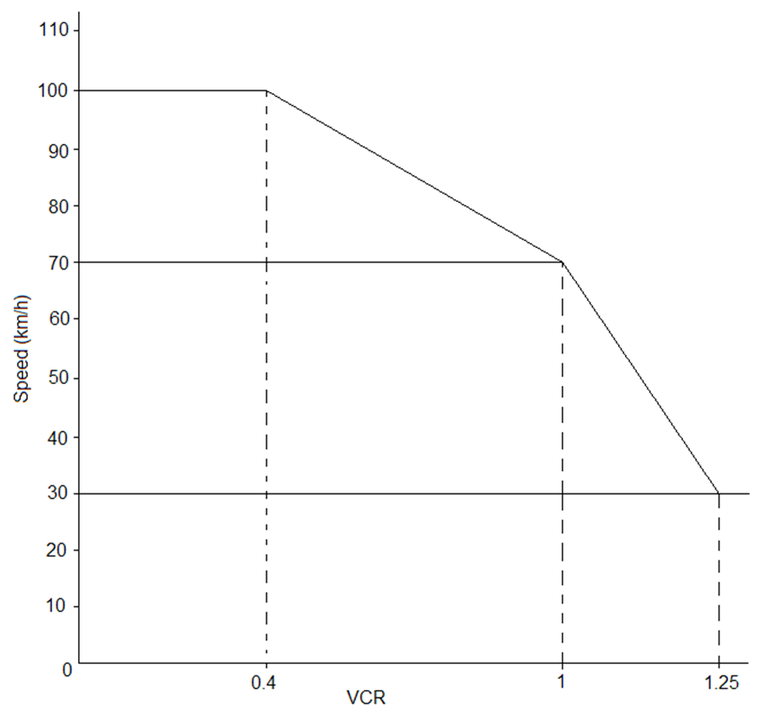
In this paper, accident data has been collected from highways and motorways from around South-east Queensland (SEQ).This data is grouped according to a calculated average operating speed at the locations of the accidents. The calculated operating speed relies upon the relationship between operating speed and the volume capacity ratio (VCR). This ratio can be calculated based on the traffic volume and capacity of the highway. Accident rates based on the severity for each band of operating speeds are calculated. These accident rates are used to determine the average cost per million vehicle kilometres travelled (mVKT). The aim of determining the accident rates and costs for various bands of operating speed is to determine how changes in operating speed affects frequency and severity of accidents.
The paper applies the calculated accident rates and costs per mVKT to three hypothetical case studies of projects that aim to improve operating speed. Two approaches to estimating the costs of accidents has been applied to the case studies. The first approach is the Austroads human capital (HC) approach and second is the Hensher willingness to pay (WTP) approach. Two credible approaches have been applied with varying values for accidents of different severity to help determine if the overall safety of the road can be consistently stated as improved by the project.
2. LITERATURE REVIEW
Road infrastructure upgrades generally improve or add to existing infrastructure to improve operating speed. Road infrastructure designed to increase capacity and increase operating speeds follow engineering standards that are intended to either mitigate or reduce severity of accidents. Hauer (1997) considers the impacts of treatments on safety by comparing projected accidents based on regressed trends in historical data to actual accidents on the completion of a particular treatment. RTA (2004) established percentage reductions for various treatments according to accident type. These accident types are classified according to definitions for classifying accidents (DCA) or road user movement (RUM). Andreassen (1993) noted that treatments could affect frequency of accidents or the distribution of injury severity. A treatment that reduces the frequency of an accident type that has a high percentage of fatalities will reduce the accident rate and accident severity of accidents expected to occur at the site of that treatment. In the absence of changes to operating speed, new road infrastructure is expected to improve safety.
The next step is to determine the impacts operating speed has on safety in the absence of any new infrastructure. Austroads (2012) Guide to Project Evaluation contains costs per crash stereotype for RUM at various speed limits for Western Australia and costs per crash stereotype for DCA codes at various speed limits for Victoria. The higher speed limits have higher costs per crash figure across all reported accident types for both Western Australia and Victoria. Crashes by severity were also provided for Victoria according to speed limit. Higher speed limits produced higher percentages of accidents resulting in fatalities or hospitalisation; Table 1 contains accident severity for Victoria according to speed limit. Evidence produced by Austroads (2012) strongly indicates a positive relationship between speed limits and crash severity. Speed limits and operating speed normally have a positive relationship implying operating speed and crash severity have a positive relationship.
Table 1: Accident Severity based on Speed for Victoria, Australia.
Speed Limit (km/h)| Killed | Hospitalised | Other Injury | Total Causalities | Not Injured
| <50 | 0.20% | 16.10% | 32.20% | 48.50% | 51.50%
| 50 | 0.40% | 19.50% | 33.50% | 53.40% | 46.60%
| 60 | 0.50% | 17.90% | 32.00% | 50.30% | 49.70%
| 70 | 0.70% | 19.20% | 30.00% | 49.90% | 50.10%
| 80 | 1.00% | 20.00% | 31.00% | 52.00% | 48.00%
| 90 | 1.70% | 26.90% | 30.40% | 59.00% | 41.00%
| 100 | 3.20% | 30.10% | 33.00% | 66.30% | 33.70%
| 110 | 3.50% | 28.00% | 33.50% | 64.90% | 35.10% |
Research conducted by Kloeden et al (1997) indicated that the risk of casualties doubled every 5km/h above 60km/h in a 60km/h speed limit zone. This observation by Kloeden et al (1997) implies a relationship between speed and casualties but more strongly indicates the relationship between speeding and casualties. However, congestion and speeding would expected to be negatively related. Examples of changes in policy provide an indication of the relationship between speed and road safety. In the USA, in 1974, the government reduced the maximum national speed limit to 55mph as an attempt to reduce fuel consumption. Road fatalities also happen to fall by 16.4%, there were 45,196 fatalities in 1974 compared to 54,052 in 1973 (Friedman et al 2009). Since 1995, USA federal speed limits have been removed from roads. The number of fatalities has also increase substantially. Friedman et al (2009) estimated that the higher speed limits account for an additional 12,545 deaths over a 10-year period. Can we assume congestion related restrictions to operating speed have the same effect on crash severity as speed limits? Andreassen (1992) calculated the mean costs per accident per accident categories for repairs and casualty for rural and urban areas. He found that the percentage of accidents that resulted in fatalities and hospitalisation were higher in rural areas than urban areas. Urban environments have lower average operating speeds than rural areas due to less congestion and higher speed limits. It is still possible that factors other than operating speed, such as driver fatigue or conditions or quality of rural roads, contribute to the higher fatality and injury rates in rural areas. Another approach would be to consider the relationship between accidents and traffic volume in the same environment. Kononov, Bailey and Allery (2008), established a relationship between accidents per mile per year (APMPY) and traffic volume for freeways in the USA. Their findings indicated a strong positive relationship between APMPY for total accidents and average annual daily traffic (AADT) but such a relationship did not exist for injuries and fatalities once the level of service (LOS) for the highway fell to F2 , indicating congestion may reduce the probability of accidents causing serious injuries. Consistent with Kononov, Bailey and Allery’s findings regarding LOS, Shefer and Rietveld (1997) observed that the number of fatalities did not spike during the peak periods of the days. Instead, the number of fatalities was lower in the morning peak and remained constant from around 2PM to 2AM before dropping to AM peak numbers. Fatality statistics for 2011 and 2012 from the Department of Infrastructure and Regional Development (2014) follow a very similar pattern to those observed by Shefer and Rietveld (1997). The lack of spikes in fatalities during peak periods indicates that factors other than traffic volume are influencing the number of fatal accidents. The most obvious factors to consider would be changes in speed or increased fatigue as the day ends. Average speeds are lower during peak periods; a positive relationship between speed and fatalities is a possible explanation. Fatigue related accidents could explain the drop in morning peak accidents but it does not explain why fatality rates did not continue to increase from mid-afternoon to the afternoon peak. Wang (2010) found, with his study of the M25 in the UK, that there was a positive relationship between congestion and the frequency of serious injuries occurring from accidents but did not have sufficient data to determine a relationship between congestion and fatalities. As with other studies, Wang (2010) established a strong relationship between AADT and frequency of accidents. The objective of Wang’s thesis was to determine if the problems of congestion and safety can be reduced simultaneously. He also investigated the impact new engineering standards have on reducing accidents drawing similar conclusions to Hauer (1997). Evidence generally suggests that higher operating speeds are likely to produce accidents of a more serious nature. What impact do higher operating speeds have on accident rate? Navon (2003), identified that the accident rate increases with the number of interactions between vehicles such as passing in the same or opposite direction. He found that the number of interactions are higher at lower average operating speeds. Aarts and Schagen (2006), found that the accident rate increased as operating speed increased. Their work involved the collecting and collating work from other various studies to draw their conclusions. They also found that accident rates increased when there was a greater variance in speed of vehicles travelling. According to Marchesini and Weijermars (2012), there is a perception that crash frequency increases with congestion levels. They also observed that crash severity is less within queues than at the end of queues. Lee, Hellinga and Saccomanno (2003), found accidents were more closely related to changes in speed within the queue rather than directly to the average speed of the queue. Accident rates seem more closely related to the cause of the reduction in operating speed and fluctuations in operating speed rather operating speed itself. 3. ESTABLISHING A RELATIONSHIP BETWEEN SAFETY AND OPERATING SPEEDCurrent literature strongly implies a positive relationship between operating speed and accident severity but the relationship between operating speed and accident frequency is less clear. The relationships discussed in the literature review are tested in the context of South-east Queensland (SEQ) motorways and highways. Motorways and highways have been selected because of the consistently higher speed limits and lack of intersections. The high speed limits of the motorways are an important consideration to isolate accidents related to operating speed influenced by lack of road capacity. The exclusion of intersections was also an important factor as intersections have different accident severity and rates to mid-block sections of road, to include them would distort the analysis. Existing mid-block treatments along the selected motorways and highways are included in data and are reflected in the aggregate results presented. Table 2 contains the sections of highways/motorways incorporated in the analysis. Table 2: Motorway and length of motorway considered in the analysis.
|
|---|