OBJETIVOS
Objetivo general
este proyecto se centró en el modelamiento matemático a partir de ecuaciones diferenciales de segundo orden en la deflexión de vigas.
Objetivos específicos
-determinar la deflexión teóricamente, para ser comparada con la experimental.
-Probar que las ecuaciones diferenciales sirven en la cotidianidad, como por ejemplo la deflexión de vigas.
JUSTIFICACIÓN
Debido a que las ecuación diferenciales tienen aplicaciones en diferentes aspectos de la vida cotidiana, se tiene la motivación de emplear las ecuaciones diferenciales de segundo orden para demostrar que uno de las tantas aplicaciones es la deflexión de vigas y con el modelamiento exacto se obtienen beneficios para diferentes usos como poder calcular el punto máximo de deflexión, aplicando el diseño de estructura, ubicación de puntos estratégicos donde colocar arcos y optimización de materiales. La práctica de deflexión es muy usada para determinar las propiedades de los materiales como son la flexibilidad. Tenemos un módulo de elasticidad y una resistencia a la flexión. El ensayo de deflexión se basa en la aplicación de una fuerza puntual y simplemente apoyada, para determinar la resistencia del material hacia una carga estática o aplicada lentamente. La Resistencia de Materiales es de gran importancia en el campo de la ingeniería, ya que proporciona los criterios necesarios para el análisis de esfuerzos y deformaciones de sistemas mecánicos, lo cual es fundamental para el diseño, análisis de falla y evaluación de elementos mecánicos.
Orígenes de la teoría de la elasticidad de las vigas.
Todos los cuerpos reales se deforman bajo la aplicación de una carga, elástica o plásticamente. Un cuerpo puede ser tan insensible a la deformación que el supuesto de rigidez no afecte en grado suficiente a un análisis para asegurar un tratamiento no-rígido. Si después se comprueba que la deformación del cuerpo no era despreciable, entonces la declaración de rigidez fue una decisión errónea, no un supuesto equivocado. Un cable metálico es flexible, pero en tensión puede ser prácticamente rígido y se distorsiona mucho si se somete a cargas de compresión. El mismo cuerpo puede ser rígido o no rígido. El análisis de la deflexión influye en las situaciones de diseño en muchas formas. A menudo, el tamaño de una pieza se determina de acuerdo con las deflexiones, en vez de calcularse con base a los límites de esfuerzo y algunas veces, los elementos mecánicos se diseñan para que tengan una característica particular de la relación fuerza-deflexión.
Uno de los grandes contribuyentes en descubrir el cambio de posición que tiene una viga bajo una fuerza fue Charles August COLOUMB (1736-1806), físico que junto con NAVIER son creadores de la Resistencia de los materiales.
En 1776, publicó el primer análisis correcto de los esfuerzos en una viga con sección rectangular. Aplicó la ley de Hooke a las fibras, situó la superficie neutra en su posición correcta, desarrolló el equilibrio de las fuerzas en la sección con las fuerzas externas y evaluó que en la falla, bajo ciertas condiciones, la superficie neutra debería moverse a otra posición. Se necesitaron 135 años desde que galileo hiciera el primer intento de solucionar el problema.
Thomas YOUNG (1733-1829), en Cambridge, introdujo por primera vez el concepto de módulo de elasticidad, con una definición muy diferente a la que conocemos hoy en día: “El módulo de Elasticidad de cualquier sustancia es una columna de la misma sustancia, capaz de producir una presión en su base que es al peso que causa cierto grado de comprensión como la longitud”. Así mismo, trató problemas de torsión de ejes y flexión de vigas en voladizo y el problema de la tensión y comprensión excéntrica de barras de sección rectangular.
Louis Marie Henri NAVIER (1785-1836), ingeniero, matemático y profesor, publicó, en 1826, la primera edición de sus “Lecons”, el primer gran texto de mecánica den la ingeniería. No sólo presentaba un buen tratado sobre la resistencia y las deflexiones de las vigas de cualquier sección, sino que consideraba arcos, columnas con cargas excéntricas, puentes colgantes y muchos problemas técnicos. A Navier le corresponde el honor de desarrollar la primera teoría general de los sólidos elásticos, así como el primer tratamiento sistemático de la teoría de estructuras.30
Otros tres ingenieros, Lamé, Saint-Venant y Duhamel, fueron pioneros en el desarrollo de la Teoría de la elasticidad. LAMÉ publicó el primer libro sobre “elasticidad” y, junto con CLAPEYRON, introdujo el concepto de igualdad del trabajo externo e interno en una estructura deformada.
FORMULAS ECUACIONES DIFERENCIALES SEGUNDO ORDEN:
No importa cuál lado de x se tome puesto que los momentos flectores calculados desde cualquier lado son iguales. El momento flector en x está simplemente relacionado con el radio de curvatura de la curva elástica en x, siendo la relación:
Donde E es el módulo de elasticidad de Young y depende del material usado en el diseño de la viga, e I es el momento de inercia de la sección transversal de la viga en x con respecto a una línea horizontal que pasa por el centro de gravedad de esta sección transversal. El producto EI se llama la rigidez y se considerará como una constante. Si asumimos que la viga se dobla sólo levemente, lo cual es válido para muchos propósitos prácticos, la pendiente y’ de la curva elástica es tan pequeña que su cuadrado es despreciable comparado con 1, y la ecuación se puede remplazar por la buena aproximación:
Entonces,
El momento flector M(x) es la suma algebraica de los momentos de estas fuerzas actuando a un lado del punto P.
Escogiendo el lado derecho de P, actuarían dos fuerzas:
1-La fuerza hacia abajo w (L - x), a una distancia (L -x)/2 de P, produciendo un momento positivo.
2-La fuerza hacia arriba w (L/2), a una distancia L-x de P, produciendo un momento negativo. En este caso el momento flector es:
Con el valor de M(x), la ecuación fundamental es:
Dos condiciones son necesarias para determinar y. Estas son, y = 0 en x = 0, y en x = L, puesto que la viga no tiene deformación en los extremos o apoyos.
Integrando dos veces se obtiene
Puesto que y = 0 cuando x = 0, tenemos c2 = 0. De donde
Puesto que y = 0 cuando x = L, c1 = wL3 /24 y tenemos, finalmente:
Como la ecuación requerida de la curva elástica. Es de interés práctico usar la solución final para hallar la máxima deflexión. De la simetría o por el cálculo, el máximo ocurre en x = L/2, de donde la flecha máxima será:
En nuestro proyecto se tiene una tabla
EI= CONSTANTES
EI = constante E = 2,8* 109 kg/m² I = 21.3*10-3
E= módulo de Young de elasticidad de la viga. I= momento de inercia de un corte transversal de la viga.
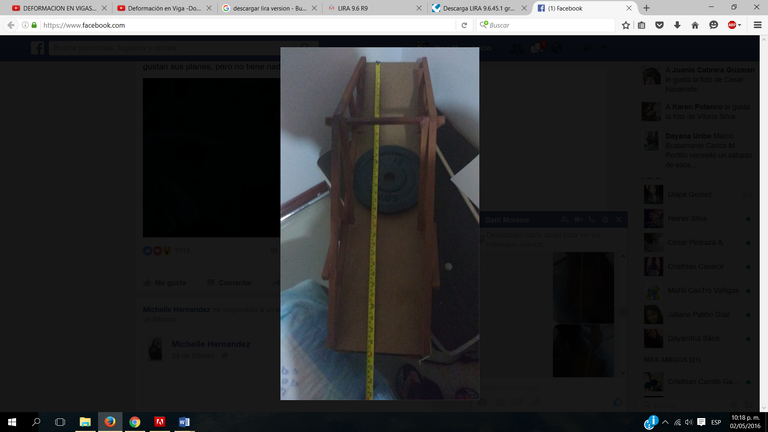
X= 0.45m Este dato lo obtuvimos del punto centro de la tabla de madera ya que en este se encuentra el peso del sistema
Y= 0.91m Longitud de la tabla donde se apoya el peso
W= 10kg
Peso del disco del sistema
=
En la formula anterior reemplazamos cada dato en las variables establecidas, dejamos la masa del disco en kilogramos (kg), las medidas de la tabla las tomamos en metros (m) y finalmente reemplazamos EI que son constantes del sistema, hay que tener en cuenta que E varia según el material que se emplea para la deflexión.
% ERRROR
= %
Experimentalmente medimos la distancia que se ha flexionado la madera teniendo en cuento un cordón blanco como punto de inicio.
Análisis de resultados
• Realizando todas las mediciones se puede llegar a la conclusión que el peso es directamente proporcional a la distancia de flexión de la viga.
• El porcentaje de error es del 7.69% obtuvimos poco error, esto demuestra que si empleamos bien las ecuaciones diferenciales.
• El modelo de Young realmente funciona si se realizan los cálculos y se encuentra el E del material correcto.
• Los cálculos varían dependiendo del apoyo que sostenga la viga, su momento(M) cambia dependiendo si son rodillos, asadores o empotramientos.
Congratulations @thegomezmora! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard: