Cryptocurrencies like Bitcoin or Litecoin, etc use the Elliptic Curve (EC) to calculate the public keys.
Elliptic Curve Cryptography (ECC) was invented by Neal Koblitz and Victor Miller in 1985.
A 256-bit ECC public key should provide comparable security to a 3072-bit RSA public key thus less processing power is required. Elliptic curves are called elliptic because of their relationship to elliptic integrals in mathematics. Elliptic curves have nothing to do with ellipses. Ellipses are formed by quadratic curves (x2). Elliptic curves are always cubic (x3).
Cryptocurrencies uses the following elliptic curve equation: y2 = x3 + ax + b
Elliptic curve domain parameters over Fp associated with a Koblitz curve secp256k1
Documented by the Standards for Efficient Cryptography Group (www.secg.org)


Elliptic curve properties
If a line intersects two points P and Q, it intersects a third point on the curve -R.
If a line is tangent to the curve, it intersects another point on the curve.
All vertical lines intersects the curve at infinity.
Adding two distinct points P and Q on an elliptic curve (P ≠ Q)
Fig. 1 Geometry approach
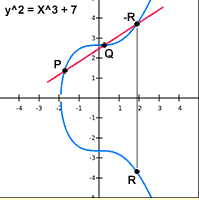
Draw a straight line between P (x1, y1) and Q (x2, y2).
The line will intersect the elliptic curve at exactly one more point -R (x3, -y3).
The reflection of the point -R with respect to x-axis gives the point R (x3, y3), which is the results of addition of points P and Q.
Mathematical approach
The point slope form of the line:
λ = ( y2 - y1 ) / ( x2 - x1 )
λ ( x2 - x1 ) = ( y2 - y1 )
Let ( x, y ) be any point on the curve. Repace (x2, y2) with ( x, y ):
λ ( x - x1 ) = ( y - y1 )
The slope-intercept form of the line:
λ ( x - x1 ) + y1 = y
λx - λx1 + y1 = y
λx + y1 - λx1 = y [Equation 1]
Create variable: β = y1 - λx1
Implement variable β in Equation 1:
y = λx + β [Equation 2]
Finding coordinates point R (x3, y3):
y = λx + β
y2 = ( λx + β )2
the ellipc curve: y2 = x3 + ax + b
( λx + β )2 = x3 + ax + b
( λx )2 + 2βλx + β2 = x3 + ax + b
x3 + ax + b - ( λx )2 - 2βλx - β2 = 0
x3 - λ2x2 + ax - 2βλx + b - β2 = 0
x3 - λ2x2 + (a - 2βλ)x + (b - β2) = 0 [Equation 3]
Equation 3 represents a monic polynomial, it means is that the coefficient of the highest power of x which is x3 is 1. A property of monic polynomials is that the sum of their roots (x1, x2, x3) is equal to the negative of the coefficient of the second highest power.
Notice that the coefficient of x2 is -λ2, thus:
x1 + x2 + x3 = λ2
x3 = λ2 - x1 - x2
x3 and y3 must be on the straight line y = λx + β:
y3 = λx3 + β
y3 = λx3 + (y1 - λx1)
y3 = λ(x3 - x1) + y1
Point -R has the coordinate (x3, -y3). The reflection of the point -R with respect to x-axis gives the point R (x3, y3), which is the results of addition of points P and Q.
This means you need to multiple y3 with -1:
y3 = λ(x1 - x3) - y1
Implement modulo p to limit points (xR, yR) in finite field Fp:
A straight line will intersect an elliptic curve at three points P (x1, y1), Q (x2, y2) and -R (x3, -y3).
The reflection of the point -R with respect to x-axis gives the point R (x3, y3), which is the result of addition of points P and Q.
λ = ( y2 - y1 ) / ( x2 - x1 )
x3 = λ2 - x1 - x2
y3 = λ(x1 - x3) - y1
Make point Q the same as the Generator point G (see secp256k1 elliptic curve domain parameters), repace point P coordinates (x1, y1) with ( x, y ) to indicate it can be any coordinate on the curve and R coordinates (x3, y3) with (xR, yR) the equations will look like:
λ = ( yG - y ) / ( xG - x)
xR = λ2 - x - xG
yR = λ(x - xR) - y
The last three math operations may output real numbers (ℝ).
Real numbers are numbers that can be positive or negative and have decimal places after the point.
Example: ℝ = {..., -5, -2.5, 0, 3, 6.334, ...}.
In ECC we never work with real numbers only with integers (ℤ) so there are no inaccuraties due to rounding errors.
Integers are positive numbers and have no decimal places after the point.
Example: ℤ = {0, 1, 2, 3, ...}
To make the calculations go faster a finite number of integers are to be used (Fp).
The finite field (Fp) make working with curves a completely different concept.
The curves when graphed over a finite field do not even resemble fig 1.
When modulo p is applied, the equations of adding two points (ECAdd) will look like:
λ = ( yG - y ) modinv( xG - x) (mod p)
xR = λ2 - x - xG (mod p)
yR = λ(x - xR) - y (mod p)
Doubling point P on an elliptic curve. Same as moving point Q to the same location as point P (P = Q)
Fig. 2 Geometry approach
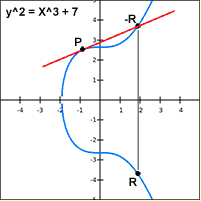
Draw a tangent line to the elliptic curve at point P.
The line intersects the elliptic curve at the point -R.
The reflection of the point -R with respect to x-axis gives the point R, which is the results of
doubling of point P.
Mathematical approach
The slope of the tangent at a point P (x1, y1):
The ellipc curve: y2 = x3 + ax + b
2ydy = 3x2dx + a
a = 0, see secp256k1 elliptic curve domain parameters
2ydy = 3x2dx
(2ydy)/dx = 3x2
(dy/dx) = (3x2)/(2y)
λ = (dy/dx)
λ = (3x2)/(2y)
λ = (3x12)/(2y1)
Finding coordinates point R (x3, y3):
Equation 3 represents a monic polynomial, it means is that the coefficient of the highest power of x which is x3 is 1. A property of monic polynomials is that the sum of their roots (x1, x2, x3) is equal to the negative of the coefficient of the second highest power.
Notice that the coefficient of x2 is -λ2, thus:
x1 + x2 + x3 = λ2
But point Q (x2, y2) is the same as point P (x1, y1), thus:
x1 + x1 + x3 = λ2
x3 = λ2 - 2x1
x3 and y3 must be on the straight line (see Equation 2): y = λx + β:
y3 = λx3 + β
y3 = λx3 + (y1 - λx1)
y3 = λ(x3 - x1) + y1
Point -R has the coordinate (x3, -y3). The reflection of the point -R with respect to x-axis gives the point R (x3, y3), which is the results of doubling of point P.
This means you need to multiple y3 with -1:
y3 = λ(x1 - x3) - y1
Implement modulo p to limit points (xR, yR) infinite field Fp:
The tangent line will intersect an elliptic curve at points P (x1, y1) and -R (x3, -y3).
The reflection of the point -R with respect to x-axis gives the point R (x3, y3), which is the result of doubling of point P.
λ = (3x12)/(2y1)
x3 = λ2 - 2x1
y3 = λ(x1 - x3) - y1
Repace point P coordinates (x1, y1) with ( x, y ) to indicate it can be any coordinate on the curve and R coordinates (x3, y3) with (xR, yR) the equations will look like:
λ = (3x2)/(2y)
xR = λ2 - 2x
yR = λ(x - xR) - y
The last three math operations may output real numbers (ℝ).
Real numbers are numbers that can be positive or negative and have decimal places after the point.
Example: ℝ = {..., -5, -2.5, 0, 3, 6.334, ...}.
In ECC we never work with real numbers only with integers (ℤ) so there are no inaccuraties due to rounding errors.
Integers are positive numbers and have no decimal places after the point.
Example: ℤ = {0, 1, 2, 3, ...}
To make the calculations go faster a finite number of integers are to be used (Fp).
The finite field (Fp) make working with curves a completely different concept.
The curves, when graphed over a finite field, do not even resemble fig 2.
When modulo p is applied, the equations of doubling a point (ECDouble) will look like:
λ = (3x2) modinv(2y) (mod p)
xR = λ2 - 2x (mod p)
yR = λ(x - xR) - y (mod p)
Procedure to calculate x and y
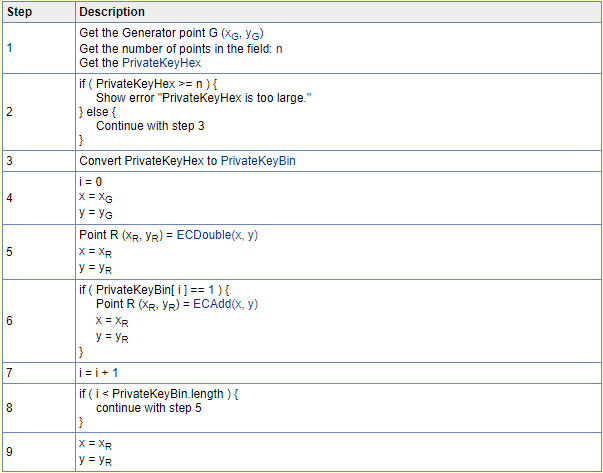
Sources:
www.secg.org
https://en.wikipedia.org/wiki/Elliptic_curve_cryptography
http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/