Comenzaremos explicando el funcionamiento de un exchange decentralizado de una simplicidad asombrosa. Cualquier persona con conocimientos básicos de smart contracts podría armarlo. Si bien el modelo más simple tendrá una utilidad limitada, explicaremos cómo mediante una pequeña sofisticación, puede lograrse una funcionalidad más completa. Allí estaremos en el caso del protocolo Bancor.
Antes de comenzar la descripción, vale la pena aclarar que nos referimos exclusivamente a exchange entre tokens contenidos en una blockchain EOS, o acaso otra blockchain que admita contratos arbitrarios y permita operar sin comisiones. Gracias al protocolo de comunicación interblockchain, también podríamos intercambiar tokens de distintas blockchains EOS. Supongamos que poseemos como ahorros una cierta cantidad x0 de un token A y otra cantidad y0 de un token B, de manera que ambas cantidades están igualmente cotizadas en el mercado. Podemos entonces crear un contrato (exchange) que aceptará tokens A para cambiar por tokens B o bien tokens B para comprar tokens A. Debemos preguntarnos qué precio debe solicitar el contrato para cambiar, de manera que los compradores estén interesados pero que al mismo tiempo el exchange no pierda sus tokens. ¿Es esto posible sin que el contrato reciba información extra del resto del mundo? Teniendo en cuenta que el protocolo Bancor lleva activo varios meses sobre Ethereum, la respuesta esperada es sí. Desde @eosargentina tomamos nota ante el anuncio de Daniel Larimer de incorporar el protocolo Bancor en el diseño de herramientas financieras para EOS. Esto nos llevó a estudiar Bancor con cierto detalle y el contenido de este artı́culo es fruto de ese estudio.
Al momento de la inicialización, sabemos que en el mercado se pueden cambiar x0 tokens A por y0 tokens B. Éste será el precio del exchange en el instante inicial. La tasa de cambio entonces será
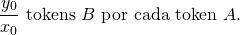
Es práctico elegir un spread igual a 0. Ahora debemos programar una tasa de cambio que dependa exclusivamente de las cantidades de tokens A y B que posee el exchange. Pero en verdad vamos a imponer que la cantidad de uno de los dos tokens presente en el exchange determina la cantidad del otro. Si así no fuera, tendríamos eventuales ganancias o pérdidas absolutas en tokens A o en tokens B que no tendrían razón de ser. Una pérdida no sería deseable, mientras que una ganancia no estaría justificada dado que aún no hemos impuesto comisiones y hemos fijado el spread en cero. Elijamos pues como variable independiente x la cantidad de tokens A presentes en el exchange. De esta forma, y(x) será la cantidad de tokens B presentes en el exchange cuando haya x tokens A. Sabemos que y(x0)= y0.
Consideremos ahora, como posibilidad, que el precio siempre esté dado por la proporción y/x y veamos a qué conduce. El precio del token B dice cómo es la variación infinitesimal de la función y. Más exactamente, el precio del token B es igual a -y' , donde y' es la derivada de la función y. Nuestra condición es, entonces, -y'=x/y. Esta ecuación diferencial conduce a la solución
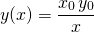
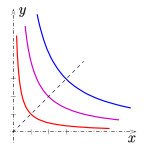
Esta función sencilla permite calcular el precio efectivo para realizar una operación. El precio instantáneo y/x en realidad no es suficiente, ya que el precio va aumentando infinitesimalmente durante la compra, por decirlo de algún modo. Sin embargo, si la operación es pequeña en comparación con la reserva del exchange, el precio y/x será una buena aproximación. Naturalmente, la función y es estrictamente decreciente: cuanto mayor sea x, menor será y. Además no es posible vaciar el exchange porque se requerirı́a infinitos tokens A para comprar todos los tokens B y viceversa. Notar que si el precio y/x difiere del precio en el mercado, habrá usuarios interesados en operar en nuestro exchange hasta equilibrar el precio. Por lo tanto el precio de nuestro exchange guardará una estrecha relación con el precio en el mundo exterior.
Hasta aquí hemos descripto el modelo más sencillo posible para un exchange automático. Es importante notar que este modelo es el que utiliza Bancor. Se puede consultar por ejemplo EOSBNT Relay y Bancor network para verificar que el precio relativo entre EOS y BNT coincide con la proporción entre las reservas, salvo por la comisión que surge de operar en Ethereum. La diferencia entre nuestro exchange y el ejemplo de Bancor, es que éste admite ingreso y egreso de capital (tokens EOS y BNT) mediante un token auxiliar, EOSBNT. Sobre este punto tal vez podamos entrar más en detalles en un artı́culo próximo. La ventaja reside en la unificación, distintos capitales pueden participar en un mismo exchange.
Una pregunta fundamental es: ¿se puede garantizar que el exchange no pierde dinero? Por supuesto, si los tokens A y B se desvalorizan, el exchange perderá dinero: los milagros no existen (los almuerzos gratis a veces sí...). Si analizamos las reservas en cualquier instante, encontramos que al medirlas en tokens B, tenemos y + xy/x = 2y, o bien medidas en tokens A, x + yx/y = 2x. Dado que y es decreciente, para todo x distinto de x0 tendremos que x > x0 e y < y0 o bien x < x0 e y > y0. Es decir que la capitalización del exchange mejoró midiendo en uno de los tokens pero empeoró midiendo según el otro. Hasta aquí no es claro que nuestro exchange no pierde dinero. Debemos refinar el análisis. Supongamos que luego de cierto tiempo, el exchange se halla en el estado (x, y). Sean pA y pB los precios de los tokens A y B medidos en alguna referencia externa considerada estable. Podemos preguntarnos qué estado es más valioso, si (x, y) o (x0, y0). Es decir, el estado actual, o el capital que teníamos inicialmente.
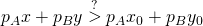
Podemos dividir ambos miembros por pB, y usar que pA/pB es el precio relativo entre A y B, es decir que es igual a y/x. Luego de reemplazar y = x0 y0/x llegamos a que la anterior desigualdad es equivalente a
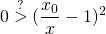
que es obviamente falsa. La conclusión es que el exchange siempre pierde a medida que el precio relativo entre A y B se aleja del inicial. Esto resulta sorprendente, porque ahora es difícil explicar el incentivo que existe para depositar capitales en sistemas actualmente utlizados. No intentaremos aquí responder a esa pregunta. Consideremos en cambio la opción de incluir una comisión para operar. Dada la naturaleza oscilante de los mercados, una muy pequeña comisión debería bastar para restituir el incentivo. Este modelo permite visualizar lo fácil que será en un futuro invertir en el mercado cambiario, proveyendo liquidez a cambio de una cierta rentabilidad esperada.