Online social networks have become a staging ground for modern societal movements. The Arab Spring, for example, is widely considered the most prominent example with 90% of Egyptians and Tunisians indicating that they used Facebook to organize protests and spread awareness. As a precautionary measure, governments have taken to blocking social networking websites, showcasing the importance of understanding this phenomenon. Characterizing information diffusion on social platforms like Twitter enables us to understand the properties of underlying media and model communication patterns.1 We can use epidemiological models to describe the rate at which information spreads. Specifically, we use the SEIZ epidemic model to describe the spread of a fake AP News tweet in 2013. With our model we hope to show how dangerously fast a rumor from an accredited news source can spread.2 In this project we hope to be able to estimate parameter values by sculpting our model around our Infected data and suggest an improved model to describe the spread of rumors on social media.
The Model
In the context of Twitter, the different compartments of the SEIZ model can be viewed as followed: Susceptible (S) represents a Twitter user who is unaware of the rumor. Infected (I) denotes a user who has tweeted about the rumor. Skeptic (Z) is a user who is aware of the rumor but chooses not to tweet about it. Lastly, Exposed (E) represents a user who has seen the rumor via a tweet, but has taken some time — an exposure delay — prior to posting. Our model is represented in Figure 1 below:

The SEIZ rules can be summarized as follows:
• Skeptics come into contact with a susceptible at rate b. These interactions may result in either turning the individual into another skeptic at probability l, or turning that person into an exposed individual at probability (1 − l).
• Infected individuals come into contact with a susceptible at rate β. These interactions may result in the individual believing the rumor and moving to the Infected I compartment at probability p, or moving to the exposed E compartment with probability (1 − p).
• Transitioning of individuals from the exposed E compartment to the infected class can be the result of one of two separate mechanisms: (i) an exposed individual has further contact with an infected individual at rate ρ, or (ii) an exposed individual may become infected by self adoption with rate ϵ.
Our differential equations describing our model are as followed:
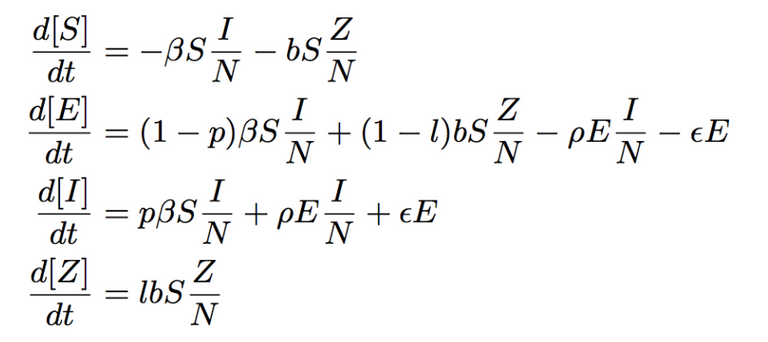
There are few available resources to retrieve data regarding online social interactions. Because of a lack of available data, the transition rates between the compartments and the exact initial sizes of the compartments are constructed through estimation that is strictly based off of what we saw on Twitter and the available statistics we could find.
Assumptions
For our model, we assume the following in our SEIZ model implementation:
• Infected individuals, I, submit a tweet.
• Skeptics, Z, believe the rumor to be false, but do not tweet.
• N is a constant.
• Once an individual is in either I or Z they cannot move elsewhere.
The Rumor
On April 23rd, 2013, at 1:08 PM a fake tweet appeared on the AP Twitter account (@AP), which had more than 1.9 million followers: "Breaking: Two Explosions in the White House and Barack Obama is injured.” - The tweet was deleted within two minutes. Only 12% of the account’s followers might have read this on their timeline.5 Using this, we estimate the total population, N, to be 226,000 individuals. Furthermore, we counted a total of 791 tweets about this rumor in the time span between 1:08 PM and 1:10 PM, thus we expect I not to increase above 791 in our model.

Results & Analysis
Initially, we assumed that there would be a time delay from when the tweet was posted to when people became infected. We also assumed a high probability p of becoming an infected tweeter, a low probability l of becoming a skeptic , and a high contact rate ρ between the exposed and infected. Finally we assumed that at t0, S→I (β) and S→Z (b) contact rates would be the same. Figure 3 shows our expected graph:

Figure 3 describes an initial period of about 16 seconds before the rumor began to spread. At t=20, we see a rapid increase in the number of people exposed to the rumor, peaking at 30 seconds with 140,065 people in the E compartment. Meanwhile, the number of people tweeting about the rumor approaches and is asymptotic to N as t approaches 120 seconds.
However, this is not what our dataset shows us. Our data does indicate a similar initial time-delay before the rumor starts to spread, but the number of infected users does not increase above 791. For our adjusted model, we increased the initial number of skeptics to 80,000, causing the contact rate to increase also. Furthermore, we increased probability of becoming a skeptic, l, to 0.698. Lastly we decreased the contact rate β to 0.04, as there are more skeptics than infected individuals initially. This gave us a RSS value of 3066.866, of the I-data to the I-curve. Shown in Figure 4.
We then compared the SEIZ model to a simple SIS model with differential equations:
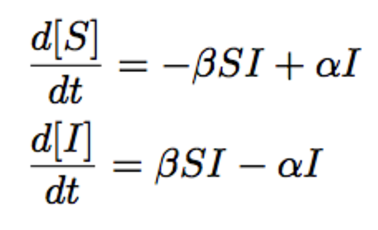
Figure 5 shows the SIS Infected curve and the Infected data.
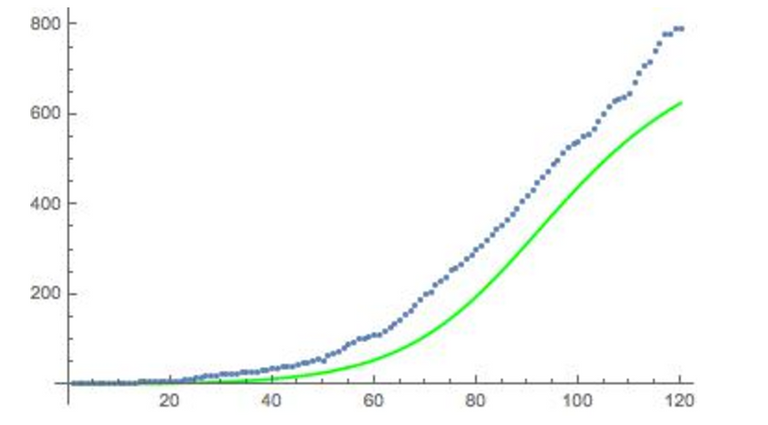
We used the same value for β, 0.04, and varied α until we achieved the lowest RSS value of 5888.34 and AICc of 207.54.
Finally, we used the Akaike Information Criterion (AICc) to understand which model was of better quality. The SEIZ model has both the lowest RSS value of 3066.866 and AICc value of 181.64. Other researchers have come to the same conclusion that the SEIZ model is a better model than the SIS model.
Conclusion
We have demonstrated how quickly a rumor from an accredited news source can propagate over Twitter through epidemiologically-based population models. We have shown that by sculpting the model to fit the I data, the SEIZ model can capture the spread of a rumor accurately, thereby generating a wealth of valuable parameters to facilitate the analysis of these events.
Although there is no such “immune system” in our model, we want to suggest an improvement to our model that does incorporate an “immune response”. In this new model, the Skeptics do tweet and therefore they would be able to convince Exposed and Infected individuals that the rumor is not true, and conversely the Infected individuals can convince the skeptics of the truth of the rumor. Building on this new model, we would include time dependent parameters. By using this new model we would be able to not only further understand how a rumor can spread but observe the rate at which the parameter values change. This could give us insight as to whether a rumor or news story is true.
This is the final project for a math modeling class myself and my friend Mike took in the fall. I'd be very interested in doing something similar with how an idea or rumor might spread on Steemit.
References
[1] Fang Jin,, Edward Dougherty, Parang Saraf , Yang Cao, Naren Ramakrishnan. Epidemiological Modeling of News and Rumors on Twitter. Department of Computer Science, Genetics, Bioinformatics, and Computational Biology Department Virginia Tech.
[2] L. Bettencourt, A. Cintron-Arias, D. I. Kaiser, and C. Castillo-Chavez. The power of a good idea: Quantitative modeling of the spread of ideas from epidemiological models. PHYSICA A, 364:513–536, 2006.
[3]M. Cha, H. Haddadi, F. Benevenuto, and K. P. Gummadi. Measuring user influence in twitter: The million follower fallacy. 2010.
[4]D. J. Daley and D. G. Kendall. Epidemics and rumours. Nature, 204, 1964.
[5] https://www.statista.com/topics/737/twitter/
neat AF, teddy!
Cheers Ned!