The Moment of Inertia of a Rotating Object Depends on the length of the Radius And The mass of the load

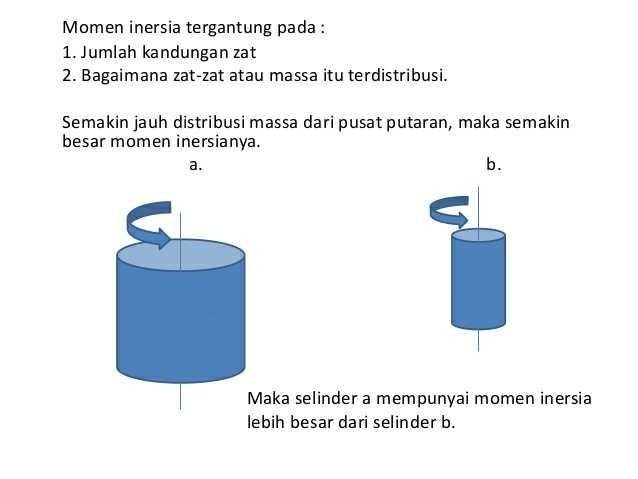
source jpg . https://www.google.co.id/search?q=bergantung+pada+apa+momen+inersia&client=ucweb-b&channel=sb&biw=360&bih=523&tbm=isch&ei=_EexWuvsCMii0gSDm4_YBw&start=40&sa=N#mhpiv=9&spf=1521567751494
The moment of inertia (SI unit: kg m2) is the measure of the inertia of an object to rotate against its axis. This magnitude is the rotational analogue of the mass. The moment of inertia plays a role in the dynamics of rotation like mass in basic dynamics, and determines the relationship between angular momentum and angular velocity, force moment and angular acceleration, and several other quantities. Despite the scalar discussion of the moment of inertia, the discussion using the tensor approach allows for more complicated system analysis such as gyroscopic movement.
Symbols and sometimes also commonly used to refer to moments of inertia.
This concept was introduced by Euler in his book Theoria motus corporum solidorum seu rigidorum in 1730. [1] In the book, he discusses moments of inertia and many related concepts.
The simple definition of the moment of inertia (against the particular axis of rotation) of any object, either the point mass or the three-dimensional structure, is given by the formula:
where m is mass and r is the distance perpendicular to the axis of rotation.
Analysis
The moment of inertia (scalar) a point mass that rotates on a known axis is defined by
The moment of inertia is an additive. Thus, for a rigid body composed of N the mass of the mi point with a ri spacing of the rotation axis, the total inertia moment equals the sum of the inertia moments of all point mass:
For solid objects described by the mass density function ρ (r), the moment of inertia of a given axis can be calculated by integrating the square of the distance against the rotational axis, multiplied by the mass density at a point in the object:
Where
V is the volume occupied by object ρ is the spatial density function of object = (r, θ, φ), (x, y, z), or (r, θ, z) is the vector (perpendicular to the rotation axis) between the axis of rotation and the point at the object. Diagram of the moment calculation of the inertia of a disc. Here k is 1/2 and is the radius used to determine the moment of inertia
Based on dimensional analysis only, the moment of inertia of an object not a point must take the form:
Where
M is the mass R is the object's radius of the center of mass (in some cases, the length of the object used) k is the dimensionless constant called the "inertia constant", which varies depending on the corresponding object.
The inertia constant is used to calculate the difference in the location of the mass from the center of the rotation. Example:
k = 1, thin ring or thin cylinder around center = 2/5, solid ball around center = 1/2, cylinder or solid disk around the center.