Amazingly, two strangers communicating over an insecure channel can create shared secrets only they know. One way is using the Elliptic Curve Diffie Hellman algorithm. Ethereum Classic (ETC) network nodes use this algorithm to create shared secrets for encryption and authentication.

Basics

ETC nodes are distinguished by Elliptic Curve Digital Signature Algorithm (ECDSA) public keys. These public keys are derived from random numbers, referred to as private keys, by an odd type of multiplication involving number pairs.

If node A wants to establish a shared secret with node B, node A generates new private and public keys. The new public key is sent to node B. The shared secret will be the result of multiplying the new private key and the public key of node B. Node B can also determine the shared secret by multiplying its private key and the received public key. Each calculation will produce the same results! A shared secret is then securely established despite the communication channel potentially being insecure.

As an analogy, consider Alice and Bob trying to establish a shared secret paint color. Both mix a random color with yellow paint and share the resulting mixture. Each then combines their received mixture with their random color:

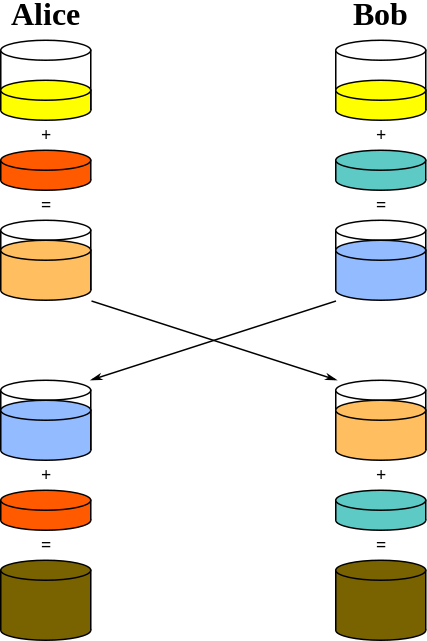
Alice and Bob both end up with the same color! Furthermore, assuming it is infeasible to isolate the contents, analyzing the mixtures does not reveal the final color. The random colors correspond to private keys. The mixtures correspond to public keys. The final color corresponds to the shared secret.

Implementation

Here is Python code ETC nodes could use to establish a shared secret.

#!/usr/bin/env python3

import random

N  = 115792089237316195423570985008687907852837564279074904382605163141518161494337
P  = 115792089237316195423570985008687907853269984665640564039457584007908834671663
Gx = 55066263022277343669578718895168534326250603453777594175500187360389116729240
Gy = 32670510020758816978083085130507043184471273380659243275938904335757337482424

def invert(number, modulus):
        """
        Finds the inverses of natural numbers.
        """

        result = 1
        power  = number
        for e in bin(modulus - 2)[2:][::-1]:
                if int(e):
                        result = (result * power) % modulus
                power = (power ** 2) % modulus

        return result

def add(pair_1, pair_2):
        """
        Finds the sums of two pairs of natural numbers.
        """

        if   pair_1 == [0, 0]:
                result = pair_2
        elif pair_2 == [0, 0]:
                result = pair_1
        else:
                if pair_1 == pair_2:
                        temp = 3 * pair_1[0] ** 2
                        temp = (temp * invert(2 * pair_1[1], P)) % P
                else:
                        temp = pair_2[1] - pair_1[1]
                        temp = (temp * invert(pair_2[0] - pair_1[0], P)) % P
                result = (temp ** 2 - pair_1[0]  - pair_2[0]) % P
                result = [result, (temp * (pair_1[0] - result) - pair_1[1]) % P]

        return result

def multiply(number, pair):
        """
        Finds the products of natural numbers and pairs of natural numbers.
        """

        result = [0, 0]
        power  = pair[:]
        for e in bin(number)[2:][::-1]:
                if int(e):
                        result = add(result, power)
                power = add(power, power)

        return result

def make_private_key():
        """
        Creates random private keys.
        """

        return random.randint(1, N)

def get_public_key(private_key):
        """
        Calculates public keys from private keys.
        """

        return multiply(private_key, (Gx, Gy))

def get_shared_secret(private_key, public_key):
        """
        Calculates shared secrets from public and private keys.
        """

        return multiply(private_key, public_key)

Example

Here is a sample session in a Python shell:

>>> private_key_1 = make_private_key()

>>> private_key_1
97213711440252288069501705296405261088977963748356197430111018664708007898694

>>> public_key_1 = get_public_key(private_key_1)

>>> public_key_1
[55347035383335640130848668571903826856724561960411750372299562338900707959329, 56987405272845225816494709602265870995367253030969066517972976881897442374061]

>>> private_key_2 = make_private_key()

>>> private_key_2
114442312191143111200801983145915249881179214150404268170023204631602354988735

>>> public_key_2  = get_public_key(private_key_2)

>>> public_key_2
[46199435999571260839088012456481977088200767000880651780506032156594168787887, 42363090186990936702404058277398340643564495339378028219129719226661858237092]

>>> get_shared_secret(private_key_1, public_key_2)
[44866827294122005264365746646122394461069726466915377589895810140980695289009, 62851244191510099945744865372108107629218872326463084894219243426735245634939]

>>> get_shared_secret(private_key_2, public_key_1)
[44866827294122005264365746646122394461069726466915377589895810140980695289009, 62851244191510099945744865372108107629218872326463084894219243426735245634939]