L'intelligence artificielle peut être utilisée pour répondre à des problématiques majeurs. Cette technologie peut nous aider dans nos analyses et peut nous permettre de prendre de meilleurs décisions. C'est notamment le cas dans le domaine médical. Dans cet article, nous allons nous intéresser aux maladies cardiaques. Pour cette étude, nous allons utiliser les données présentes sur Kaggle. Nous vous invitons aussi à suivre cette étude en utilisant le kernel que nous vous avons mis à disposition sur Kaggle regroupant l'ensemble des codes utilisés. Ce dernier étant fonctionnel, vous pourrez suivre les différentes étapes que nous avons réalisées. De plus, cela vous permettra de réaliser différents tests ou de poursuivre cette étude de votre côté.
Présentation du problème
Nous avons à notre disposition une base de données de personnes avec différentes caractéristiques. À partir de ces données, nous allons chercher à déterminer si la personne est atteinte d'une maladie cardiaque ou non. Ainsi, cela permettrait de faciliter la tâche d'un médecin. On pourrait imaginer par la suite automatiser la partie analyse afin d'accélérer les résultats et la prise en charge du patient.
Notre base de données
Nous avons à notre disposition une base de données contenant 14 attributs jugés intéressants. En effet, une base de données plus conséquente en attributs est accessible. Cette dernière en possède 76. Cependant, nous allons chercher à minimiser le nombre d'attributs afin de simplifier le coût de notre démarche. En effet, pour chacun des attributs, nous devons effectuer une mesure sur le patient. Le fait de réduire ce nombre, nous permet de réaliser un traitement plus rapide, car nous avons moins de mesures à prendre. Cependant, le fait de prendre moins d'attributs en compte peut poser problème. En effet, les erreurs de mesures peuvent arriver et ainsi provoquer de mauvaises prédictions. Généralement, chaque valeur est réalisée à partir d'un échantillon prélevé. Ainsi, les erreurs ne devraient pas être répercutées sur les autres valeurs à part si nous avons une erreur lors de la prise de l'échantillon mère.
Présentation des données
Durant cette étude, nous allons utiliser la base de données contenant 14 attributs. Les informations que nous allons avoir sont : l'âge, le sexe, le type de douleur thoracique, la tension artérielle au repos, le taux de cholestérol sérique en mg/dl, la glycémie à jeun > 120 mg/dl, les résultats électrocardiographiques au repos, la fréquence cardiaque maximale atteinte, la présence d'une angine de poitrine induite par l'exercice, la présence d'un ST dépression induite par l'exercice par rapport au repos, la pente du segment ST d'exercice de pointe, le nombre de vaisseaux principaux colorés par la fluorescence, le niveau de Thalassémie et le résultat du diagnostic.
Nous allons visualiser un échantillon de données afin de comprendre un peu mieux nos données :
data = pd.read_csv('../input/heart.csv')
data.head()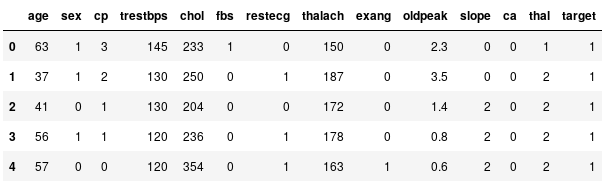
Échantillon de données
Ici, nous pouvons constater que certaines variables correspondent à des valeurs booléennes, à des catégories ou à des valeurs numériques. Ainsi, il va nous falloir traiter ces éléments différemment en fonction de leur type.
Analyse et traitement des variables
Dans cette partie, nous allons chercher à analyser nos données et à les modifier afin de permettre une meilleure analyse. Il est à noter que nous n'avons pas de valeurs manquantes dans nos données.
La variable âge
Nous allons dans un premier temps analyser la répartition de nos valeurs pour l'attribut âge.
import seaborn as sns
import pandas as pd
g = sns.kdeplot(data["age"][(data["target"] == 0) & (data["age"].notnull())], color="Red", shade = True)
g = sns.kdeplot(data["age"][(data["target"] == 1) & (data["age"].notnull())], ax =g, color="Blue", shade= True)
g.set_xlabel("Age")
g.set_ylabel("Frequency")
g = g.legend(["Malade","None"])
Densité des personnes malades ou non en fonction de leur âge.
Comme vous pouvez le constater, nous avons des données avec un âge compris entre 20 et 80 ans. De plus, nous pouvons constater une densité plus importante pour les personnes malades âgées de 60 ans. Cet écart d'âge peut parfois être problématique pour notre modèle. Ainsi, nous allons chercher à normaliser l'âge. Plusieurs possibilités s'offrent à nous dont la normalisation min-max et la normalisation par Z-score
Normalisation min-max
La première solution est de se baser sur le minimum et le maximum de nos données. Nous nous basons sur les bornes de notre intervalle.
Normalisation score-z
La seconde solution est de nous baser sur la moyenne et l'écart-type de nos données. Ainsi, nous nous approchons d'une loi normale centré-réduite.
Notre choix de normalisation
Notre choix s'est porté sur la dernière normalisation. Ainsi, pour la coder, nous faisons :
average = data["age"].mean()
std = data["age"].std()
data["age"] = (data["age"] - average) / stdAinsi, cette normalisation change les valeurs de nos données en les concentrant. Nous obtenons ainsi une moyenne de 0. Cependant, nous conservons la répartition de nos données. Nous pouvons visualiser cela à l'aide de la figure ci-dessous :
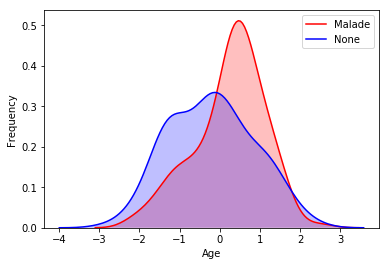
Densité normalisée des personnes malades ou non en fonction de leur âge.
La variable chest pain type (cp)
Nous allons maintenant nous intéresser au cas à la variable concernant le type de douleur thoracique d'une personne. Nous allons, dans un premier temps, regarder les différentes valeurs possibles pour cette variable, mais aussi le nombre d'éléments présents pour chacun d'entre elles.
data["cp"].value_counts()0 143 2 87 1 50 3 23 Name: cp, dtype: int64
Comme vous pouvez le constater, nous avons à notre disposition quatre valeurs différentes, chacune représentant un type de douleurs. Lorsque nous avons une variable qui fait référence à plusieurs catégories, nous encodons cette variable en utilisant, généralement, un encodage one-hot (One Hot Encoding).
Encodage One-Hot - One Hot Encoding
L'encodage One-Hot à pour objectif d'encoder notre valeur sous format binaire (0 ou 1). Ainsi, chaque nombre représente une catégorie. Par exemple, si nous prenons le cas de la variable sur le type de douleur thoracique et que nous l'encodons sous le format One-Hot, nous allons avoir 4 valeurs binaires représentant chacune les 4 catégories différentes présentent dans notre jeu de données. Afin d'exprimer la présence d'une des catégories, nous allons utiliser la valeur 1, et le reste sera des 0.
La particularité de cet encodage et qu'elle nous permet de simplifier l'expression de notre variable à notre machine. De plus, elle permet d'éviter différents problèmes lors de l'apprentissage. En effet, lors de l'apprentissage, un modèle peut penser que si des catégories ont des valeurs numériques, relativement proches (catégorie 1, catégorie 2), il sera amené à penser qu'elles sont peut-être liée. Or, cela peut ne pas être le cas. Pour cela, le format One-Hot permet de définir la présence ou non d'une catégorie sans pour autant influencer notre modèle.
Enfin, le format d'encodage One-Hot peut parfois être compliqué à mettre en place, notamment dans le cas ou nous avons énormément de catégories. En effet, pour une variable ayant 4 valeurs différentes, nous avons eu 4 nouvelles variables. Or, si nous avons une variable qui possède 100 valeurs différentes, alors nous aurons 100 nouvelles variables. Comme vous pouvez le constater, plus il y a de diversité dans nos données et plus la représentation sous le format One-Hot est compliqué à mettre en place.
Les autres variables
Dans cette étude, nous avons deux manières de transformer notre information. La première en utilisant le Z-score et la seconde en utilisant un encodage One-Hot. Pour ce qui est des autres variables, nous avons décidé d'appliquer ces deux transformations. Bien entendu, d'autres possibilités sont possibles.
Ainsi, nous allons utilisé le Z-score pour les variables liées à l'âge, à la tension artérielle au repos, au cholestérol sérique, à la fréquence cardiaque maximale atteinte et à la pente du segment ST d'exercice de pointe. Pour les autres variables présentes, nous allons utiliser l'encodage One-Hot.
Création d'un système fonctionnel
Afin de réaliser notre système, nous allons devoir, dans un premier temps, réaliser la préparation de nos données en utilisant les différents procédés énoncés précédemment. Ensuite, nous allons devoir sélectionner un classificateur qui soit performant sur notre cas d'étude.
Transformation de nos données
Nous allons dans cette partie, réaliser une pipeline réalisant les différentes transformations sur nos données.
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.pipeline import FeatureUnion
class DataFrameSelector(BaseEstimator, TransformerMixin):
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, X, y=None):
return self
def transform(self, X):
return X[self.attribute_names]
num_pipeline = Pipeline([
("select_numeric", DataFrameSelector(["sex", "fbs", "exang", "cp", "restecg", "slope", "ca", "thal"])),
("cat_encoder", OneHotEncoder(sparse=False, categories='auto')),
])
standard_pipeline = Pipeline([
("select_numeric", DataFrameSelector(["age", "trestbps", "chol", "thalach", "oldpeak"])),
('scale', StandardScaler()),
])
preprocess_pipeline = FeatureUnion(transformer_list=[
("num_pipeline", num_pipeline),
("standard_pipeline", standard_pipeline),
])
Une fois notre pipeline réalisée, il ne nous reste plus qu'à donner en entrée de celle-ci nos données. Pour ce faire, nous allons, dans un premier temps, mettre de côté la variable indiquant le résultat du diagnostic, car c'est ce que l'on cherche à prédire. Une fois nos données transformées, il ne nous reste plus qu'à séparer notre jeu de données en deux : une partie pour la phase d'entraînement et une autre pour la phase de test.
from sklearn.model_selection import train_test_split
target = data["target"]
data.drop('target', axis=1, inplace=True)
data = preprocess_pipeline.fit_transform(data)
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.20, random_state=42)Réalisation de différents modèles
Dans cette étude, nous allons utiliser trois modèles dont un système de forêt d'arbres de décisions (Random Forest), un système de machine à vecteurs de support (Support-Vector Machine) et un système des K plus proches voisins (K-nearest neighbors).
Lors de l'analyse de ces systèmes, nous chercherons à obtenir un système performant, mais une attention particulière sera apportée sur le rappel. En effet, nous préférons que notre système nous détermine l'ensemble des personnes atteintes même si parmi elles, il y en a qui ne le sont pas. En effet, si une personne atteinte n'est pas prise en charge, cela peut avoir des répercussion graves comme retarder sa prise en charge et donc empirer la situation du patient.
Arbres de décisions - Random forest
Nous allons, dans un premier temps, utiliser un système d'arbres de décisions. Pour ce faire, en python, nous faisons :
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
forest_clf = RandomForestClassifier(n_estimators=100, max_depth=5)
forest_scores = cross_val_score(forest_clf, X_train, y_train, cv=10)
forest_scores.mean()
Pour ce qui est des hyper-paramètres utilisés, nous avons utilisé 100 arbres de décisions (n_estimators) ayant une profondeur maximum de 5 (max_depth). Puis, nous avons réalisé une validation croisée afin de vérifier notre modèle. Pour ce faire, nous réalisons la moyenne de chacun des modèles et nous obtenons un score d'environ 0.83. Comme énoncé au début de cette partie, nous allons nous intéresser au score du rappel.
from sklearn.metrics import precision_score
print ("Précision")
print(precision_score(y_test, y_pred, average='macro'))
from sklearn.metrics import recall_score
print ("Rappel")
print(recall_score(y_test, y_pred, average='macro'))
Nous obtenons pour le modèle Random Forest, une précision de 0.88 et un rappel de 0.88. Nous allons maintenant nous intéresser à la matrice de confusion de notre système qui nous permet de visualiser nos résultats.

Matrice de confusion non normalisée sur le système Random Forest.
La catégorie qui nous intéresse le plus ici est la catégorie malade. Nous pouvons remarquer qu'il y a trois personnes appartenant à la catégorie malade qui on été classifier comme étant saine. Nous avons plutôt un bon score de rappel.
Machine à Vecteurs de Support - Support-Vector Machine
Nous allons maintenant utiliser un système de machine à vecteurs de support.
from sklearn.svm import SVC
svm_clf = SVC(gamma="auto")
svm_clf.fit(X_train, y_train)
svm_scores = cross_val_score(svm_clf, X_train, y_train, cv=10)
print(svm_scores.mean())
svm_clf.fit(X_train, y_train)
y_pred = svm_clf.predict(X_test)
print ("Précision")
print(precision_score(y_test, y_pred, average='macro'))
print ("Rappel")
print(recall_score(y_test, y_pred, average='macro'))

Matrice de confusion non-normalisée utilisant un SVM
En terme de résultat, nous obtenons un score moyen par validation croisée de 0.82. Nous obtenons une précision de 0.90 et un rappel de 0.90. Il est intéressant à noter que nous obtenons des résultats différents. En effet, ce système est plus précis sur les personnes appartenant à la catégorie saine. De plus, nous obtenons un score de rappel plus élevé que précédemment.
K plus proches voisins - K-nearest neighbors
Pour finir avec les différents systèmes de classification, nous allons utiliser le système des K plus proches voisins. Ici, nous avons comme hyper-paramètre le nombre de voisins que nous souhaitons prendre en compte afin de déterminer la catégorie d'appartenance de notre donnée. Ici, nous avons choisi une valeur de 50.
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=50)
neigh.fit(X_train, y_train)
neigh_scores = cross_val_score(neigh, X_train, y_train, cv=10)
print(neigh_scores.mean())
neigh.fit(X_train, y_train)
y_pred = neigh.predict(X_test)
print ("Précision")
print(precision_score(y_test, y_pred, average='macro'))
print ("Rappel")
print(recall_score(y_test, y_pred, average='macro'))

Matrice de confusion non-normalisée utilisant un système des K plus proches voisins.
En terme de résultats, nous obtenons un score moyen de 0.79 pour la validation croisée. Nous obtenons une précision de 0.88 et un rappel de 0.88. Nous remarquons que nous obtenons des résultats assez similaires avec notre premier classificateur, à savoir le Random Forest.
Choix du modèle
Si nous nous basons uniquement sur le score du rappel, notre choix se porte sur le SVM. En effet, ce dernier à le plus haut rappel. Cependant, en nous basant uniquement sur les matrices de confusions, nous serions tentés de prendre le système utilisant un Random Forest ou les K plus proche voisins, car ils ont réussi à mieux classifier les personnes malades. En effectuant différents tests, nous avons constaté que les résultats du Random Forest fluctuaient beaucoup, contrairement aux deux autres classificateurs. Afin de visualiser cela, nous avons réaliser des boîtes à moustache reprenant les scores des validations croisées des différents systèmes basé sur le rappel.
forest_scores = cross_val_score(forest_clf, X_train, y_train, cv=10, scoring='recall')
svm_scores = cross_val_score(svm_clf, X_train, y_train, cv=10, scoring='recall')
neigh_scores = cross_val_score(neigh, X_train, y_train, cv=10, scoring='recall')
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
plt.figure(figsize=(8, 4))
plt.plot([1]*10, svm_scores, ".")
plt.plot([2]*10, forest_scores, ".")
plt.plot([3]*10, neigh_scores, ".")
plt.boxplot([svm_scores, forest_scores, neigh_scores], labels=("SVM","Random Forest", "K Neighbors"))
plt.ylabel("Recall", fontsize=14)
plt.show()
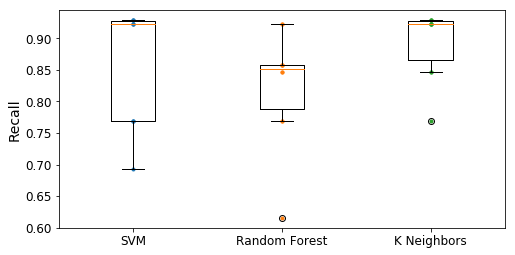
Boîtes à moustache des différents classificateurs.
Ici, nous pouvons constater que le système des K plus proches voisins est le plus stable. En effet, ces résultats sur le rappel sont très concentrés. Nous retrouvons ce phénomène pour le SVM ou la médiane est très proche du premier quartile. Cependant, ce dernier a quelques valeurs qui se dissipe. Enfin, le Random Forest possède lui aussi des valeurs qui se dissipent.
Pour ce qui est d'une mise en production, nous pouvons partir sur la mise en place d'une système implémentant les K plus proches voisins. En effet, ce dernier est relativement stable et possède de bons résultats.
Conclusion de notre problème
Dans cet article, nous avons vu comment transformer nos données en les normalisant. Cette étape est importante à réaliser, car elle permet notamment d'obtenir de bons résultats avec nos différents systèmes (les plus impactés par cela sont le SVM et les K plus proches voisins).
Puis, nous avons vu l'utilisation de plusieurs systèmes de classifications ainsi que leur analyse sur un critère, à savoir le rappel. Nous avons obtenu un système relativement performant sur ce critère. D'autres systèmes de classifications auraient pu être utilisés. De plus, dans cet article, il nous manque une phase liée à l'optimisation de notre système afin de pouvoir obtenir le meilleur système possible en production.
Pour ce qui est des possibilités de réalisation, nous pouvons tenter d'améliorer notre système tout en cherchant les variables qui ont le plus d'influence sur ce dernier. Cela pourrait être intéressant pour un médecin lors de la prise des mesures. Ainsi, il pourrait savoir qu'elle information est la plus critique pour l'analyse du système. Cela nous permettra de savoir les marges d'erreur qu'un médecin peut avoir sur la récolte des données.
J'espère que cet article vous aura plus. N'hésitez pas si vous avez des questions ou des remarques. À bientôt.
Lien original : https://www.technologieintelligente.fr/intelligence-artificielle/cas-dapplication/predire-les-maladies-cardiaques-a-l-aide-de-lintelligence-artificielle/
Processus intéressant qui pourrait grandement faciliter le travail des professionnels de la médecine. Upvoté à 100% !
Rendez-vous sur notre serveur Discord pour plus d'informationsCe post a été supporté par notre initiative de curation francophone @fr-stars.