Abstract
The full 20 week Genesis Fractal dataset is explored in detail and a model-independent method of measuring the inherent uncertainties in the consensus algorithm is presented that relies only on first principles of statistical data analysis that are well known and broadly understood.
The accuracy of the Genesis consensus algorithm is measured and characterized as indicative of a random process at work with negligible systematic error, while the precision is measured and characterized as dominated by an underlying source of systematic error that will likely remain unchanged with the addition of more weekly consensus meetings over time.
A member's attendance is shown to be a better predictor of both accuracy and precision than a member's mean Level, and it is argued that the Genesis Fractal may want to include attendance when considering future changes to their consensus algorithm.
A Genesis Uncertainty Observatory is deployed as a surveillance tool to track the accuracy and precision of the Genesis Fractal's consensus algorithm over time.
Introduction
The Genesis Fractal uses the judgment of its members to mine their community's token using a Proof of Work consensus algorithm analogous to the Bitcoin Proof of Work consensus algorithm. The fundamental difference between the two consensus algorithms is in how Proof of Work is measured and how rewards are subsequently allocated.
The purpose of this article is to focus on the measurement aspect of a Fractal's Proof of Work consensus algorithm and to describe in detail the measurement techniques available to a Fractal to characterize the quality if its measurements. The motivation of this article is to provide insight to the fractally team, the Genesis Fractal and to future Fractals on how to judge the merits of proposed changes to their consensus algorithm, such as those described in Fractally White Paper Addendum 1.
While the Bitcoin model measures Proof of Work objectively, the Fractal model measures Proof of Work subjectively. This begs the question of how one goes about characterizing the measurement quality of a Fractal's collection of subjective judgments. As with any analysis we look to first principles and use the metrics available, which for this article is the Genesis Fractal dataset. Let us begin.
The Genesis Fractal Dataset and Experimental Apparatus
In the case of the Genesis Fractal there are four relevant metrics collected on a weekly basis for each member, three of which are objective metrics and one of which is a subjective metric:
- Unique member identifier (objective metric)
- Meeting date (objective metric)
- Group identifier of a small weekly group of five or six randomly assigned members (objective metric)
- The rank order consensus opinion of the recent relative value contributed to the Fractal by the members of the small group in #3 (subjective metric)
The subjective metric from #4 is the output from the Fractal's Proof of Work consensus algorithm and is called Level. Values of Level have values that are either NULL or a unique positive integer assigned to each member by their weekly group as described in #3. If there are six members in a group then each member is assigned a Level from the set 6, 5, 4, 3, 2 and 1. If there are five members in a group then each member is assigned a Level from the set 6, 5, 4, 3 and 2. The largest value of Level, 6, is assigned to the member who made the most valuable contribution as judged by the consensus opinion of their small group. The member who was judged with the next most valuable contribution is assigned the Level 5, and so on. If a group fails to reach consensus then each member is assigned a Level of NULL for that week.
Although not the subject of this article, each member's weekly Level is proportional to a weekly reward, which is analogous to Bitcoin's Proof of Work BTC reward. This reward is the economic incentive that creates member loyalty and keeps the Fractal intact. Suffice it to say that there are no known instances of a group failing to reach consensus where each member is assigned a Level of NULL for that week.
Membership in the Genesis Fractal is open to the general public who meet these two requirements:
- They speak English
- They comment "I agree" on the Genesis Fractal Contributor Agreement (which requires a Hive blog account)
During a regularly scheduled weekly online meeting the members in attendance are randomly assigned to a new group (#3 in the list). This randomization process serves two purposes:
- It minimizes opportunities for members to collude, which creates trust in the Fractal Governance process.
- It maximizes the quality of the
Levelmeasurements by minimizing the measurement uncertainty. More on this in the next section.
Each weekly consensus meeting has strictly enforced start and stop times and spans exactly 45 minutes. During the meeting each person is asked to briefly introduce themselves and then to answer the following three questions in three minutes or less:
- What have you done to build the technology, raise awareness and grow adoption of fractal governance, as outlined in fractally's white paper?
- Have you invited anyone to participate and did they accept?
- How did your contributions rank last week?
There is no strict enforcement that a member answer these questions within the three minute time limit, nor is there strict enforcement that the questions be answered at all. Each member's response initiates a dialog between them and their group in an attempt to measure the relative value of each others recent past contributions towards the Fractal's mission. This process is analogous to Bitcoin mining.
Questions #2 and #3 can be answered easily, objectively and verifiably. Although the listening members could in principle transform these two answers into objective metrics, this is not done in practice.
Question #1 generates a subjective metric.
Although in theory the three minute rule should consume a maximum of 18 minutes (three minutes consumed by up to six members) leaving the group with at least 27 minutes to reach consensus on unique Level assignments, in practice a free-form dynamic discussion ensues as members attempt to measure subjective value using their own judgment. This subjective measurement process is confounded by the following:
- The open-ended nature of the first question. A member is free to define for themselves what technology to build (if anything at all) and what "raise awareness" and "grow adoption" means to them and how they chose to accomplish this.
- The diverse demographics of the Genesis Fractal's members (the only requirement is spoken English):
- Professionals and non-professionals
- Retired and non-retired
- Technical and non-technical backgrounds (YouTubers and Farmers and Software Engineers and Lawyers and Pilots and Physicists and others)
- National origin and country of residence (Mexico and Russia and South Korea and United States and Uzbekistan and others)
- The random assignment of members to their group immediately before a strictly enforced 45 minute timer starts.
The transformation of any given groups's subjective opinions into an objective Level value, either NULL or a unique positive integer, allows for traditional measurement techniques to be brought to bear for subsequent data analysis. For the analysis presented in this article no attempt is made to model the subjective measurement process that produces the Level values. Instead we rely only on first principles from statistical data analysis where the properties of an unmown random distribution, namely the subjective Level measurement, are measured and characterized.
Statistical Data Analysis From First Principles
Each member is a unique measurement device, akin to a volt meter or a bathroom scale, in their role of determining the Level metric. However, unlike a volt meter or a bathroom scale, the members of a Fractal are not individually calibrated to produce reproducible measurements. Instead we simply view the Level values as random samples from an unknown distribution. This simplifying approach allows us to make well defined, well known and broadly understood statistical measurements and inferences.
From the Genesis dataset we extract a set of unique measurements where each unique measurement is a tuple of the form (MemberID, MeetingID, Group, Level). The MemberID is a member's Hive.blog account name, a unique identifying string. The MeetingID is an arbitrary positive integer that encodes the weekly meeting date. The Group is a non-unique positive integer that identifies a weekly consensus group of five or six randomly assigned members. Although Group is non-unique across the dataset, the tuple (MeetingID, GroupID) does uniquely identify a group.
At the time of this analysis there were 116 unique members that participated in at least one of the 20 weekly consensus meetings that produced a total of 687 unique measurement tuples as described in the previous paragraph.
The following table shows the 17 unique measurements made by the Genesis Fractal of the author's contributions from the 17 weekly consensus meetings that he participated in:
| MemberID | MeetingID | Group | Level |
|---|---|---|---|
| mattlangston | 2 | 7 | 5 |
| mattlangston | 3 | 1 | 3 |
| mattlangston | 4 | 3 | 4 |
| mattlangston | 5 | 5 | 3 |
| mattlangston | 6 | 3 | 2 |
| mattlangston | 7 | 3 | 4 |
| mattlangston | 8 | 1 | 3 |
| mattlangston | 9 | 3 | 3 |
| mattlangston | 10 | 5 | 4 |
| mattlangston | 12 | 1 | 5 |
| mattlangston | 13 | 2 | 6 |
| mattlangston | 14 | 6 | 6 |
| mattlangston | 15 | 6 | 6 |
| mattlangston | 16 | 2 | 5 |
| mattlangston | 17 | 4 | 3 |
| mattlangston | 18 | 2 | 5 |
| mattlangston | 19 | 5 | 6 |
Selecting the set of measurement tuples for these 17 unique (MeetingID, GroupID) pairs resulted in 44 members (which is 38% of the Genesis membership) that the author was randomly grouped with (44 includes the author himself in the count) to produce a total of 99 unique measurement tuples (or 14% of all measurement tuples).
Excluding the author himself, the author encountered 22 unique members only once, 7 members twice, 10 members three times and 4 members four times for a total of 43. Figure 1 shows this distribution of repeat member encounters with the author.
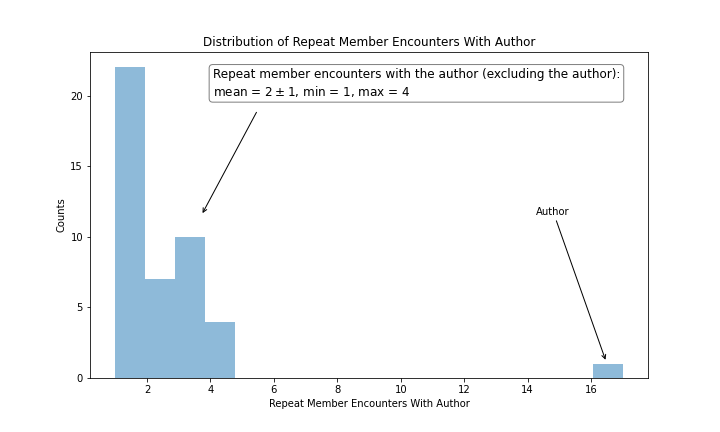 |
|---|
| Figure 1 |
The 99 unique measurement tuples where the author was the dominant measurement device are a unique sample from the full distribution. There is always only one such unique sample from the same full distribution for every member where they are the dominant measurement device. To a first approximation these samples characterize a member's accuracy (or bias) and precision (or consistency) in making subjective Level measurements for their Fractal.
The procedure to measure a member's accuracy and precision is as follows:
- Calculate the per-member statistical mean and standard deviation for the measurements from the sample where the member is the dominant measurement device. There are 44 such statistical quantities from 99 measurement tuples from the author's sample previously described.
- Calculate the per-member mean and standard deviation from a sample of all measurements from the full distribution for all members identified from step #1. There are again 44 such statistical quantities from the author's sample previously described, but a larger set of 460 measurement tuples are used to calculate these statistical quantities. This set of 460 measurement tuples includes the set of 99 from step #1, meaning that there are 361 additional unique measurement tuples contributed by the Genesis Fractal for the member's identified from step #1 where the author was not involved in the measurement process.
- Subtract the per-member statistical quantities from #1 and #2. This step requires care to ensure that uncertainties are propagated correctly through the subtraction.
- Calculate the mean and standard deviation for the statistical quantities from step #3. This step again requires care to ensure that uncertainties are propagated correctly through the mean and standard deviation operations. The mean and standard deviation are the member's
accuracyandprecision, respectively, relative to the full distribution.
This procedure produces two measures for every member, accuracy and precision. These two measures for the author are -0.20 +/- 0.19, meaning that I tend to underestimate a member's Level by -0.20 relative to other members, and am relatively consistent in doing so.
Figure 2 shows these two measures for all members sorted in ascending order along the x-axis to better highlight the range of values of the full membership. The member accuracies are shown as points and the member precisions are shown as vertical lines. The figure overlays two sets of measures where step #2 is calculated by either including or excluding the dominant member in their sample. There is no justification for removing the dominant member from their sample, but it is nonetheless shown for completeness. All subsequent discussion will refer to measurements that include the dominant member in their sample, and are labeled Include Self Measurement: True.
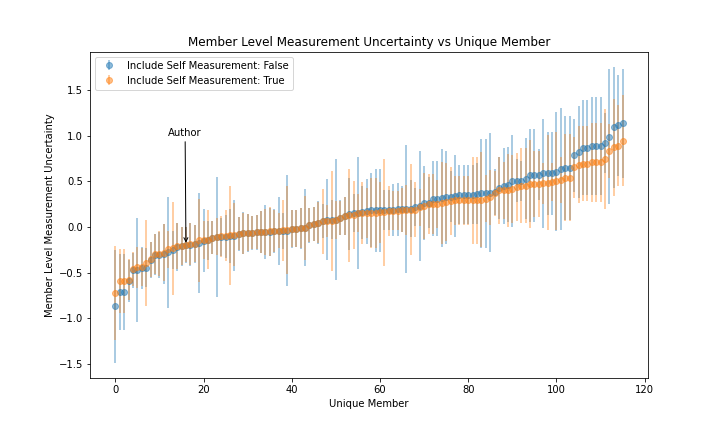 |
|---|
| Figure 2 |
Discussion
Figure 3 and figure 4 show the distributions of the same data from figure 2 where the values are simply projected onto the y-axis. A normal distribution is fit to each histogram for subsequent discussion of randomness, statistical error and systematic error.
Figure 3 shows that a normal distribution fit to the distribution of accuracy is 0.14 +/- 0.34 with a confidence level of over 99%, which is consistent with 0. This demonstrates that the Genesis Fractal is generally unbiased in its measurement of Level. Such a high confidence level (i.e. low chi-square) for data distributed according to a normal distribution is indicative of a random process at work with negligible systematic error.
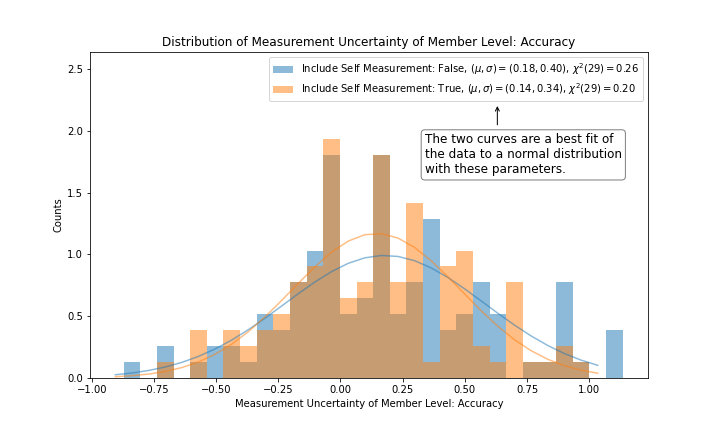 |
|---|
| Figure 3 |
Figure 4 on the other hand is a different story. A normal distribution fit to the distribution of precision yields 0.32 +/- 0.11 with a confidence level of less than 10%. The hypothesis that the Genesis Fractal's precision is due to statistical error is rejected, and we instead conclude that there is an underlying source of systematic error at work. This demonstrates that the Genesis Fractal's precision measurement of Level will likely remain unchanged with the addition of more measurements over time.
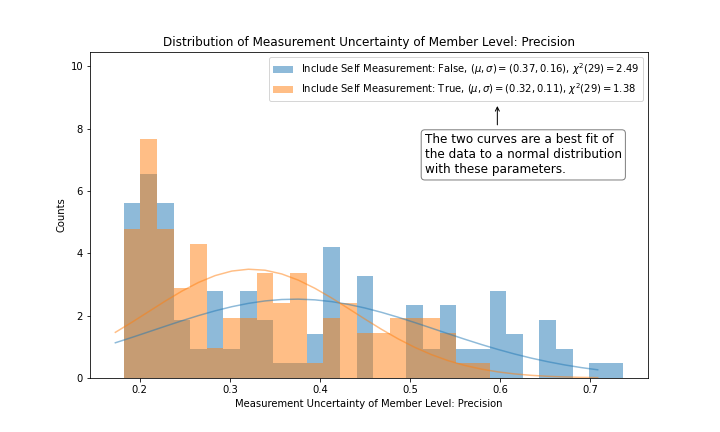 |
|---|
| Figure 4 |
The Genesis Fractal will likely need to modify their experimental apparatus to affect a change in their precision measurement of Level. This is no simple task since the source of the systematic error is unknown. The consensus algorithm and/or the measurement devices (i.e. each member's weekly consensus opinion of Level) will likely need to change to affect precision.
Correlation of Accuracy and Precision with Other Observables
In this section we investigate the correlation of accuracy and precision with other measured observables from the Genesis Fractal dataset.
Figure 5 and figure 6 show the correlation of the per-member accuracy and precision with each member's mean Level. The correlation coefficient is -0.37 for accuracy and -0.41 for precision. While this supports the belief that members assigned higher values of Level generally have better accuracy and precision, it is worth noting that members with the highest mean Level of 6 perform more poorly than members with a mean Level of 4 and 5 in terms of accuracy and more poorly than members with a mean Level of 3, 4 and 5 in terms of precision.
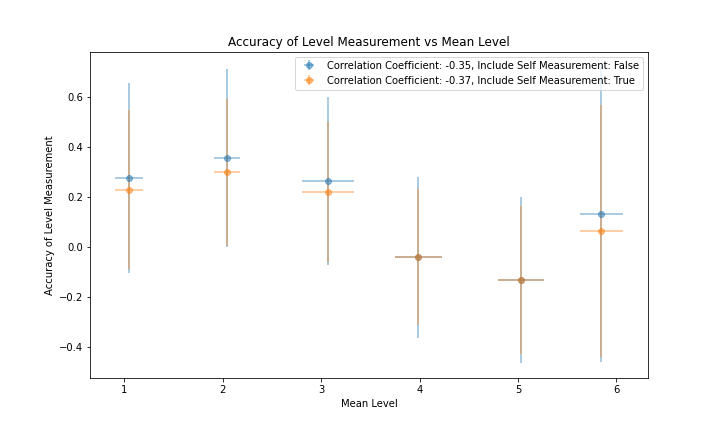 |
|---|
| Figure 5 |
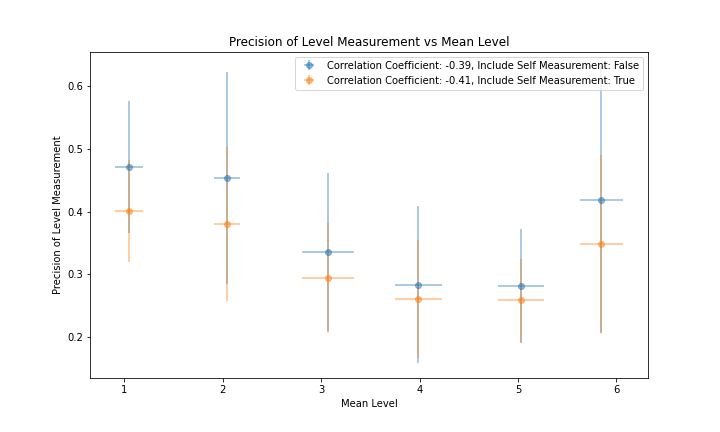 |
|---|
| Figure 6 |
Figure 7 and figure 8 show the correlation of the per-member accuracy and precision with each member's attendance record. The correlation coefficient is -0.46 for accuracy and -0.77 for precision. These stronger correlations demonstrate that attendance is a better predictor of both accuracy and precision than a member's mean Level, and that the Genesis Fractal may want to include attendance when considering future changes to their consensus algorithm.
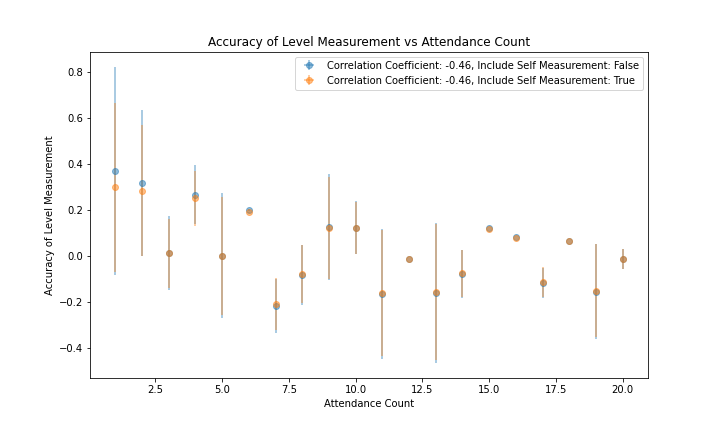 |
|---|
| Figure 7 |
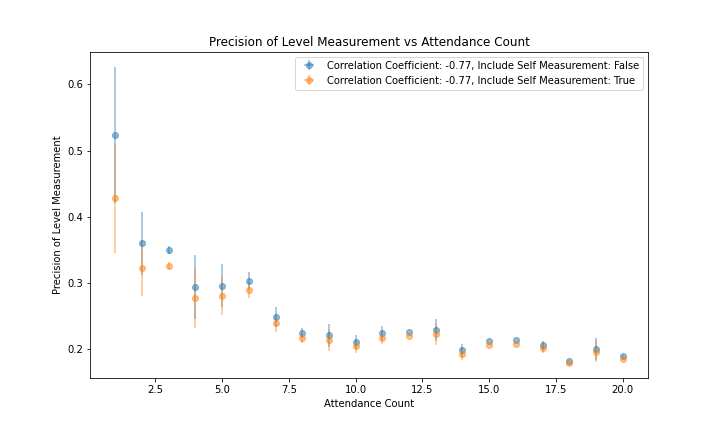 |
|---|
| Figure 8 |
Conclusion
The Genesis Fractal's experimental apparatus was reviewed and the consensus algorithm described. The full 20 week Genesis dataset was explored in detail and a model-independent method of measuring the inherent uncertainties in the consensus algorithm was presented that relies only on first principles of statistical data analysis that are well known and broadly understood.
The accuracy of the Genesis consensus algorithm was measured to be 0.14 +/- 0.34 with a confidence level of over 99%, which is indicative of a random process at work with negligible systematic error.
The precision of the Genesis consensus algorithm was measured to be 0.32 +/- 0.11 with a confidence level of less than 10%, which is indicative of an underlying source of systematic error. This precision will likely remain unchanged with the addition of more measurements over time.
The correlation of accuracy and precision with other observables from the Genesis dataset was also explored.
The correlation of the per-member accuracy and precision with each member's mean Level was measured to be -0.37 for accuracy and -0.41 for precision. While this supports the belief that members with higher average values of Level generally have better accuracy and precision, it was noted that members with the highest average Level of 6 perform more poorly than members with an average Level of 4 and 5 in terms of accuracy and more poorly than members with an average Level of 3, 4 and 5 in terms of precision.
The correlation of the per-member accuracy and precision with each member's attendance record was measured to be -0.46 for accuracy and -0.77 for precision. These stronger correlations demonstrate that attendance is a better predictor of both accuracy and precision than a member's mean Level. It was noted that the Genesis Fractal may want to include attendance when considering future changes to their consensus algorithm.
A Genesis Uncertainty Observatory is deployed as a surveillance tool to track the accuracy and precision of the Genesis Fractal's consensus algorithm over time.
Resources
- fractally White Paper
- Fractally White Paper Addendum 1
- Genesis Uncertainty Observatory
- Genesis Fractal Dashboard
- GitHub Repository with the Genesis Fractal Dataset
- First Results from the Fractal Governance Experiments
- On Simulating Fractal Governance
- Modeling and Simulation topic on gofractally.com
Updates
| Date | Description |
|---|---|
| 2022.07.26 | The plot titles and x-axis labels of figure 5, figure 6, figure 7 and figure 8 were clarified to use the words Accuracy and Precision instead of the words NominalValue and StdDev, respectively. |
Great work and great find on the value of attendance in the correlation between precision and accuracy
See my blog post where I outline how to measure group values and provide a critique to the methods described in this post: https://hive.blog/fractally/@dan/how-to-measure-consensus-on-group-values
Leaving my response to this article here for better visibility
https://james-mart.medium.com/re-a-model-independent-method-to-measure-uncertainties-in-fractal-governance-consensus-algorithms-e7ee7a47622d