But what does geometry have to do with daily life? Everything, according to experts, The creators of this science claim that geometry is the beginning of the mathematical era, this has been applied since ancient times in different cultures. " It's like a code where different patterns are used like art, architecture, music, regardless of latitude. It is a code of nature to create life, so much so that the body is built with geometric patterns and proportions, the plants also have a distribution and the heart, an internal coherence of electric waves in relation to those of the brain ", exist very important phrases that today are part of this science as for example.
The geometry has two great treasures, one is the Pythagorean theorem and the other the golden number, the first can be compared to a measure of gold and the second to a precious stone.
Johannes Kepler.
The geometry
Geometry (from Latin geometrĭa, and "measure") is a branch of mathematics that deals with the study of the properties of figures in the plane or space, including: points, lines, planes, polytopes (which include parallels, perpendiculars, curves, surfaces, polygons, polyhedra, etc.).
It is the theoretical basis of descriptive geometry or technical drawing. It also gives foundation to instruments such as the compass, the theodolite, the pantograph or the global positioning system (especially when considered in combination with mathematical analysis and especially with differential equations).

Allegory of geometry.
Its origins go back to the solution of concrete problems related to measures. It has its practical application in applied physics, mechanics, architecture, geography, cartography, astronomy, nautical, topography, ballistics etc. And it is useful in the preparation of designs and even in the elaboration of crafts.
History

Fragments of the Elements of Euclid in the Papyri of Oxyrhynchus.
Geometry is one of the oldest sciences. Initially it is constituted in a body of practical knowledge in relation to lengths, areas and volumes. The Babylonian civilization was one of the first cultures to incorporate the study of geometry. The invention of the wheel opened the way to the study of the circumference and later to the discovery of the number π (pi); They also developed the sexagesimal system, knowing that each year has 360 days, also implemented a formula to calculate the area of the rectangle trapezium.In ancient Egypt was highly developed, according to the texts of Herodotus, Strabo and Diodorus Sículo. Euclid, in the 3rd century BC C. configured the geometry in axiomatic and constructive form, a treatment that established a rule to follow for many centuries: the Euclidean geometry described in The Elements.
The study of astronomy and cartography, trying to determine the positions of stars and planets in the celestial sphere, served as an important source of resolution of geometric problems for more than a millennium. René Descartes simultaneously developed the algebra of equations and analytic geometry, marking a new stage, where geometric figures, such as flat curves, could be represented analytically, that is, with functions and equations. The geometry is enriched with the study of the intrinsic structure of the geometric entities that analyze Euler and Gauss, which led to the creation of topology and differential geometry.
Axioms, definitions and theorems
Geometry aims to go beyond what has been achieved by intuition. Therefore, a rigorous method is necessary, without errors; to achieve this, axiomatic systems have historically been used. The first axiomatic system is established by Euclid, although it was incomplete. David Hilbert proposed at the beginning of the XX century another axiomatic system, this one already complete. As in any formal system, the definitions, not only aim to describe the properties of objects, or their relationships. When something is axiomatized, objects become ideal abstract entities and their relationships are called models.
This means that the words "point", "straight" and "flat" must lose all material meaning. Any set of objects that verifies the definitions and axioms will also fulfill all the theorems of the geometry in question, and their relations will be virtually identical to those of the traditional model.
Axioms
In Euclidean geometry, the axioms and postulates are propositions that relate concepts, defined in terms of point, line and plane. Euclid posed five postulates and was the fifth (the postulate of parallelism) which centuries later, when many geometers questioned it when analyzing it, originate new geometries: the elliptical (Riemann geometry) or the hyperbolic Nikolai Lobachevski.
In analytical geometry, axioms are defined in terms of point equations, based on mathematical analysis and algebra. Acquire another new sense to speak of points, lines or planes. f (x) can define any function, call it straight, circumference, plane, etc.
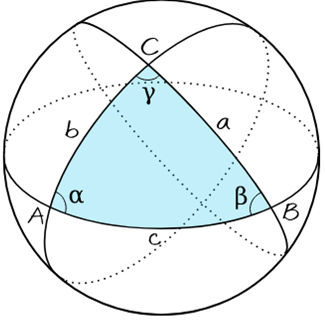
Spherical geometry is an example of non-Euclidean geometry.
Types of geometry
Since the ancient Greeks, there have been numerous contributions to geometry, particularly since the eighteenth century. This has led to the proliferation of numerous sub-sections of geometry with very different approaches. To classify the different developments of modern Geometry, different approaches can be used:
Geometries according to the type of space
The ancient Greeks handled a single type of geometry, namely, the Euclidean geometry, cleverly codified in the Elements of Euclid by an Alexandrian school headed by Euclid. This type of geometry was based on a formal style of deductions from five basic postulates. The first four were widely accepted and Euclid used them extensively, however, the fifth postulate was less used and subsequently several authors tried to prove it from the others, the impossibility of said deduction led to the observation that together with Euclidean geometry there were other types of geometries in which the fifth postulate of Euclídes did not participate. According to the modifications introduced in this fifth postulate, different families of geometries or different geometrical spaces are reached:
- The absolute geometry, which is the set of geometric facts derivable from only the first four postulates of Euclid.
- The Euclidean geometry, which is the particular geometry that is obtained from accepting the fifth postulate as an axiom. The Greeks considered two variants of Euclidean geometry:
- Euclidean geometry of the plane
- Euclidean geometry of space
- Classical geometry is a compilation of results for Euclidean geometries.
- From the XIX century, it was concluded that non-Euclidean geometries could be defined among them:

Teaching and learning geometry
The learning of geometry involves the development of visual skills and argumentation.
So that the learning of the geometry does not lack of sense, it is important that the educational group worries about looking for a balance between the association of skills of visualization and argumentation, since both skills are fundamental within the formative process of the individual. That is, it is not just about teaching content as a "recipe" or to comply with the stipulated in the curriculum, but it is intended that with the teaching of geometry the student learns to think logically.3
The human being, from his childhood, creates representations of the physical world that surrounds him. These generate a need (theoretical and practical) to achieve the understanding of that world. The right hemisphere of the brain is the most benefited in the presence of visual stimuli, unlike the left hemisphere, which has the responsibility to develop verbal abilities. The study of geometry contributes significantly to the development of those spatial visualization needs; however, until a recent historical period, dating from the decade of the 50s, is when mathematical educators were interested in the study of this field, linking the mathematical capacity with spatial capacity.
References
1 . Baldor, Gaaplex (2014). Plane and space geometry and trigonometry. Mexico: cultural publications. ISBN 978-8435700788.
2 . Wolchover, Natalie (September 17, 2013). «Physicists Discover Geometry Underlying Particle Physics | Quanta Magazine ». Quanta Magazine. Retrieved on February 20, 2017.
3 . Gamboa-Araya, Ronny; Ballestero-Alfaro, Esteban (2010). «The Students' Perspective of Geometry Teaching and Learning in High School». Electronic Journal Educare 14 (2): 125-142. ISSN 1409-4258. Retrieved on 2017-07-28.
4 . Gamboa-Araya, Ronny; Ballestero-Alfaro, Esteban (2010). «The Students' Perspective of Geometry Teaching and Learning in High School». Electronic Journal Educare 14 (2): 125-142. ISSN 1409-4258. Retrieved on 2017-07-28.
5 . Gamboa-Araya, Ronny; Ballestero-Alfaro, Esteban (2010). «The Students' Perspective of Geometry Teaching and Learning in High School». Electronic Journal Educare 14 (2): 125-142. ISSN 1409-4258. Retrieved on 2017-07-28.
Bibliography
- Boyer, C. B. (1991) [1989]. A History of Mathematics (Second edition, revised by Uta C. Merzbach edition). New York: Wiley. ISBN 0-471-54397-7.
- Nikolai I. Lobachevsky, Pangeometry, translator and editor: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society, 2010.
- Jay Kappraff, A Participatory Approach to Modern Geometry, 2014, World Scientific Publishing, ISBN 978-981-4556-70.
- Leonard Mlodinow, Euclid's Window - The Story of Geometry from Parallel Lines to Hyperspace, UK edn. Allen Lane, 1992.


This article is almost entirely a translation of the Spanish Wiki page https://es.wikipedia.org/wiki/Geometr%C3%ADa So you should already refer to this page in the beginning
Enjoy the vote and reward!
nice article