Wie funtionieren eigentlich Indikatoren? EWMA mit MATLAB und Python

Hallo steemit Community!

Seit ich angefangen habe, mit Cryptos zu traden und Teil der Community zu sein, beschleicht mich zunehmend das Gefühl, dass viele Leute nicht so recht wissen, was diverse Indikatoren eigentlich aussagen und wie diese wirklich funktionieren. Man beschränkt sich gern auf die praktische Nutzung, weil sie immerhin relativ gute Ergebnisse bringt. Dabei wird oft außer Acht gelassen, dass es in einem Bullenmarkt wie bei den Kryptowährungen tatsächlich schwer ist, kein Geld zu verdienen.
Ich perönlich finde hingegen, dass es durchaus sinnvoll ist, die Mechanismen hinter den Indikatoren zu verstehen, zumal sie von vielen Tradern täglich benutzt werden. Daher werde ich eine Reihe an Posts veröffentlichen, die sich mit deren Implementierung befasst.
Anfangen werde ich mit einem relativ einfachen Indikator, dem exponentially weighted moving average oder kurz EWMA. Bei Interesse seitens der Community werde ich gerne weitere Indikatoren beschreiben und Möglichkeiten der Implementierung zeigen.

Also, los geht´s!

Teil 1: Z-Transformation?

Grundsätzlich arbeite ich gerne mit Übertragungsfunktionen im Bildbereich. Um zu verstehen, worum es sich dabei handelt, führt kein Weg an der Z-Transformaion vorbei. Diese ist ein mächtiges Werkzeug zu Erstellung von Filtern und erspart einem eine Menge programmierarbeit, wenn man z.B. MATLAB oder Python verwendet. Genauer gesagt kann man mit ihr einen EWMA in drei Zeilen implementieren, siehe Teil 3.
Leider braucht es ein bisschen, um sämtlich Zusammenhänge vollständig zu verstehen. Wenn du also keine Lust auf stundenlange Lektüre hast oder in diesem Bereich bereits sattelfest bist, kannst du gleich mit dem nächsten Kapitel fortfahren. Auch ohne ein Verständnis der Hintergründe sollte die Implementierung intuitiv verständlich sein.
Anderenfalls sind hier ein paar Links zum Thema:

Das sehr gelungene Buch von Otto Föllinger:
https://www.amazon.de/Laplace-Fourier-z-Transformation-Otto-F%C3%B6llinger/dp/3800732572/
Weblinks:
https://www.acin.tuwien.ac.at/fileadmin/cds/lehre/aut/Archiv/WS1314/AnhangB.pdf
https://de.wikipedia.org/wiki/Z-Transformation

Teil 2: Eigenschaften des EWMA

Bevor wir anfangen, Code zu schreiben, sollten wir uns fragen, wodurch sich der EWMA auszeichnet. Dieser gewichtet, im Gegensatz zum simple moving average (SMA), zeitlich nähere Werte stärker. Genauer gesagt nimmt die Stärke der Gewichtung exponentiell ab.
Um eine Übertragungsfunktion bestimmen zu können, müssen wir uns überlegen, welche Impulsantwort einem EWMA entspricht. Unter der Impulsantwort versteht man die "Reaktion" eines Filters auf einen Impuls der Höhe 1.
Wenn man sich nun vorstellt, dass man unser Filter ein mal mit besagtem Impuls anregt, so kommt man zu dem Schluss, dass die Impulsantwort mit jedem Sample, um einen bestimmten Prozentsatz abnehmen muss. Exponentialfunktionen haben grundsätzlich die Eigenschaft, in einer bestimmten Zeit um einen bestimmten Prozentsatz zu steigen oder zu fallen. Das Sample an der Stelle n berechnet sich also zu:

$x[n]=x[n-1]*k$

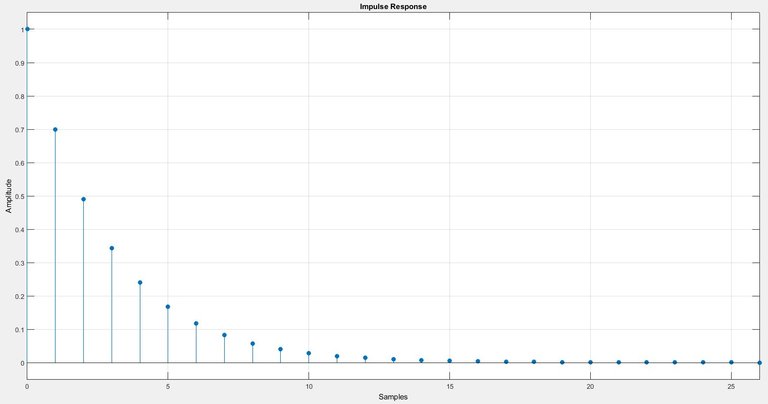
Als Beispiel sei hier die Impulsantwort eines EWMA-Filters mit k = 0,7 angeführt:

Wie man sieht, wird ein Sample gebildet, indem man das vorherige mit 0,7 multipliziert.

Wir wissen nun also, dass sich die benötigte Impulsantwort berechnet zu:

$h[n]=k^n$

Unter https://de.wikipedia.org/wiki/Z-Transformation#Tabelle_der_Korrespondenzen_der_zeitdiskreten_Funktionen findet man die zugehörige Z-Übertragungsfunktion:

$H(z)=\frac{z}{z-k}$

Grundsätzlich versteht man unter h[n] die Impulsantwort und unter H[z] die entsprechende Übertragungsfunktion.

Teil 3: Implementierung in MATLAB:

Hier beginnt sich das Erlernen der Z-Transformation auszuzahlen: Der Code für die Implementierung ist (abgesehen von der Funktionsinitialisierung) gerade einmal drei Zeilen lang!

function [ EWMA ] = EWMA( PriceVector, k )

a = [1 , -k];         %%Polstellen 
b = (1);              %%Nullstellen

EWMA = (1-k)*filter(b,a,PriceVector);

end

Mit den Vektoren a und b wird die Übertragungsfunktion bestimmt. Die Funktion filter wendet diese auf den eingehenden Vektor, also zum Beispiel die Preise des letzten Jahres, an.
Der Korrekturfaktor (1-k) ist nötig, da ohne ihn das Ergebnis falsch wäre: Man stelle sich die Überlappung der Impulsantworten der einzelnen Samples (auch Faltung genannt und von der Funtion filter durchgeführt) vor: Die Werte des EWMA wären viel zu hoch!

Teil 4: Implementierung in Python

import numpy
import scipy
import scipy.signal

def EWMA(self, PriceList,k):
        a = [1, -k]         #Nennerpolynom
        b = [(1-k)]         #Zählerpolynom (normieren der Summe der Impulsantwort)
        ic=scipy.signal.lfiltic(b,a,PriceList)
        result = scipy.signal.lfilter(b, a, PriceList, zi=ic)
        return result[0]

Wie man sieht, muss man in Python drei Bibliotheken einbinden. Weiters wird die Variable ic berechnet. Diese ist die Anfangsbedingung unseres Filters und kann in Python bequem mittels der Funktion scipy.signal.lfiltic bestimmt werden. Sie führt dazu, dass sich das Filter nicht erst einschwingen muss. Der Korrekturfaktor (1-k) ist diesmal im Zählerpolynom enthalten.
Der Vektor result beinhaltet die Berechnungsergebnisse, result[0] ist dabei das aktuellste.