RE: Daily Maths Problem #1

@grubbyhat is completely right about the answer being square root of two.

To understand this, note that there is a difference between the situation with a finite number of operations and an infinite number of them.

There's that joke about an infinite number of mathematicians who enter a bar. "One pint of beer please", asks the first. "Half a pint", says the second, "One quarter, please", goes the third, "STOP!", says the barman and pours 2 pints for everyone. _{(This is the point where you laugh)}

The reason for this joke is that you can actually totally seriously consider the value of an infinite sum of the following form:

1 + 1/2 + 1/4 + 1/8 + 1/16 + ....

Any finite part of this sum will always be smaller than 2, but as the number of terms approaches infinity, the sum will get arbitrarily close to 2. At this point mathematicians would say that the limit value at infinity is, in fact equal to two.

Still with me?

Now consider the question about x^(x^(x ...). What this expression essentially denotes is the limit of the following sequence of numbers:

x,
x^x,
x^(x^x),
....

If @grubbyhat wanted to be extra mathematically precise, he could have written the problem in the following form:

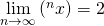
(where 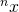denotes tetration, raising x to its own power n times, see this also).

It turns out that, indeed, if you choose root 2 for the value of x the corresponding limit will be equal to 2. You may check it numerically by increasing the number of terms and observing how the sequence approaches two.

To solve the problem, however, you do not even need to know much about limits. Instead simply observe that:

2 = x^(x^(x^ ....) = x^{x^(x^ ....)} = x²

Because the power that the very first x is raised to is the same infinite sequence itself.

So technically you do owe @grubbyhat a SBD.