Today on Legends Of STEM, we would be looking at the works of a man who is known to be amongst the early pioneers in the world of Science, he was an excellent mathematician, an Inventor and amongst all a thinker. Many know him for the word Eruka, an exclamation he made after one of his discoveries, he is worth the article.
Source: Commons
I can still go on with the introduction, but I think seeing his works will speak louder, so join me as we learn about the man, Archimedes Of Syracuse.
His Early Life
The Greeks are well known to have given science quite a push, they added to knowledge producing logical arguments which aided the advancement of Science and Archimedes was an addition to the great minds of the Greek.
He was quite a thinker Source: Wiki Common, Artist : Domenico Fetti
Born to the scientific culture of the Greeks in 287 BC , it was inferred from one of his work that his father was an astronomer. Most of his lifetime was spent in Syracuse but in his young age, he lived at the city of Egypt where the greatest library of his time was, this library was known to be where scholars of the ancient world meet.
His works were preserved in this library by Eratosthenes, a man in charge of this library, a man said to be the first to accurately calculate the size of earth.
His biography was written by a friend Heracleides but Is long lost hence not much about his life is known by us, information like if he did marry or had children are unknown, though many of his works were lost, some of his works were preserved which led to what we now know about the man Archimedes.
Are you a member of steemSTEM and have no idea of some of the Great works of Archimedes, this is a chance, join me as we explore some major works, you will be amazed at what the human brain can achieve and how great a man he was.
A LEGEND OF STEM
The Story Of Eruka
Before his time, there was known to be no way to measure the volume of an irregular solid, Archimedes not only discovered a way but also explained it clearly hence it became a base of measurement of volume, this is a story of Eruka.
A quantity of gold was given to a craftsman for use to bring to make a crown for the King of Syracuse, King Hiero II, the gold for the crown was supplied by King Hiero himself, and according to the words of the king, the crown was fabricated. After making this crown, it was said that it weighed the same as the gold supplied but the king was not convinced for he had a feeling that some amount of gold was stolen and replaced with silver, and our hero, Archimedes was to explain if his thoughts were true.
Gold was known to be denser than silver, but the big problem was that this crown was an irregular shape whose weight was known but volume unknown, hence to determine if it was of a truth made with all the gold supplied, since there was no means of measurement, it might employ a form of melting and accessing it's content but this had to be done without such destruction.
As he got into his tub to take his bath, the mystery behind the Archimedes principle surfaced. He took to notice that as he got in, there was a rise in water level in the tub and this was a breakthrough to calculate the volume or the irregular crown.
He was said to have ran the streets naked on his discovery, Eruka!!!,he cried Source: Wiki Common, Artist : Giammaria Mazzucchelli
Eureka!, Eureka!! (meaning, I have found it ) he cried in excitement running naked in the streets of Syracuse to make his findings known.
He explained that measuring the level at which water is displaced as an object sinks would tell if the crown was made of pure gold or mixed with silver, here is why, since the gold and silver are not similar in weight, you will need a larger volume of silver to bring a kilogram weight when compared to gold.
Hence if a pure gold of 1kg displace the water level by a certain height, the Kings crown if weight of 1kg would displace the water level by same height but if it weighs 1kg and displaces more than the measured height of 1kg, then some amount was replaced.
This brought to light that the crown was not made purely of gold but a mixture of silver and gold, quite a bad news for the craftsman and that was the brain of Archimedes at work.
The Archimedes Screw
The Archimedes screw is one of the major works by Archimedes in the field of engineering, this is a screw which is fitted into a hollow pipe, this screw can be turned by human Labour or any other means at one end while the other end is fixed in the liquid needed to be transported.
Turning of the shaft tend to scoop up an amount of liquid which is further moved upwards through the tube with respect to the rotating heliciod up until it reaches the top end.
For this to be achieved, there need no perfect contact between the pipe and screw since the water scooped with respect to the turning screw is more than that leaking out per turn, also water leak in an upper section is moved upwards by a lower section, quite brainy right?.
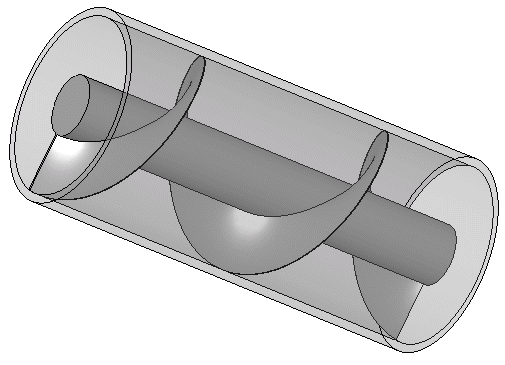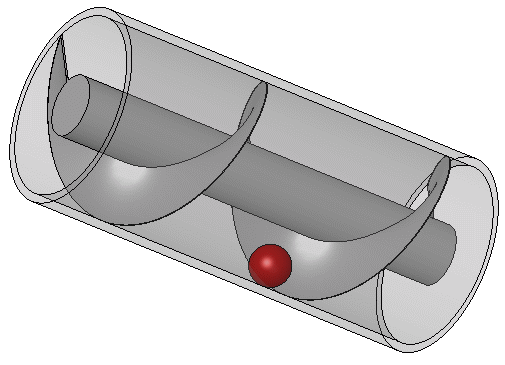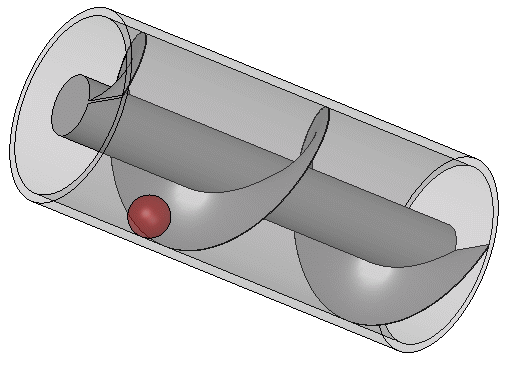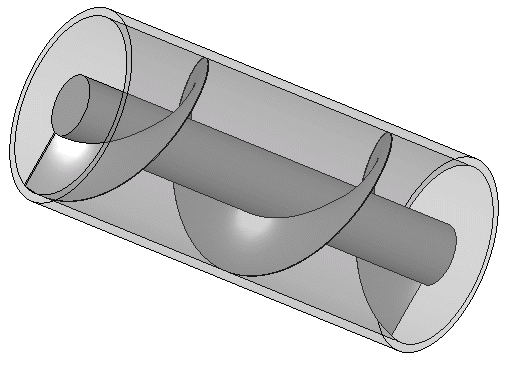Principle Of The Archimedes Screw, Author : Silberwolf This screw have a wide spread use In our world of today even on pumping liquids and the transfer of granular solids like grains and coal, and in 1839 the St Archimedes was lunched, this is the first ship with screw propeller and it was named in honor of the Archimedes Screw.
The Archimedes Claw
Syracuse was always at war and Archimedes had a part to play in its defence, the Archimedes claw also called the ship shaker was a weapon designed by Archimedes which was made up of an arm which is crane like when viewed and had a grappling hook made of metal which is suspended, ready for its prey.
On dropping the claws on any ship, the claw will swing in an upward direction hence it lifts the ship from the water and sinks it.
A guess illustration of the Archmedes claw
Experiments have been conducted with regards to the Archimedes claw and it has been proven to be a workable weapon.
Archimedes In Light
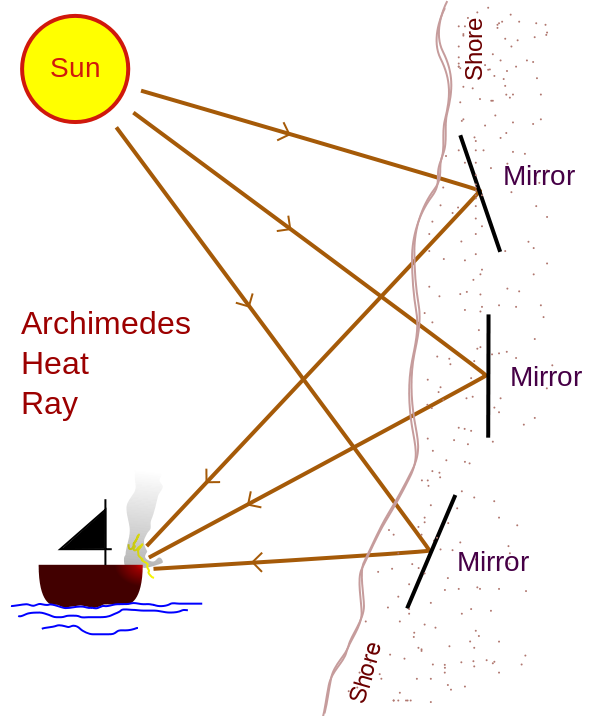
Records have it that our hero may have set ships on fire using mirrors used to reflect the rays of the sun collectively on a ship, Archimedes was quite a man of knowledge and this his weapon was referred to as the burning glass but some might also refer to this weapon as the Archimedes heat rat.
The Archimedes heat ray tries to focus the action of heat by reflection of light by fine surfaces and this intensity which consists of many reflection will was capable enough to set ablaze ships coming to attack Syracuse, some other device which are in relation to the Archimedes heat ray have been constructed in modern times and are now referred to as a solar furnace or a heliostat.
Although verification of this weapon of weather built by Archimedes is still a debate as it was rejected by Rene Descartes but recent times have seen researchers try to prove the existence of this weapon recreating the scenario using tools which is felt might have been available for him in his period, and the discovery was of its possibility as copper shields or a good polished bronze can perform such.
According to a test conducted in 1973 by a Scientist named Ioannis Sakkas in Athens, to set a typical Roman ship on fire, needed was about 70 mirrors which were made to reflect the rays of the sun to a plywood, on accurate focus, there were flames just in matter of seconds, as the Roman ships then were said to have been coated with tar, aiding the combustion.
When this experiment was later conducted by some students of Massachusetts Institute of Technology, on a ship made of wood, fire was observed to break out but this was on conditions that the ship must be stationery for about ten minutes of focus, hence conclusions were made that our hero Archimedes might have designed such.
Approximating The Value Of PI ( π )
Mathematicians know the pi as that gotten when the circumference of a circle Is divided by its diameter, hence in the calculation of the area of a circle, the value of pi is quite important but how can this be done if there is no approximate value for its value.
Archmedes was known to be a man so much interested in the calculation of properties of solid shapes and when he came across curved solid shapes, he needed to know more about the value of pi. We know this value to be an irrational number with with a never ending pattern after its decimal Place, but an exact value was needed.
Below is a view of how he did this.
A circle was imagined and an equilateral triangle drawn inside of it with each edge of the triangle touching the circle, outside of the circle, another triangle of same shape was drawn but this time it's sides were made to touch the curves of the circle, and this was all a mental image.
Doing this, the parameter of each triangle can be easily calculated and hence logically, it was known that the circumference of the circle is now bounded to fall in the range of either being greater than the triangle drawn inside and also less that the triangle drawn outside the circle.
Now it's time to reduce this boundary, because it seem quit large for the circumference, and what better way to do this than using a polygon. A hexagon was further drawn inside the circle and outside too and this time it was more enclosed when compared to the triangle bringing it a bit nearer to the circles circumference, hence the limit of maximum and minimum with regards to the circumference of the circle was further tightened.
And this was continued with a polygon of twelve sides, followed by 24, 48 up until he bounded this circle by a 96 side polygon both inside and outside of the circle.
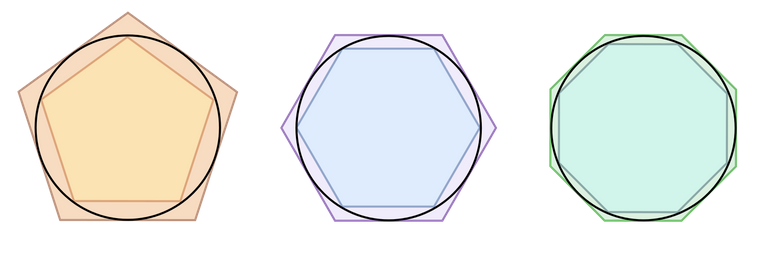
From triangles to polygons of many sides
When drawn, this gives an approximate circle which was used for the estimation of the value of pi, hence the value was estimated to be greater than 310⁄71 and less than the number 31⁄7 hence a limit average of 3.141868115 and this value of pi was extensively used up to the emergence of the digital age.
Calculating The Volume Of A Sphere
He was a man with quite an imaginative mind, fascinated by curves he took the challenge for the volume of a sphere and emerged the first to explain a method to get the total volume of a sphere an it was quite a method he developed which confirmed him to be one of the greatest mathematician when compared to many in his time.
Unlike the surface of a cube which changes with respect to covers and edges, the surface of a sphere is changes with respect to direction making it incredibly hard to figure out a way to calculate it's volume and this was what our hero was all about, tactical.
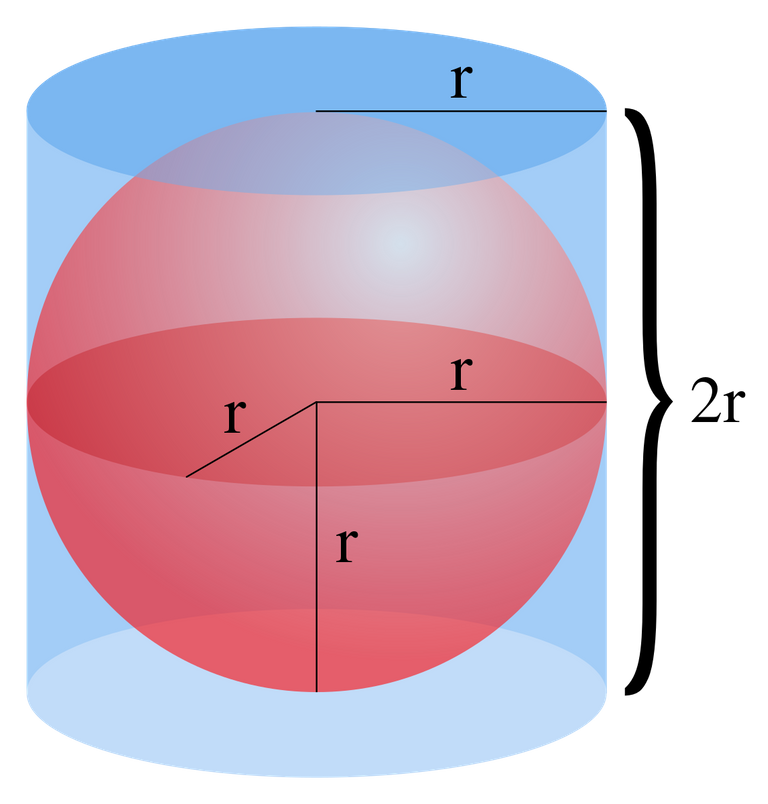
The Archimedes sphere in cylinder to determine the volume of a sphere
To get this, Archimedes first imagined cutting this sphere into half, two hemispheres, he took one which gave a flat surface under to begin with, and finding the volume of this hemisphere when multiplied by two, gives the total volume of the sphere.
Placing the hemisphere on a flat surface, he imagined a cylinder fitted around the hemisphere, hence a the diameter of the cylinder is the same as the diameter of the base of the hemisphere and also the height of the cylinder was the same as the height of the hemisphere, then the brain work began.
Archemedes began cutting with his mind slices from the top of the cylinder, these slices were cut horizontally and through the cylinder and the hemisphere, and at the top of the cylinder, the hemisphere was at its smallest shape, a view from the top will show a small diameter hemisphere.
He continued with the slice, and this time, he went a bit lower from the top, when viewed from the top, it's noticed that the cylinder circle remained at same diameter while the circle of the hemisphere was seen to have got a little larger and this, he continued downward moving bit by bit until the cylinder circle was now the same size with the hemisphere circle.
When he took these cuts, the heights were put into consideration and he got these slices as many as possible and as thin as he could, he then took to note the area of each of parts in form of rings which were not covered by the hemisphere during the cut and these rings when multiplied by their small Heights were discovered to give the volume of the parts not filled by the hemisphere.
On doing this, he discovered that the volume gotten equal the volume of a cone of base that of the radius of the height same with that of the cylinder used, hence, the volume of the hemisphere equals the volume calculated cylinder volume minus the volume of cone gotten.
As known, the volume of a cylinder is πr2h and that of a cone is 1⁄3πr2h in the illustration the height equals the radius hence volume becomes πr3 and 1⁄3π r3 and a subtraction will give the volume of the hemisphere of this cone as
V = 4⁄3πr3
Quite a Brainy man don't you agree.
Other Notable Works By Archimedes
Equilibrium Of Planes: Though the principle of the lever was not enacted by him, in two of his books, he tries to explain it's principles, saying that two magnitudes are in a state of equilibrium at a distance which are reciprocal promotional to each of their weights. This principle was also used to calculate the center of gravity and areas of some geometric figures.
Floatation : Amongst other works by Archimedes in Floatation, he brought about the principle of buoyancy also known as the Archimedes principle which states that
A body wholly or partially immersed in a fluid experience an upthrust, equal to but opposite in sense to the weight of the fluid displaced.
The Beast Number : Initially the Greek number was used and this number was limited, Archimedes wanted a number which can be able to equal the number of sand in a beach, he needed something enormous which was not only able to count how many grain of sand there were in a beach but capable of numbering the numbers there were in the universe, hence the beast number (as called) was introduced.
The Beast Number makes use of what we now refer to as exponents or index numbers, back then 10^4 was called a myriad which is ten thousand. Archimedes referred to it as the
myriad-myriad units of the myriad-myriadth order of the myriad-myriadth period.
And you would ask, what can the number really be used for, actually let's try to write write the diameter of the earth in centimeters, hmm, we might need something quite close to Archimedes beast number.
How brainy can this get, Smiles
N/B: Listed here are major works which he was known for, for further reading of the works of Archmedes, see text sources below *
Death And Legacy
Archimedes died in 212BC after the capture of the city of Syracuse by the Romans which took a siege that lasted two years. Many stories were told of how he died one of which he was contemplating on a mathematical drawing and was commanded to come meet the General which he refused on grounds that he had a work to complete and was killed by the enraged soldier.
An art illustrating a proposed death, though unknown to us
Another account was that he died trying to surrender to the Roman soldier and his mathematical instruments were either considered valuable items or weapons, but reports had it that the General was angered on his death as he had given commands to keep him alive being considered a great scientific asset.
Archimedes was quite a blessing to our world a man of value who contributed a lot which helped this world of innovations, Galileo called him a superhuman and many sang of his praises, a crater was kept on moon and the lunar mountain and was tagged Archimedes in honor of his works. Eureka! is now the motto of California but this was when gold was found close to Sutter's Mill which inspired the California Gold Rush.
Would we get a man like him again, only time only time will tell, do you want to be the Archimedes of our time?, that's quite achievable if you ask me, am waiting to hear of your first invention, and will be so pleased to feature you in a Legend of STEM article.
So keep up the great works, keep it coming, it's only Logical.
You probably might have missed this article :
LEGENDS OF STEM - LEONARDO DI SER PIERO DA VINCI
That's another man to learn about
Until Next Time, Think Logical
REFERENCES
Images
All images are sourced just below them.
Thanks for the appreciation given :) , keep up the good work.