Hi everyone. This math post is on combinations. The contents of this post is intended for middle school students. A natural extension would be to talk about sets, Cartesian products and some of its uses in programming (data science, computational statistics). The word combination is used loosely here.

Topics
- What Is A Combination?
- Combination Examples
- Notes
What Is A Combination?
A combination is a selection of items from a collection. This selection of items is not in a particular order. An ordered selection of items in mathematics is called a permutation and that is a different topic.
Combination Examples
Example One - Desk & Chair
You go to your nearest IKEA store and want to buy a desk and a chair. This desk and chair combo is for a home office or gaming studio. Desk sizes are either small, medium or large. Chair types are either comfortable or stylish.

| Desk Size | Chair Type |
|---|---|
| Small | Comfortable |
| Medium | Stylish |
| Large |
What are all the ways (combinations) of getting a desk and chair?
If we have a small desk, we can get a comfortable chair or a stylish chair. We get two ways from the small desk which are a small desk and a comfortable chair and the second one being a small desk and a stylish chair.
Given a medium sized desk, we can get a comfortable chair or a stylish chair. There are another two ways here.
With the large desk size, it is similar to the first two cases.
Listing out all the ways of getting a desk and chair looks like the table below.
| Combination Number | Desk Size | Chair Type |
|---|---|---|
| 1 | Small | Comfortable |
| 2 | Medium | Comfortable |
| 3 | Large | Comfortable |
| 4 | Small | Stylish |
| 5 | Medium | Stylish |
| 6 | Large | Stylish |
An alternate table can be arranged like the one below.
| Combination Number | Desk Size | Chair Type |
|---|---|---|
| 1 | Small | Comfortable |
| 2 | Small | Stylish |
| 3 | Medium | Comfortable |
| 4 | Medium | Stylish |
| 5 | Large | Comfortable |
| 6 | Large | Stylish |
Regardless of which table format that is chosen, you can see that the number of ways of choosing a desk and table is six. This is from three multiplied by two.
Example Two - Choosing School Courses
A math major at a small college is choosing 5 courses for her first semester. Three of the five courses are mandatory and the last two courses are elective courses from a list of five language courses.
The three required courses for the semester are:
- Linear Algebra I
- Calculus I
- Introduction To Mathematical Proofs
Elective options include:
- French I
- German I
- Spanish I
- Arabic I
- Italian I
What are all the different set of courses for the semester?

Since the three math courses are required, those choices are already set. What is of interest is choosing the different arrangements of the two language courses as electives.
Note that the order does not matter for course number. Having Calculus I as course one and French I as course 5 is the same as having French I as course I and Calculus I as course five for example.
| Course 1 | Course 2 | Course 3 | Course 4 | Course 5 |
|---|---|---|---|---|
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | French I | German I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | French I | Spanish I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | French I | Arabic I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | French I | Italian I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | German I | Spanish I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | German I | Arabic I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | German I | Italian I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | Spanish I | Arabic I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | Spanish I | Italian I |
| Linear Algebra I | Calculus I | Intro. To Mathematical Proofs | Arabic I | Italian I |
There are 10 different arrangement of courses for a semester given the choices.
Imagine a regular university with about 12 departments where each department offers about 20 choices. The number of arrangements would be massive (even with time restrictions as you cannot have two classes at the same time).
For more technical people, the 10 arrangements comes from 5 choose two or 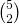 .
.

Example Three - Make Your Own Ice Cream Cone
A very small local ice cream shop offers ice cream with these choices.
| Cone Size | Number Of Scoops | Flavours | Toppings |
|---|---|---|---|
| Regular | 1 | Vanilla | Sprinkles |
| Large | 2 | Strawberry | Chocolate Chips |
| - | 3 | Chocolate | Marshmellows |
a) How many different ice cream cones can you make?
b) If the ice cream store ran out of chocolate flavoured ice cream, how many ways can you make an ice cream cone?
c) Suppose a new mango flavour was added as a flavour on top of the table above. (Don't remove chocolate.) How many more ways can you make an ice cream cone?

Answer To a)
For cone sizes there are two sizes. With the number of scoops there are three choices. For flavours and toppings there are three choices each. Multiplying the number of choices from each selection category gives 2 x 3 x 3 x 3 = 54. There are 54 ways to make your custom ice cream from this small ice cream place.
Answer To b)
No more chocolate ice cream cuts the amount of flavours from three to two. Multiplying the number of choices from each selection category now gives 2 x 3 x 2 x 3 = 36. With the chocolate flavour no longer available there are 36 ways to design your ice cream cone.
Answer To c)
Adding a new flavour such as mango increase the number of flavours from 3 to 4. There are now 72 ways to design an ice cream cone. (This is from 2 x 3 x 4 x 3 = 72.)

Notes
Arrangements, combinations do appear often in real life. Other examples include custom pizzas, custom sandwiches, custom-made clothing, choosing your outfits.
The examples in this post are small. Imagine the amount of combinations in a larger ice cream shop or at Blaze Pizza.
For programmers (data science in particular), there are times where there are table with combinations to work with.
In the area of statistics, there are two by two table, confusion matrices, hypothesis testing tables (Type I and Type II errors) for comparing decision making (accept/reject null hypothesis or predict this or that) versus actual outcomes.

I feel like the ideas here were not taught very well back in school along with probability.
!discovery 37
You bring up a good point. This gave me an idea for an education (math) post.
Looking over some of your past posts, feel free to re-post a couple of your favorites to the Mathematics community
Sounds good.
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
This post was shared in the Curation Collective Discord community
community witness. Please consider using one of your witness votes on us here for curators, and upvoted and reblogged by the @c-squared community account after manual review.@c-squared runs a
Congratulations @dkmathstats! You received a personal badge!
You can view your badges on your board And compare to others on the Ranking
Support the HiveBuzz project. Vote for our proposal!