Hi there. In this math post, I go over some examples of solving problems involving geometric sequences.
Math text images rendered with QuickLaTeX.com

What Is A Geometric Sequence?
A geometric sequence of numbers is an ordered list of numbers. This ordered list of numbers is in such a way where the next number is a multiple of the previous number. All the numbers in this ordered list share a common multiple called a common ratio.
Examples of geometric sequences include:
2, 4, 8, 16, 32, ... where the common ratio is 2 as the next term is double of the previous term.
1, 0.1, 0.01, 0.001, ... where the common ratio is 0.1 or one-tenth.
This sequence of -1, +1, -1, +1, -1, +1 includes alternating signs -1, +1, -1, +1, ... where the common ratio is -1.
Geometric sequences can have a limited number of numbers (terminating sequence) or can never ending resulting in an infinite number of terms. (If you want to get more technical, the sequence diverges.)
The Geometric Sequence Formula For Finding The n-th Term
Given a geometric sequence of numbers, you have the following pieces for finding the n-term in the geometric sequence
- The first term
- Common ratio
- Number of terms
To find the n-th term in a geometric sequence, you can use the formula:


Problem Solving Examples - Finding The n-th Term
Example One
Given a simple geometric sequence of 10, 20, 40, 80, 160, ... what is the twentieth term of the sequence?
The first term is 10 and the common ratio is 2 (from 20 divided by 10, or 160 divided by 80). Since the question is asking for the twentieth term the variable n is 20.

Example Two
What is the tenth term in the geometric sequence of 1, 0.5, 0.25, 0.125, 0.0625, ... ?
The first term is 1 and the common ratio is 0.5 or half (from 0.5 divided by 1). Finding the tenth term involves using n = 10. It may be easier to use the fraction version of the decimal numbers in the sequence.

Problem Solving Example - Finding The First Term
A geometric sequence has five terms where the common ratio is 3 and the eighth term is 324. What is the first term?
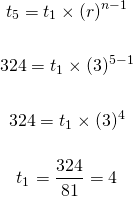
The first term of this particular geometric sequence is 4.
Problem Solving Example - Finding The Number Of Terms
A geometric sequence with a common ratio of 2 starts with 0.5 and ends with 1024, how many terms are there in this geometric sequence?
Start with the geometric sequence formula:

Substitute the known values into their respective variables. The unknown variable here is n in which we are trying to solve for.

Note that 2048 is two to the power of eleven.

Matching the exponents gives 11 = n - 1 which results in the number of terms (n) being 12.
Alternatively, you can use logarithms to solve for n:
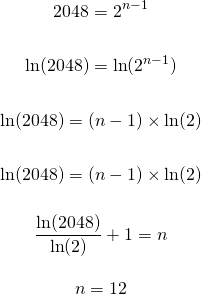

Problem Solving Examples - Finding The Common Ratio
Example One
The first term of a geometric sequence is 3 and the eighth term of this sequence is 384. What is the common ratio here?
With the geometric sequence formula, the unknown here is the ratio r.

Example Two - Money Example
Suppose you invest $1000 into a savings account with an interest rate compounded annually. After five years, this initial $1000 compounds into $1610.51 after five years. What is the interest rate?
In the finance context, the formula here is similar to the geometric formula. We have:

where:
- FV is the future value of the investment,
- PV is the initial investment at time 0
- r is the interest rate for the investment
- t is the number of years for this case.
(In general, t is the number of compound periods but that is beyond the scope for here.)
Substituting the known values and solving for the interest rate r gives:
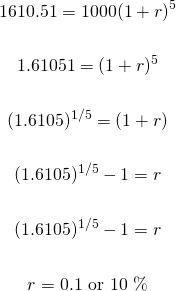

An Unusual Example
This particular example assumes the reader knows how to solving system of equations and is comfortable with (high-school) algebra.
Given a geometric sequence of three numbers which consists of -8, the square root of x and -72, what is the value of x and what is the value of the second term?
With 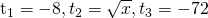 , you can set up two geometric sequence equations in this fashion.
, you can set up two geometric sequence equations in this fashion.

Substituting values gives these two equations:
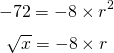
Solving for r in the second equation gives:

Substituting this r value into the first equation gives:
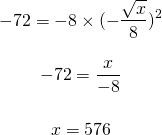
The value for x is 576 which means that the second term is the square root of 576 which turns out to be 24. This geometric sequence turns out to be -8, +24, -72. One neat thing about the problem is that we did not need to find the ratio to solve this question. (The common ratio here is -3.)

One of my big ah ha moments in maths was, the geometric series 1/2^n.
I loved the graphical illustration were you can see it adds to 1.
Nice Post keep it up