In this video I solve the quadratic equation by completing the square to obtain the famous quadratic formula. I had done a similar video 13 years ago so I thought it was time to do an updated one. Completing the square involves working backwards from the quadratic equation to obtain a form that has a square, that is of the form (x + d)2. From here we can take the square root and rearrange to solve for x, which obtains 2 values because of the nature of the square root.
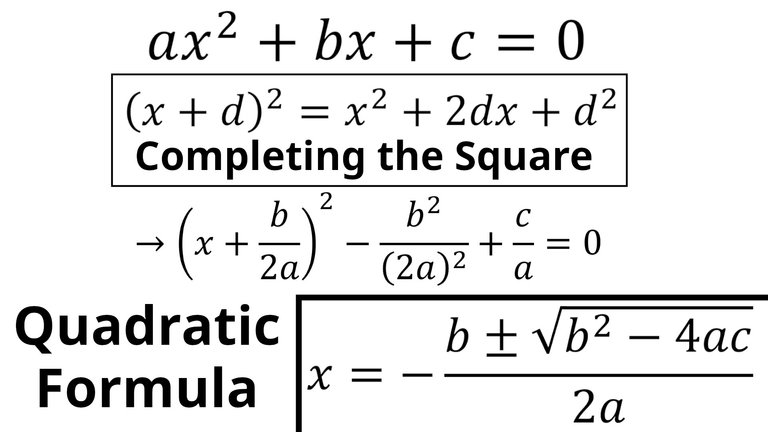
Time stamps
- Recap on Quadratic Formula: 0:00
- Derivation by completing the square: 0:30
- Completing the square: 1:16
- Quadratic equation as a square: 2:46
- Obtaining a common denominator: 4:25
- Quadratic formula: 5:58
Notes and playlists
- Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EF05ExjzLbB64NgUjoV1hl
- Notes: https://peakd.com/hive-128780/@mes/dzekfnxh
- PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIjYlhWw4dLq59fn0Xwg .
Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join
DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate
SUBSCRIBE via EMAIL: https://mes.fm/subscribe
MES Links: https://mes.fm/links
MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes
Email me: [email protected]
Free Calculators: https://mes.fm/calculators
BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm
Free Online Tools: https://mes.fm/tools
iPhone and Android Apps: https://mes.fm/mobile-apps
▶️ 3Speak
!summarize
Part 1/5:
Understanding the Quadratic Formula
In the world of algebra, few equations are as pivotal as the quadratic equation. It takes the form of ( ax^2 + bx + c = 0 ), where ( a ), ( b ), and ( c ) are constants, and ( x ) represents the unknown variable we want to solve for.
The overarching goal is to determine the values of ( x ) that satisfy this equation. By using the quadratic formula, the roots (or solutions) of the quadratic equation can be succinctly expressed as:
[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
]
This formula is derived through a method known as completing the square.
Revisiting the Derivation
Part 5/5:
With this fresh perspective, the quadratic formula remains an essential tool in tackling various equations across different fields of study, unlocking the mysteries of parabolic relationships inherent in mathematics.