Cubic Formula Proof Step 2: Applying Vieta's Substitution to Obtain a Quadratic Equation

[mes]

▶️ Watch on 3Speak

---

In this video I go over the second step in deriving the Cubic Formula, and this involves converting our earlier PQ version of the cubic formula into a quadratic formula using Vieta's substitution. In step 1 we converted x into y by the equation x = y + k. In step 2 we convert y into z by the equation y = z + k/z. Then we do the exact same procedure as before to select a k value that cancels out the z¹ terms. Then, multiplying by z³ we obtain a quadratic equation, which we can solve using the PQ version of the quadratic formula. In later steps, we will convert z back into y and then finally back into x.

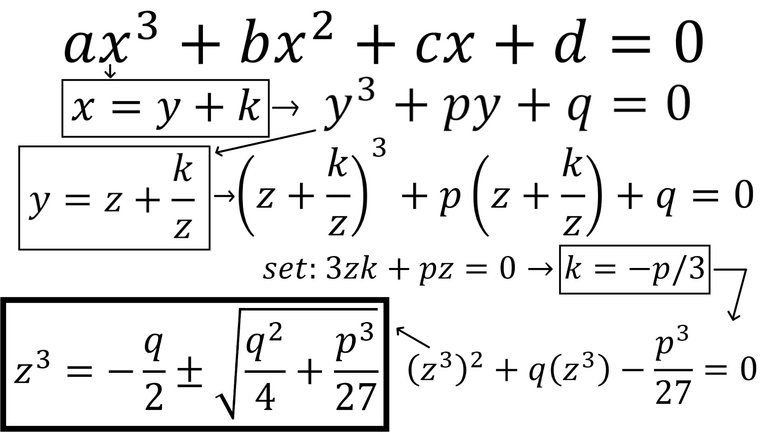
Timestamps

• Step 2: Solve PQ Cubic Equation using Vieta's substitution to obtain quadratic formula: 0:00
• Let y = z + k/z: 0:57
• Select k to cancel out z terms: 3:07
• k = -P/3: 4:13
• Convert resulting equation into a quadratic equation by multiplying by z³: 6:54
• Recall PQ version of the Quadratic Formula: 7:54
• Apply the PQ quadratic formula to our equation: 9:51
• Solution for z³: 10:58

Notes and playlists

• Summary:
• Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EF05ExjzLbB64NgUjoV1hl
• Notes: https://peakd.com/hive-128780/@mes/dzekfnxh .

---

Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join

DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate

SUBSCRIBE via EMAIL: https://mes.fm/subscribe

MES Links: https://mes.fm/links

MES Truth: https://mes.fm/truth Official Website: https://MES.fm Hive: https://peakd.com/@mes

Email me: [email protected]

Free Calculators: https://mes.fm/calculators

BMI Calculator: https://bmicalculator.mes.fm Grade Calculator: https://gradecalculator.mes.fm Mortgage Calculator: https://mortgagecalculator.mes.fm Percentage Calculator: https://percentagecalculator.mes.fm

Free Online Tools: https://mes.fm/tools

iPhone and Android Apps: https://mes.fm/mobile-apps

---

▶️ 3Speak

Comments

[mes]

!summarize

[hivebuzz]

Congratulations @mes! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)

You got more than 5500 replies. Your next target is to reach 5750 replies.

_{You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word STOP}

Check out our last posts:

	Our Hive Power Delegations to the January PUM Winners
	Feedback from the February Hive Power Up Day
	Hive Power Up Month Challenge - January 2025 Winners List