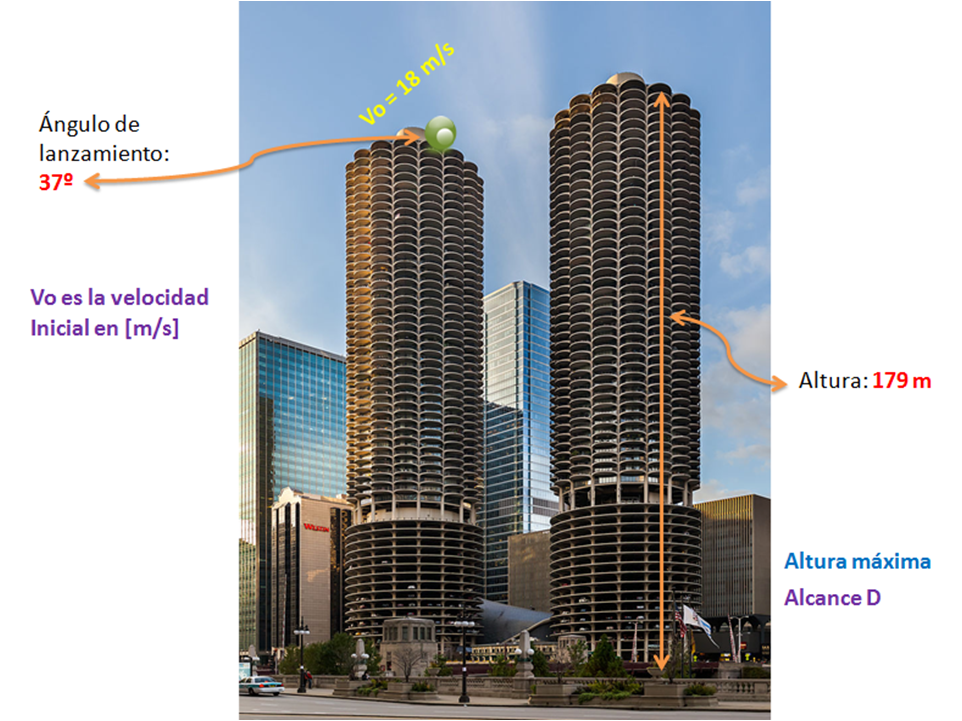
Tomaremos como referencia la azotea del Edificio Marina City Allí me ubico con la bola de billar que lanzaré a mi amigo Antonio que se posiciona en un borde de la azotea del edificio del lado derecho. Entre estos dos puntos de referencia existe una
, ¿la cuestión es estudiar la posibilidad que cuando lance esa bola, tenga la suficiente velocidad para que alcance el otro edificio y que sea atrapada por Antonio.
La Física Clásica se encarga de proponer varias ecuaciones que analizan la Cinemática de los objetos que se mueven en 1D, 2D y 3D en cualquiera de estos planos de referencia, en particular con el movimiento parabólico, se estudia como un problema combinado de 2 dimensiones, con un movimiento rectilíneo uniforme en el plano horizontal, donde la velocidad se mantiene constante durante todo el movimiento, Vx = constante [m/s], por supuesto que no hay aceleración que intervenga. Mientras que en el plano vertical intervendrá la aceleración de la gravedad (g = 10 m/s2), usaremos este valor para facilitar los cálculos, aunque el valor aceptado a nivel de la superficie terrestre es 9,80665 m/s2. En este caso, el cuerpo será atraido hacia el centro de la Tierra y caerá al suelo en algún intervalo de tiempo, por lo que se deberá tener presente el concepto de tiempo de vuelo tv

Los cuestionamientos invaden mi mente, las dudas en este tipo de movimiento son: (a) ¿cuál es la velocidad inicial que debo aplicar para que la bola de billar llegue justo a ese punto y no antes, porque caería al suelo? y (b) ¿con qué grado de inclinación la lanzo?, ya probé que si lo hago con 90º caería nuevamente en mis manos. Si la envío con mayor velocidad final me temo que pueda sobrepasar el edificio. El miedo y pánico al imaginar estas situaciones las pude ir liberando al encontrar algún soporte técnico y práctico en la aplicaciones del PhET Interactive Simulations
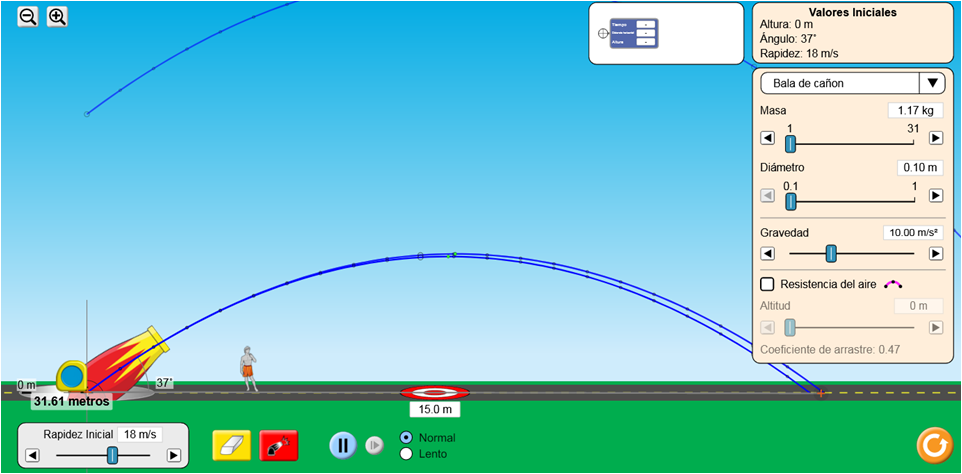
| Nota explicativa: el sistema de referencia no cambiará mi perspectiva del lanzamiento parabólico, así que he supuesto un punto de llegada en el suelo, ubicado a 25 metros, el color de la bola de billar y su masa no son datos relevantes para realizar los cálculos, siempre y cuando se desprecie la influencia del roce del aire. Estos detalles sí son considerados durante el vuelo comercial entre dos ciudades cualesquiera, pues un viento a favor o en contra de la dirección del desplazamiento va a afectar su velocidad de vuelo y finalmente influye en el tiempo de vuelo. |
Usaremos los datos que disponemos:
| Alcance [m] |
Aceleración g [m/s2] |
Velocidad inicial [m/s] |
Ángulo de tiro [º] |
| 15 |
10 |
18 |
37 |
Prácticamente disponemos de todos los datos iniciales y hasta más detalles del lanzamiento parabólico, así que vamos a aplicar las ecuaciones de este tipo de movimiento en dos dimensiones y verificar si la distancia horizontal (el alcance D, es el óptimo).
D = Vo2×Sen(2θ))/g
D = ((18 m/s)2×Sen(2×37º))/10 m/s2
D = 31,1 m

Haciendo los cálculos con las ecuaciones propuestas, vemos que el alcance es hasta 2 veces la separación entre las azoteas de los edificios gemelos, por lo que se supone que debemos disminuir la velocidad inicial o lanzar la bola con otro ángulo de inclinación. Ya pasé el primer susto, al sobrepasar a mi amigo Antonio y menos mal que no quedé corto con el lanzamiento porque habría entrado por una de las ventanas de algún apartamento o peor, rebotar hasta el piso del edificio sin saber si había alguna persona abajo. Ya tendré más cuidado y seguiré realizando cálculos apoyados en las ciencias físicas.
En la captura de pantalla se observan dos trayectorias parabólicas, pues supuse 2 valores de g = 9,8 m/s
2 y g = 10 m/s
2, como el parámetro g aparece en el denominador, al aumentar ese valor, el alcance D será menor, pasando de 31,8 m a 31,1 m, respectivamente. El valor que aparece cerca del cañón D = 31,61 metros es aproximado con el uso de la cinta métrica.
D = Vo2×Sen(2θ))/g
D = ((9 m/s)2×Sen(2×37º))/10 m/s2
D = 7,8 m
Al disminuir la velocidad del lanzamiento hasta la mitad, recorrerá la mitad de la separación entre los edificios, así que realizaré el tercer intento cambiando la inclinación del lanzamiento hasta θ = 18,5º, es decir a la mitad del valor original que había sugerido.
D = Vo2×Sen(2θ))/g
D = ((18 m/s)2×Sen(2×18,5º))/10 m/s2
D = 19,5 m
Ya me estoy acercando a que la bola llegue a las manos de Antonio. Sin embargo, no existe una forma directa de obtener los valores ideales, ya que a pesar que tenemos el resultado final del alcance D = 15 m y el valor de la aceleración de la gravedad, se requiere al menos una tercera variable de entrada conocida.
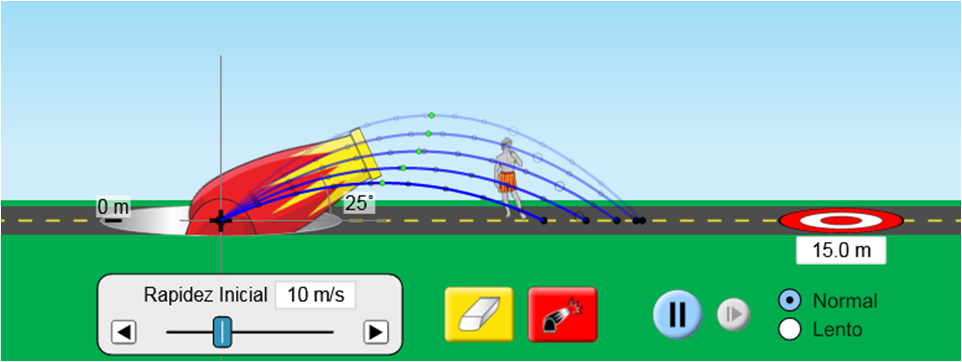
La experiencia con este tipo de simulación será el análisis del alcance con el ángulo de lanzamiento, para una velocidad inicial de tiro V
o = 10 m/s.
Para calcular el tiempo de caída usaremos los datos que disponemos:
| Velocidad inicial [m/s] |
Aceleración g [m/s2] |
Ángulo de tiro [º] |
Alcance [m] |
| 10 |
9,8 |
80 |
3,49 |
10 |
9,8 |
70 |
6,56 |
| 10 |
9,8 |
60 |
8,84 |
| 10 |
9,8 |
50 |
10,05 |
| 10 |
9,8 |
45 |
10,20 |
| 10 |
9,8 |
40 |
10,05 |
| 10 |
9,8 |
30 |
8,84 |
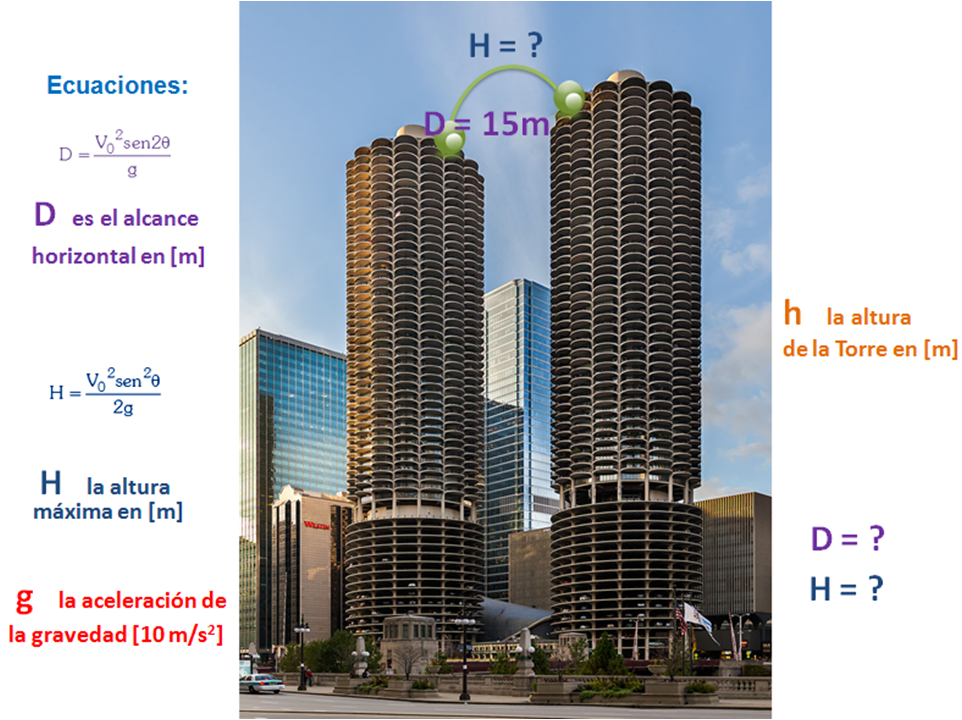
Lo primero que noto atractivo es que se llega a un valor máximo del alcance para θ = 45º, siendo simétricos para otros ángulos, siendo que el seno varía entre 0 y 1. Si había variado de 10 grados en 10 grados, me dibujaba solamente 5 trayectorias.
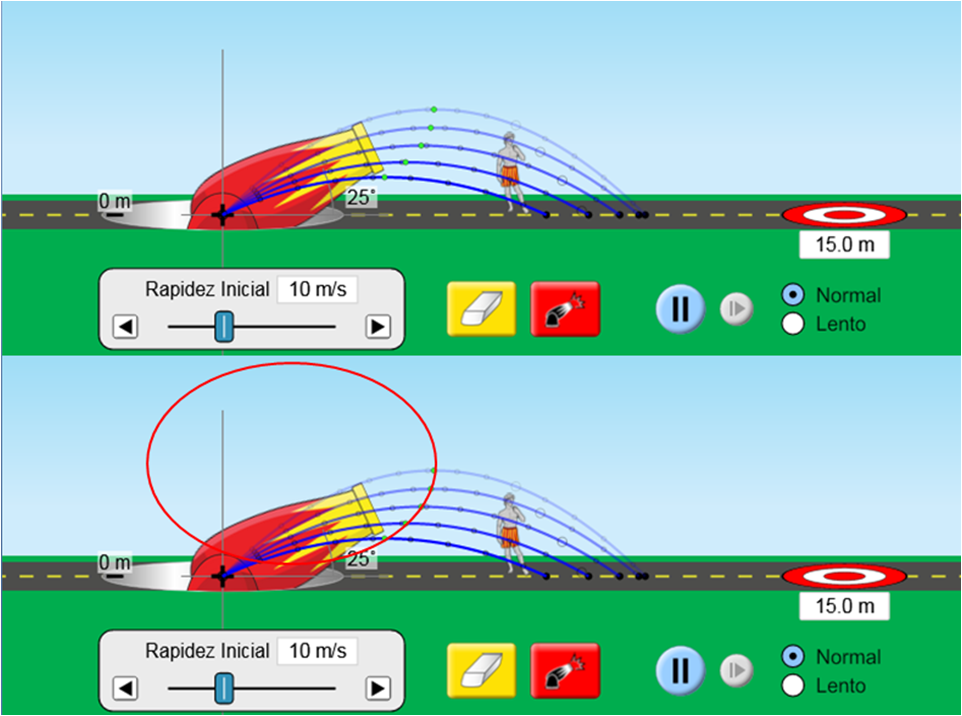
Otro detalle interesante es que los puntos de altura máxima alcanzada en cada uno de los lanzamientos anteriores y que están indicados por un punto de color verde en cada parábola es parte de una elipse centrada en X = 0, Y = V
o2/4g
| Con este valor de velocidad inicial Vo = 10 m/s, se supone que la bola de billar no pasará los límites de esta elipse, formando parte de una elipse de seguridad, por lo que había comentado antes, si es que había un techo o cuerdas sobre el punto de lanzamiento. |
Un supuesto válido para este lanzamiento es saber distinguir los puntos claves, como que la
máxima distancia horizontal se logra cuando el ángulo de tiro es de θ = 45º, así que jugaremos con los valores de la velocidad de lanzamiento, encontrando un valor aproximado de V
o = 12 m/s y de esta manera mi amigo Antonio tendrá su bola de billar para iniciar el partido con sus amigos y yo no tendré problemas con algún residente del edificio por vidrio roto o que le golpee a algún transeúnte.
Aporte del Post
Es cierto que las bases científicas de la Física se pueden aplicar a situaciones reales y que aplicando las ecuaciones planteadas en cada rama de ella, podemos resolver lo más mínimo de sucede en nuestro entorno, como sistema de referencia y considerando los parámetros físicos que podamos medir (tiempo, velocidad, temperatura, ángulos, distancias, etc.) |
Texto original de @azulear
Si deseas profundizar tus conocimientos acerca de este
tema, te recomiendo:









Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail., apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Congratulations @azulear! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 43000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts:
Support the HiveBuzz project. Vote for our proposal!